单频GPS基线精化解算的经验模式分解方法

范 千,方绪华,许承权

(1.福州大学土木工程学院,福建福州 350108;2.东华理工大学江西省数字国土重点实验室,江西抚州 344000;2.闽江学院地理科学系,福建 福州 350108)

对于单频GPS短基线,采用相对定位模型经过差分处理可以完全消除卫星钟差和接收机钟差的影响.而与距离相关的误差,如大气折射误差、卫星轨道误差,通过双差方法处理后,其影响也可忽略不计.但是,还有一些如多路径效应、接收机观测噪声等难以模型化的误差无法通过差分法消除,而这些难以模型化的误差会大大降低基线解算的可靠性,并影响定位精度.由于这些误差是包含在相位双差观测值中的,需采用一定的方法对相位双差观测值进行消噪以将其削弱.国内外许多学者对此进行了研究,常用的处理方法有Kalman滤波法、小波分析法等[1-2],其中尤以小波分析法应用最为广泛,并取得了良好的效果[3-5].但是利用小波分析法对相位双差观测值进行消噪时,需预先指定该小波基函数和分解尺度.这些设置常需依靠经验来确定,而小波基函数和分解尺度的不同选择会对消噪的效果产生较大的影响.

鉴于此,本文引入一种可根据数据本身特征进行自适应滤波消噪的方法——经验模式分解法,对观测值进行消噪,再用消噪后的双差观测值进行基线解算.算例分析结果表明:该方法可以明显地改善整周模糊度解算的可靠性,并提高基线解算的精度,为实现高精度的基线解算提供了新的途径.

1 单频GPS相对定位模型

设某历元2台单频GPS接收机可共视k+1颗卫星,则可组成k个载波相位双差观测方程,其线性化后的双差观测方程[6]为

式中:i——历元号;Ai——k×3系数矩阵;B1——k×k双差整周模糊度系数矩阵;Xi——基线向量改正数,X i=(δ x,δ y,δ z)T;N——k维双差整周模糊向量;L i——k维单频双差观测值向量,是观测值与计算值的差值——k维噪声向量.

设这2台GPS接收机连续观测n个历元且共视k+1颗卫星,则这n个历元总的双差观测方程为

即可表示为:L=AX+BN+ε.根据以下最小二乘准则

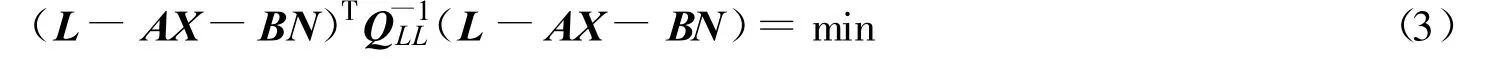
可获取模糊度的浮点解 ^N及其相应的协方差阵QNN,建立模糊度参数的搜索准则:

目前,对于式(4)所示准则进行搜索的主要方法有:序贯最小二乘平差法[7]、优化Cholesky分解法[8]、快速模糊度搜索法(FARA)[9]、LAMBDA法[10-11]等.本文将应用效率较高的LAMBDA法对模糊度进行搜索.一旦整周模糊度固定,便可以得到相应的基线向量解.

2 经验模式分解的基本原理

2.1 经验模式分解

Huang于1998年提出了一种新的处理非线性、非平稳信号的方法——经验模式分解法(empirical mode decomposition,EMD)[12].该方法吸取了小波变换多分辨率分析的优点,并克服了小波变换中需要选取小波基函数的困难,可自适应地把复杂的信号分解为若干个固有模式函数(intrinsic mode function,IMF)之和.IMF需满足以下2个条件:(a)在整个数据序列中,极值点的数目与零点的数目相等或最多相差1;(b)信号关于时间轴局部平均对称.

但在实际操作中,由于信号通常都是非线性、非稳态的,它们不满足构成IMF的条件.为此,需采用一种所谓“筛选”算法,将复杂信号进行分解.其基本步骤如下:(a)确定出信号xt的所有局部极值点,然后将所有的局部极大值点和极小值点用三次样条曲线进行连接,形成上下包络线 umax和umin;(b)根据极大值包络线与极小值包络线求取均值包络线mt=(umax+umin)/2;(c)计算xt与mt的差值dt=xt-mt;(d)重复(a)～(d)步骤,直到 dt为零均值,此时得到的 dt即为第1个IMF,记 I1=dt;(e)计算残差 rn=xt-I1并将其当作原始数据序列.对其反复计算得到n个IMF.当rn变成单调函数已不能再从中提取满足IMF的分量时,分解过程终止.原始数据序列可被表示为所有IMF与最终残差函数之和:

2.2 EMD消噪方法

使用EMD进行信号消噪时,定义如下按尺度标准化模量的累积均值[11]:

式中,mean(·)和std(·)分别为求均值和标准差函数,Ii表示第i尺度的模量,如果^hm明显偏离零值,则从尺度m开始认为是系统的趋势变化所致.消噪后的信号由下式表示:

3 基于EMD方法的单频GPS基线精化解算流程

基于EMD方法的单频GPS基线精化解算流程如下:(a)从观测文件中读取观测数据,组成双差观测方程;(b)对双差观测值进行周跳探测和修复,并剔除粗差;(c)对L1波段双差观测值采用EMD方法进行消噪.需要说明的是,由于每个卫星观测值的观测噪声不同,消噪时其尺度m可能会有所差异;(d)利用消噪后的载波相位双差观测量进行最小二乘参数估计,得到模糊度浮点解及其对应的协方差阵;(e)应用LAMBDA方法进行模糊度搜索,并采用Ratio值进行有效性检验.认为Ratio值大于2时,可以接受为模糊度整数解.在此基础上进行基线解算获得其固定解.

4 算例分析

采用2台Trimble R3单频接收机在一条短基线上采集的观测数据进行研究,数据采样频率为1s,共观测1h,截取其中的1000个历元进行分析.在分析时段中共视5颗卫星,分别为PRN2,PRN4,PRN5,PRN13,PRN17,其高度角分别为 41.15°,60.98°,15.30°,23.27°,58.07°.选择PRN4作为参考卫星,以L1波段形成 4组双差观测值PRN4-2,PRN4-5,PRN4-13,PRN4-17.数据处理时采用如下3种方案进行:方案Ⅰ取前500历元的数据求解;方案Ⅱ取后500历元的数据求解;方案Ⅲ取全部1000历元的数据进行计算.以方案Ⅲ的PRN4-2双差观测值为例,对其应用EMD进行分解,可得到4个固有模式量与1个趋势项,单位为周,如图1所示.

将图1中的高频IMFs和低频趋势项进行分离,由其标准化模量的累积均值与尺度的关系可得其在 m=4时偏离零值,应用式(6)对观测值进行消噪,其消噪前后的结果如图2所示.

对比图2(a)和(b)可以看出,使用EMD方法能有效地消除双差观测值中存在的高频噪声.对3种方案消噪前后的数据进行基线处理,并应用LAMBDA方法进行模糊度搜索,其Ratio值的比较结果为:方案Ⅰ,消噪前6.14,消噪后8.29,方案Ⅱ,消噪前13.54,消噪后23.47;方案Ⅲ,消噪前21.98,消噪后35.16。由此可以看出,利用消噪前后的数据进行计算都可以得到正确的模糊度固定解,但数据经过消噪后,其Ratio值显著增大,表明模糊度解算的可靠性大大增强.另外,方案Ⅲ的Ratio值相对于其他2种方案要大,这是由于其观测时间最长的缘故.

图1 PRN4-2双差观测值的EMD多尺度分解Fig.1 Multi-scale EMD decomposition of PRN4-2 double difference observation data

图2 PRN4-2双差观测值的消噪结果Fig.2 Denoising resu lts of PRN4-2 doub le difference observation data

将固定的模糊度代入式(1),可以计算出各组双差观测值的残差.限于篇幅,本文仅给出了方案Ⅲ各个卫星对观测值消噪前后处理结果的残差序列,如图3和图4所示.对比图3和图4可以发现,在双差观测值消噪之前,残差序列受到高频噪声的影响比较严重,双差观测值去噪后,残差序列曲线变得非常平滑,说明高频观测噪声得到较好的消除.

图3 原始双差观测值残差序列Fig.3 Residual series of original double difference observation data

图4 消噪后双差观测值残差序列Fig.4 Residual series of denoised double difference observation data

以TGO1.62商业软件解算出的坐标结果为真值,将消噪前后3种方案下的每个历元解算结果与之进行对比,进而计算出流动站的定位精度,以中误差来进行评定,其结果见表1.

从表1可以看出,在3种方案下其消噪后的x,y,z方向的中误差明显比消噪前要低,表明通过对双差观测值消噪有效提高了最终的定位精度.

表1 3种方案流动站定位精度比较Table 1 Comparison of positioning precisions of moving station between three schemes

5 结 论

a.经验模式分解方法具有根据信号本身特征进行自适应滤波消噪的功能,与小波分析方法相比,它不需要预先根据经验指定小波基函数和分解尺度,具有通用性的特点.

b.应用经验模式分解方法对双差观测值进行消噪,并在此基础上以LAMBDA方法进行整周模糊度搜索,其可靠性得到了较大的提高,同时定位精度也得到了明显地改善,达到了精化解算的目的.

c.中长基线情况下,电离层延迟、对流层延迟等误差经过双差处理后其影响难以消除且不能忽略,此时的精化解算方法还需进一步深入研究.

[1]SATIRAPOD C,RIZOS C.Multipath mitigation by wavelet analysis for GPS base station applications[J].Survey Review,2005,295(38):2-10.

[2]HAN S,RIZOS C.GPS network design and error m itigation for real-time continuous array monitoring system[C]//Proceedings of ION GPS-96,Kansas City:[s.n.],1996:1827-1836.

[3]卓宁.小波分析技术在GPS数据预处理中的应用[J].中国惯性技术学报,2009,17(2):184-186.(ZHUO Ning.Application of wavelet analysis inGPS data prep rocessing[J].Journal of Chinese Inertial Technology,2009,17(2):184-186.(in Chinese))

[4]SATIRAPOD C,OGAJA C,WANG J.An approach to GPS analysis incorporating wavelet decomposition[J].Artificial Satellites,2001,36(2):27-35.

[5]朱习军.基于小波分析的高精度GPS测量质量控制研究[D].青岛:山东科技大学,2006.

[6]OU J K,WANG Z J.An improved regularization method to resolve integer ambiguity in rapid positioning using single frequency GPS receivers[J].Chinese Science Bu lletin,2004,49(2):196-200.

[7]EULERH J,LANDAU H.Fast GPS ambiguity resolutionon-the-fly for real-time application[C]//Proceedingsof the Geodetic Symposium on Satellite Positioning,Ohio City:[s.n.],1992:650-659.

[8]HATCH R,EULER H J.Comparison of several AROF kinematic techniques[C]//Proceedings of ION GPS-94,Salt Lake City:[s.n.],1994:363-370.

[9]CHEN D.Development of a fast ambiguity search filtering(FASF)method for GPS carrier phase ambiguity resolution[D].Calgary,Canada:University of Calgary,1994.

[10]TEUNISSEN P J G.The Least-squares ambiguity decorrelation ad justment:a method for GPS integer ambiguity estimation[J].Journal of Geodesy,1995,70(1/2):65-82.

[11]黄张裕,刘胜男,陈苏娟.一种改进的GPS模糊度空间搜索算法[J].河海大学学报:自然科学版,2011,39(1):89-94.(HUANG Zhang-yu,LIU Sheng-nan,CHEN Su-juan.Modified space searching algorithm for GPS ambiguity[J].Journal of Hohai University:Natural Sciences,2011,39(1):89-94.(in Chinese))

[12]HUANG N E,SHEN Z,LONG S R.The empirica lmode decomposition and hilbert spectrum for nonlinear and non 2 stationary time series analysis[J].Proceedings of the Royal Society of London SERIESA,1998,454:903-995.