计算机CPU热管散热器换热性能研究

王 鹏,叶 立,许 伍,胡永海

(上海理工大学能源与动力工程学院,上海,200093)

近年来,随着电子工业的迅猛发展,各种电子设备也越来越向高频、高集成化发展,从而导致其发热量逐年增加。同时,由于使用了以集成电路和大规模集成电路的小型化部件,趋向于高密度装配,因而单位容积的发热量逐年增大。一个最典型的例子就是电子计算机芯片近年来的发展。为了保证电脑CPU正常运行,需要使内装电子元件维持在一定温度范围内运转[1]。这是因为电子元件的性能对温度非常敏感,温度过高或过低,元件性能将显著下降,不能稳定工作,从而也将影响到整个系统的可靠运行。当今电子产品的热设计中,由于热流量的不断提高,仅采用标准的翅片式散热片很难满足要求。热管由于其导热性能好,热阻小,可将热量稳定地由一处传递到另一处,故通过热管将热量由小空间处传递到一定距离外的相对大空间里的散热片上,可利用空气自然对流的方式达到电子产品换热的目的[2～5]。

基于上述分析,本文分别建立了热管式散热器与普通翅片散热器几何模型,利用ANSYS软件进行热特性比较分析,模拟计算出稳态温度场分布,以及不同功率下CPU中心点的传热特性,并对计算结果进行了实验验证。

1 数值模型

1.1 模型建立及网格划分

本文所研究的流体在管间及管束周围的流动与换热情况是一种典型的多尺度、大分离复杂流场计算。为获得较高精度,计算所需用网格数相当庞大,使得计算趋于困难。考虑到本文所提出的模型本质上为周期性结构,此处将其简化为单流道进行处理,其三维模型如图1所示。各几何结构参数为:热源CPU长20mm,宽20mm,高h=1.75mm,CPU安装铜片厚度5mm,热管和翅片高度均为80mm,其间隔均为8mm,热管直径与铜管直径均为5mm。通过空气自然对流进行换热,周围空气处于室温20℃,空气对流换热系数12W/m2℃。

控制方程为二维不可压缩流雷诺时均N-S方程。雷诺应力采用k-ε湍流模型进行估计。

图1 热管式与普通铜管散热器单流道模型

计算采用基于有限体积法的Simple系列方法,其中能量方程、动量方程、湍动能、湍流耗散率均采用具有三阶精度的Quick格式离散。计算首先选用较小的欠松弛因子和一阶迎风格式得到初值,然后采用二阶迎风格式得到最终结果。

为了准确地模拟出管壁附近流动和换热以及管内的导热,同时又要控制网格的数目,划分网格时,采用非均匀网格,对压力、速度和温度梯度比较大的管壁及导流翼附近区域网格进行局部加密处理以提高这些区域内解的分辨率。管路区域网格采用六面体,其他区域采用四面体,整个计算域网格数量近80万,网格质量Skewness值小于0.8。

计算域左界面设定为入口速度边界条件,计算域右界面设定为压力出口边界条件,CPU设为发热源,发热量给定常数作为热边界条件,计算域下界面设为轴对称边界。各计算参数下降三个数量级并达稳定,进出口质量流量相差0.1%以下作为残差收敛标准。

1.2 假设条件及材料物性参数

进行计算时对所建立的数值模型作如下假设:

(1)热管的材料性质不随时间的改变而改变。

(2)热管为一实心固体,以此计算热管等效传热系数。

(3)CPU在连续工作一段时间后,达到热平衡状态,可以看做稳态热传导问题。

(4)忽略辐射换热。

CPU的材料属于典型复合材料,其力学参数和热学参数都比较难以确定。为了简化计算,本文把CPU看成均质各向同性材料,即用晶体管的性质作为整个CPU模型的热学参数,计算所需材料物性参数如表1所示。

表1 材料物性参数

2 模拟结果及分析

2.1 热管式散热器与普通翅片散热器稳态工作情况下的温度分布

图2 翅片散热器工作1800秒时温度分布图

图3 热管散热器工作1800秒时温度分布图

普通翅片散热器和热管式散热器的稳态温度分布图如图2和图3所示,此时CPU功率为40W,散热器工作1800秒。从图中可看出普通翅片散热器中存在较明显的温度分布,从翅片根部 (热源端)向翅片自由端部递减,温度梯度跨度较大;而热管式散热器中温度分布比较均匀,温度梯度很小,说明热管式散热器比普通翅片散热器拥有更好的均温性。两种散热器中温度最大值均出现在CPU发热块中心处,普通翅片散热器的最高温度值为379.6K,热管式散热器的最高温度值为351.4K,二者相差28.5℃,说明热管式散热器比普通翅片散热器拥有更好的热传导性能。

2.2 不同功率下热管式散热器和普通翅片散热器中心点温度随时间的变化关系

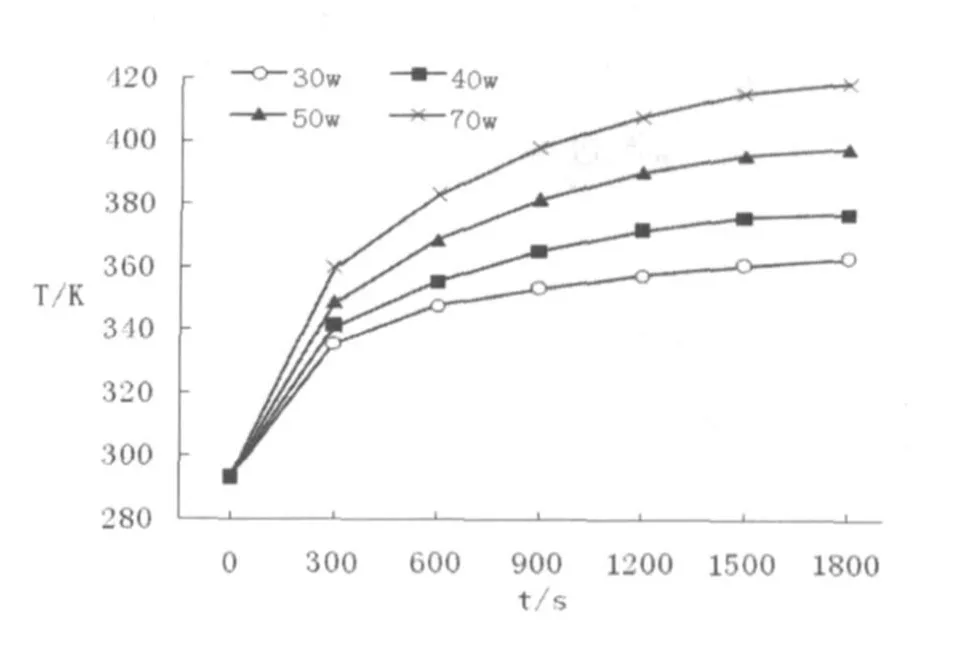
图4 普通翅片散热器在不同CPU功率下的温度-时间曲线图

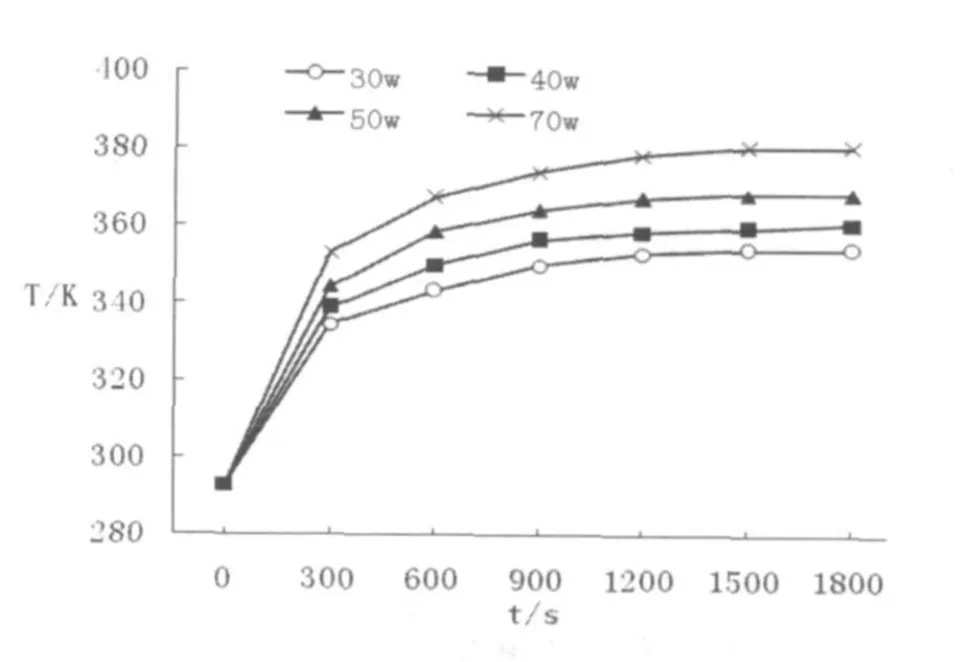
图5 热管式散热器在不同CPU功率下的温度-时间曲线图

随着集成化趋势的形成及电脑配置的不断提高,CPU功率也在不断增加。文中对不同功率下普通翅片散热器和热管式散热器中心点温度随时间的变化关系进行了计算,并对二者在高CPU功率下的散热特性进行了比较,计算结果如图4、图5所示。两种换热器中心点温度随时间的变化关系非常相似,在初始阶段都上升较快,随时间进行上升趋势逐渐趋缓,于1800秒左右都基本达到稳定,但二者的具体温度值有所不同。当CPU功率较小时(例如P=30W),热管式散热器和铜管散热器中心点的最高温度值都小于363K,在CPU所能承受的正常范围内。当CPU功率上升至50W时,普通翅片散热器中心点最高温度值已达到375K以上,超出了CPU所能承受的范围,无法满足换热要求;而此时热管式散热器中心点最高温度值仍保持在360K左右,可保证CPU的正常运行。在CPU高功率运行工况下,使用热管式散热器比使用普通翅片散热器更具有优势,即使CPU功率升至70W及更高值时,也可以通过添加热管数量的方式轻松实现CPU温度控制。

3 模拟结果的实验验证

3.1 实验装置

CPU热管式散热器实验系统如图6所示,整个系统由风机、数据采集器、加热器以及热管散热器四部分构成。为使空气流经热管换热器后速度分布接近均匀,采用了较长的入口段。热管加热方式采用电加热,电加热热源由模拟加热块通过五根电阻丝加热棒提供,加热功率大小由变压器控制,显示于电流电压表上。热管表面温度由三个热电偶测定,热电偶测点R1、R2和R3位置如图7所示,各测点温度值均由数据采集仪 (HP34970A)记录。

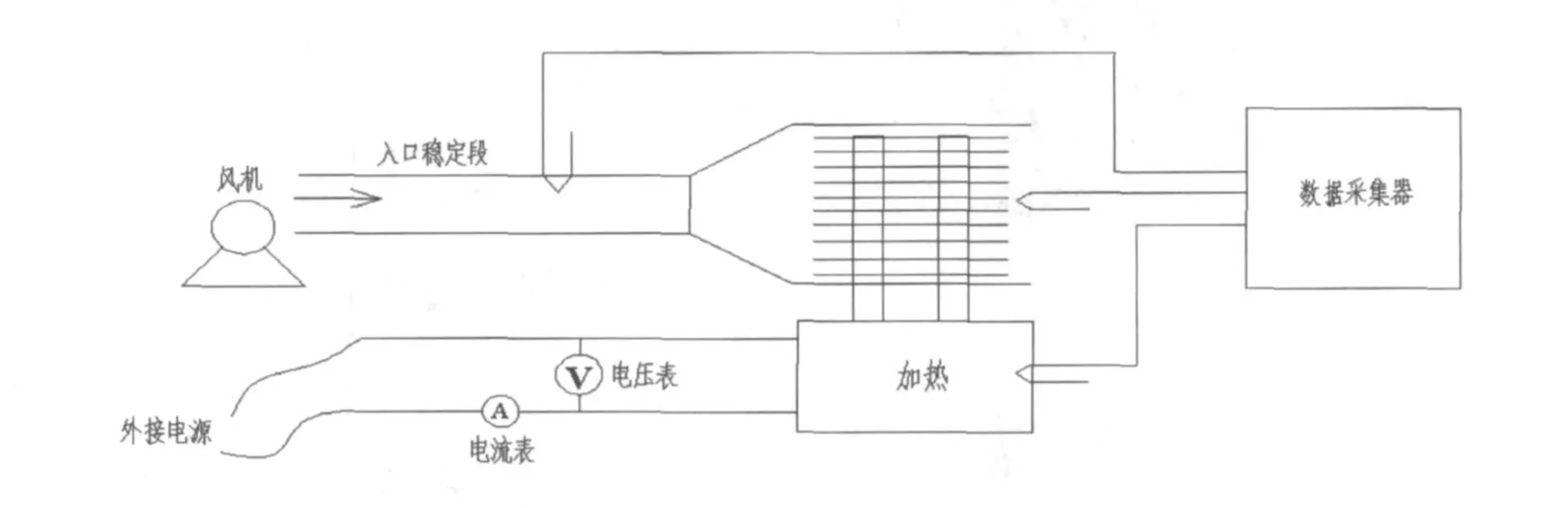
图6 CPU热管式散热器实验装置图

图7 实验测点位置图

3.2 实验值与计算值的比较

CPU功率为40W,空气流态为自然对流,空气流速取0.2m/s、0.4m/s、0.6m/s三组,环境温度20℃。散热器工作1800秒后认为其进入稳定工作状态,开始测取表面温度。

图8列出了热管式散热器在不同空气流速下三测点所测得温度值和相应位置处的模拟计算温度值。实验结果表明,当空气流速为0.4m/s时,模拟计算值与实验值吻合最好;此时的三测点中,R1处的实验测得值与计算值相差最大,约4.5℃,据推测可能是由于CPU与热管接触处存在导热硅胶热阻所致。

测点实验值与计算值基本吻合,证明了所用数值模型的正确性和计算结果的可信性。

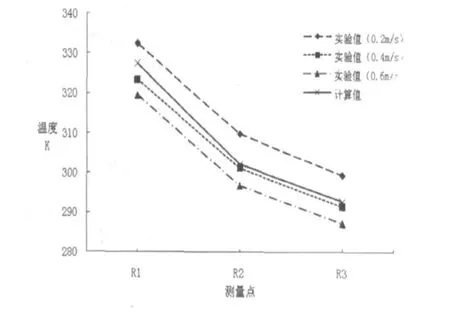
图8 热管式散热器测点实验值与计算模拟值对比

4 结语

计算机的高度集成化发展,导致了计算机芯片单位容积放热量的逐渐增大,为满足CPU正常运行时对最高温度和表面温度均温性的限制要求,本课题对CPU热管式散热器和普通翅片散热器进行了数值模拟,对两种散热器在稳态工作情况下的温度分布规律及不同功率下散热器中心点温度随时间的变化关系进行了比较,并搭建实验台对热管式散热器进行了温度测定。通过计算和实验可得到以下结论:

(1)稳态工作情况下,热管式散热器表面温度分布均匀,具有很高的等温特性;而普通翅片散热器则存在明显的温度梯度跨度。

(2)热管式散热器的热传导性能远高于普通翅片散热器,相同情况下 (CPU功率=40W),热管式散热器CPU发热块中心处的最高温度值比普通翅片散热器CPU发热块中心处的最高温度值低28.5℃。

(3)热管式散热器比普通翅片散热器更能满足CPU高功率运行的散热要求,并可通过添加热管数量的方式轻松实现对散热效果的控制。

(4)实验测得数据和计算模拟数据基本吻合,证明了计算模型的正确性和计算结果的可信性。

本研究对于计算机CPU散热器传热性能分析及其优化设计具有一定指导意义。

[1] 张德君,杨志刚,孙晓峰.计算机芯片冷却技术的现状与发展[J].机械设计与制造,2008(3):12-13

[2] 李炎炎,张永恒.CPU散热器换热特性的数值研究[J].制冷与空调,2007,21(4):98-100

[3] Leonard L.Vasiliev.Heat pipes in modern heat exchangers

[J] Applied Thermal Engineering,2005(25):18-20

[4] 陶汉中,张红,庄骏.高速芯片模块热管散热器的数值传热分析[J].南京工业大学学报,2004,26(1):68-71

[5] Pastukhov V.G.,Maidanik Yu F.,Vershinin C.V.Miniature loop heat pipes for electronics cooling[J].Applied Thermal Engineering.2003,23(9):1125-1135