湍流涡黏性模型方程中相位差的测量

郭爱东，姜 楠，贾永霞

（1.天津大学力学系，天津 300072；2.天津市现代工程力学重点实验室，天津 300072；3.军事交通学院装运机械系，天津 300161）

湍流涡黏性模型方程中相位差的测量

郭爱东1，3，姜 楠1，2，贾永霞1

（1.天津大学力学系，天津 300072；2.天津市现代工程力学重点实验室，天津 300072；3.军事交通学院装运机械系，天津 300161）

基于理论上湍流相干结构复涡黏性模型对涡黏性系数的分析，应用热线测速技术测量了平板湍流边界层多尺度相干结构动力学方程中非相干结构成分对相干结构贡献的雷诺应力分量与相干结构流向速度流向变形率之间的相位差。分析了湍流边界层相干结构猝发过程中，非相干结构成分对相干结构贡献的雷诺应力分量与相干结构流向速度流向变形率之间的相位差沿湍流边界层法向的变化规律，为建立更加符合实际的湍流模型提供了实验依据。

湍流边界层；多尺度相干结构；涡黏性模型；雷诺应力；速度变形率；相位差

0 引 言

1895年，雷诺提出统计平均的方法，将不规则的湍流运动分解为系综平均量和脉动量两部分，把它代入Navier－Stokes方程后得到控制平均流动的雷诺平均方程，雷诺平均方程与Navier－Stokes方程最大的区别是含有脉动速度的二阶关联项——雷诺应力项，使得描述湍流平均运动的雷诺平均方程不封闭。为了解决雷诺平均方程的不封闭性问题，依靠理论与经验的结合，对雷诺应力项引进一系列模型假设，使雷诺平均方程封闭，建立描写湍流平均量的封闭方程组的理论计算方法，就是所谓的湍流模式理论。涡黏性模型是湍流模式理论中应用最为广泛的一种。

从20世纪中叶开始，人们普遍认为在湍流场中，除平均流外，同时还存在着不同尺度的相干结构成分和随机脉动成分（非相干结构成分），所有与流动有关的物理量都可以分解为3部分［1］：

如果用˜f表示对f的长时间平均，〈f〉表示对f的相位平均，考虑不可压缩流体动量方程为：

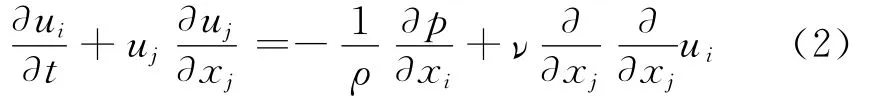
连续性方程为：

将速度场和压力场按如下方式进行三项分解：

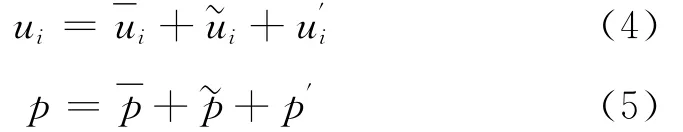
将式（4）和式（5）分别代入式（2）和式（3），将得到的式子分别做相位平均和长时间平均，并用方程的相位平均减去长时间平均，可以得到相干结构满足的方程：

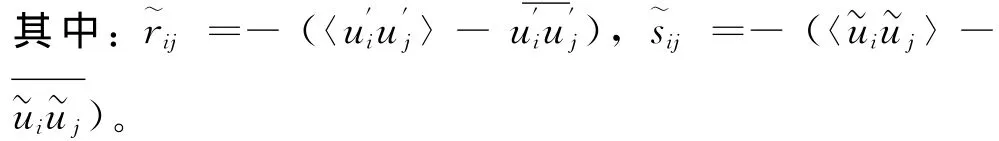
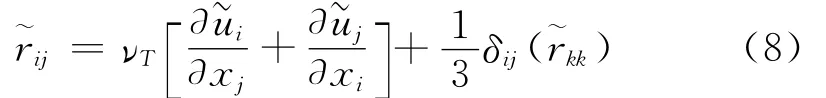
的形式，其二维模型为：

钻具组合：CK306B定向随钻扩孔钻头×0.48 m+120 mm(1.75°)单弯螺杆+(331 mm×310 mm)接头+88.9 mm无磁钻杆(1根)+120 mm MWD短节+(311×310)接头+挡板+88.9 mm无磁钻杆(1根)+88.9 mm斜坡钻杆(20根)+旁通阀+88.9 mm加重钻杆(45根)+88.9 mm斜坡钻杆+127 mm钻杆。

式中，νT为涡黏性系数，该湍流模型即为涡黏性模型。

对于湍流相干结构涡黏性模型的研究经历了一个长期的过程。从19世纪70年代起，依照流动稳定性理论，Reynolds［1］、Wu［2］、罗纪生和周恒［3］分别提出了用流动稳定性理论解释湍流边界层外区大尺度相干结构的理论模型。这些理论模型对其中涡黏性系数的形式有不同的假定，Reynolds假定的涡黏性系数是个实数，Wu假定的涡黏性系数是复的常数，Reynolds和 Wu的假定都与 Brown［4］、Falco［5］的实验不符；罗纪生和周恒［3］针对湍流边界层外区提出的是大小沿平板法向位置变化的复涡黏性系数模型，得到的结果与Antonia［6］的实验符合较好。

将涡黏性系数设成复数，相当于认为非相干结构成分对相干结构贡献的雷诺应力与相干结构的速度变形率之间存在着相位差，这种观点是比较符合实际的，有理论上的合理性，也得到了 Brown［4］、Falco［5］、Antonia［6］、Wu［2］、罗纪生和周恒［3］、王昕［7］、Wang［8］以及李万平［9］、罗纪生和王新军［10］等人在数值模拟和实验等方面的验证。

Wang［8］和罗纪生［10］等对壁面沿流向周期分布法向速度边界条件的槽道湍流进行了直接数值模拟，认为具有波数α成份的沿流向周期变化的雷诺应力复涡黏性模式应该表示为：

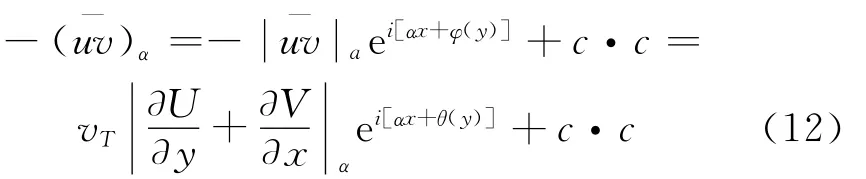
其中，c·c表示复数共轭，而涡黏性系数的表达形式为：

根据他们的分析，相位信息φ（y）、θ（y）应该是随壁面法向坐标y变化的函数。

为了建立更加符合流动实际的湍流相干结构模型，正确测量随壁面法向坐标y变化的相位信息φ（y）、θ（y），得到湍流相干结构猝发过程中随机脉动对相干结构贡献的雷诺应力与速度变形率之间的相位差显得尤为重要与关键。姜楠和郭爱东［11］应用双丝热线测速技术，对平板湍流边界层外区多尺度相干结构剪切雷诺应力分量与流向速度法向变形率之间的相位关系进行了实验测量，研究了相干结构剪切雷诺应力分量与流向速度法向变形率之间的相位差沿湍流边界层法向的变化规律，肯定了湍流相干结构复涡黏性系数模型的合理性。

1 实验设备与测量方法

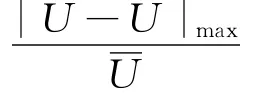
实验用1500mm×800mm光滑平板水平放置在风洞实验段内，正对来流方向的平板前缘为楔形，平板前缘固定有绊线并贴有砂纸，以加速边界层转捩，保证在探针测量位置形成充分发展的湍流。在距离平板前端800mm处，用美国TSI公司IFA300型恒温热线风速仪和TSI－1244－T1.5型双平行丝热线探针进行测量，热线探针的热线敏感材料是直径为5μm的钨丝，双平行丝热线探针由两个间距为1mm的相互平行的热线敏感元件组成，用于测量空间距离为1mm的空间两点的流向速度及沿流向的速度变形率。实验时大气压强为1.01×105Pa，风洞中气流温度为19.5°C。用 TSI－1244－T1.5型双平行丝热线探针测量湍流边界层流向速度分量及沿平板流向的变形率，测量时两根平行的热线水平放置，与自由来流方向垂直，与平板平行，一根在上游，一根在下游。测量过程中保证两根热线始终在流场的同一水平高度且沿平板法向移动。共测量106个测点，得到湍流边界层内两组不同法向位置的瞬时流向速度的时间序列信号。对测得的两组瞬时流向速度信号进行差分计算，得到湍流边界层的瞬时流向速度流向变形率的时间序列信号。实验中，湍流脉动速度信号的采样频率为50kHz，每个测点采集的数据量为1048576，采样时间为20.97s。

2 结果分析与讨论

图1 来流速度为13.1m／s时y＋＝86.8处两个通道的瞬时流向速度和流向速度的流向变形率时间序列信号Fig.1 Time sequence signals of two－channel longitudinal velocity and their strain rate at y＋ ＝86.8when U∞ ＝13.1m／s

图1分别是来流速度为13.1m／s时，在y＋＝86.8处，用 TSI－1244－T1.5型双平行丝热线探针测得的两个通道的瞬时流向速度的时间序列信号以及经计算后得到的流向速度的流向变形率的时间序列信号。为了将湍流小尺度脉动的细节尽可能地显示清楚，图中只给出了8.00～8.05s时间段内的部分。

在实验数据分析过程中，用子波变换对湍流脉动速度信号进行多尺度分解，将湍流脉动速度信号分解成20个尺度。子波尺度依据湍流脉动速度信号的采样频率和子波母函数的滤波特性自动进行频带划分，对实验采集的离散信号自动进行低通和高通共轭数字滤波。用自相关方法确定不同尺度湍涡结构的时间尺度，根据子波系数的瞬时强度因子检测平板湍流边界层多尺度相干结构，分离出湍流边界层流向速度多尺度相干结构成分及非相干结构成分［12］。以相干结构流向速度分量的相位平均波形为基准，用条件相位平均技术提取了平板湍流边界层多尺度相干结构流向速度的流向变形率和非相干结构成分对相干结构贡献的雷诺应力条件相位平均波形。

图2给出了用子波分解得到的湍流脉动动能在20个尺度中的分布，可以发现第8尺度为能量最大尺度。图3给出各尺度子波系数的平坦因子。从图3可以看出，前8个尺度的分尺度平坦因子大于3，表明在前8个尺度中存在相干结构，相位平均波形的结果也表明了这一点。前8个尺度的相干结构的相位平均波形具有很光滑的波形曲线，说明相干结构具有典型的拟序特征，其发展演化具有很强的规律性。而9尺度以后的分尺度平坦因子小于3，其相位平均波形曲线很不光滑，没有规律性，属于完全随机的脉动。

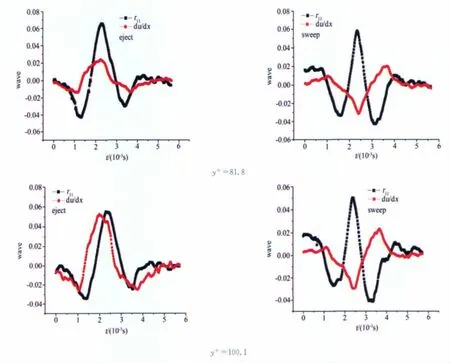
根据文献［13］的分析，在本文实验条件下，时间耗散尺度大约为1～2个粘性时间单位，相当于时间尺度不超过0.0005s，所以前8个尺度中，第1、2、3尺度为耗散尺度。而第4、5、6尺度的能谱符合Kolmogorov－5／3标度律［14］，为惯性子区尺度，第7、8尺度为大尺度的含能区尺度［15］。给出了第2、5、7三个尺度的条件相位平均波形的图形，它们分别代表了耗散尺度、惯性子区尺度、含能区尺度的相干结构的典型特征。图4、5、6分别是第2、5、7尺度，法向坐标y＋分别为81.8、100.1、287.9时，与相干结构喷射和扫掠过程相对应的非相干结构成分对相干结构贡献的雷诺应力分量的条件相位平均波形与流向速度流向变形率条件相位平均波形的比较，从图中可以看出，与相干结构喷射和扫掠过程相对应的非相干结构成分对相干结构贡献的雷诺应力分量与流向速度流向变形率之间存在着相位差ΔΦ＝φ（y）－θ（y）。

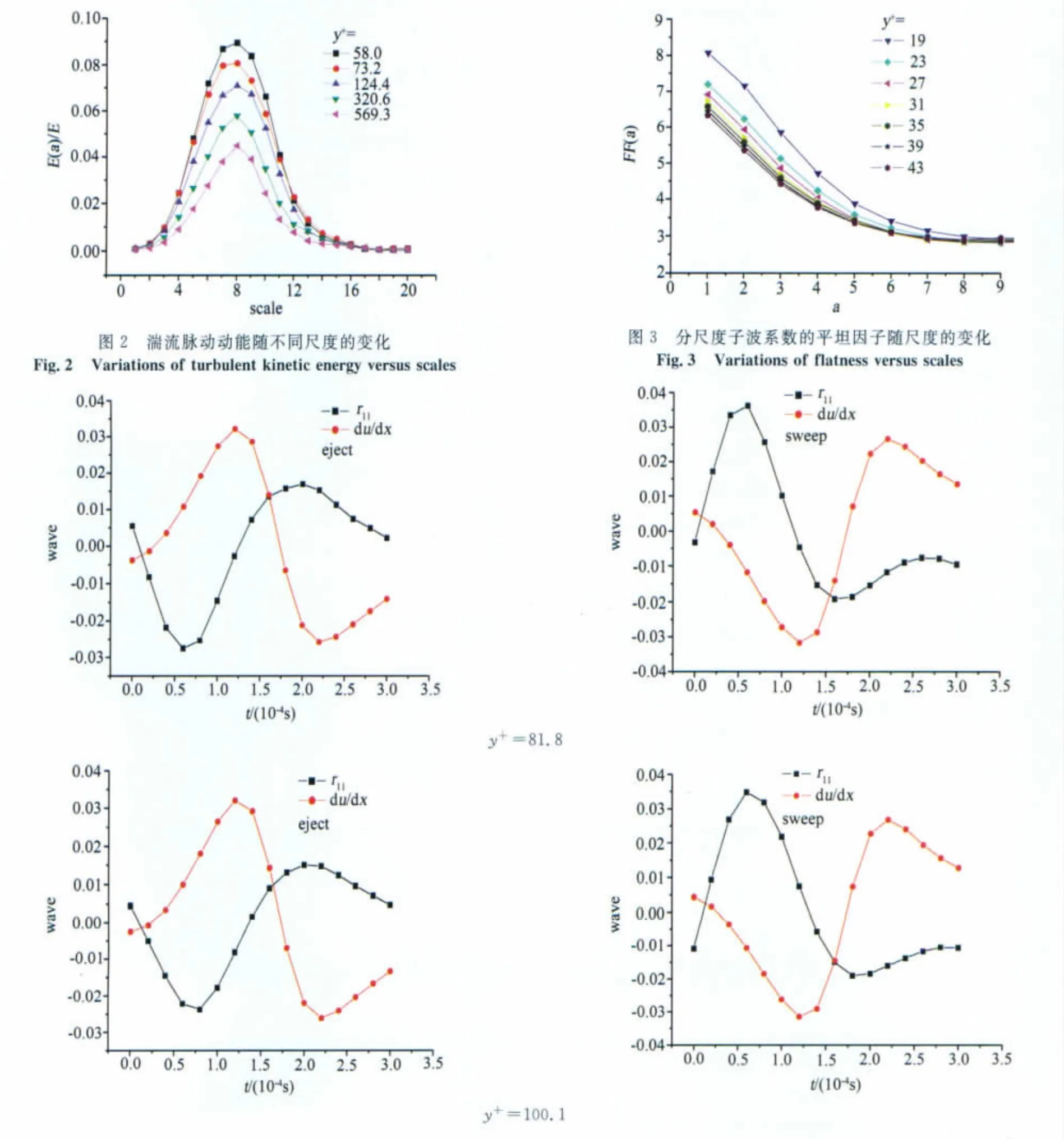
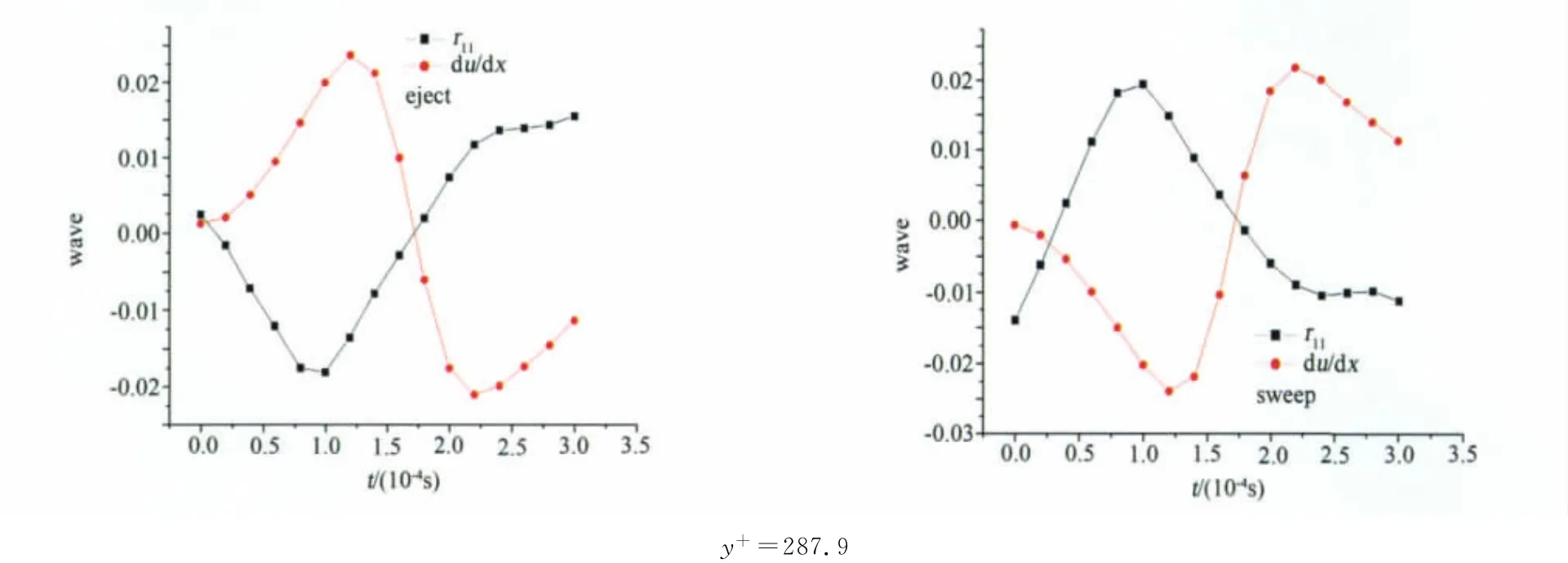
图4 第2尺度y＋分别为81.8、100.1、287.9时喷射和扫掠过程中非相干结构成分对相干结构贡献的雷诺应力与相干结构流向速度流向变形率的条件相位平均波形比较Fig.4 Comparison of conditional phase average waveforms between Reynolds stress that noncoherent structures component contribute to coherent structures and longitudinal strain rate of longitudinal velocity of coherent structures in ejecting and sweeping process at y＋ ＝81.8，100.1and 287.9for scale＝2

用互相关技术计算非相干结构成分对相干结构贡献的雷诺应力条件相位平均波形与流向速度流向变形率条件相位平均波形对应不同相位差的互相关系数，确定互相关系数取得最大值时的相位差即为非相干结构成分对相干结构贡献的雷诺应力与流向速度流向变形率之间的相位差，经计算得到平板湍流边界层不同法向位置的相位差，进而研究相位差沿平板湍流边界层法向的变化规律。图7显示的是不同尺度的相干结构喷射和扫掠时非相干结构成分对相干结构贡献的雷诺应力与相干结构流向速度流向变形率之间的相位差沿平板湍流边界层法向的变化规律。可以看出，在湍流边界层中，非相干结构成分对相干结构贡献的雷诺应力分量与相干结构的流向速度流向变形率之间的相位差不仅与相干结构的尺度有关，还与相干结构喷射和扫掠的具体物理过程有关：喷射阶段非相干结构成分对相干结构贡献的雷诺应力相位滞后于相干结构流向速度流向变形率相位，相位差基本不随尺度变化，相位差在对数律层以内在－120°～－160°之间基本不随壁面法向变化，在外区随壁面法向逐渐增加至0°；扫掠阶段非相干结构成分对相干结构贡献的雷诺应力相位超前于相干结构流向速度流向变形率相位，小尺度相干结构扫掠的相位差略小，大尺度相干结构扫掠的相位差略大，随尺度增加相位差逐渐从150°增加到180°，相位差在对数律层以内基本不随壁面法向变化，在外区随壁面法向逐渐减小至100°。

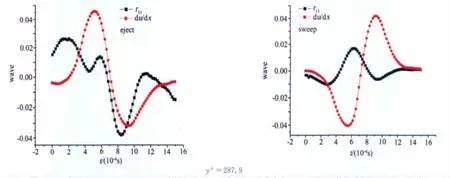
图5 第5尺度y＋分别为81.8、100.1、287.9时喷射和扫掠过程中非相干结构成分对相干结构贡献的雷诺应力与相干结构流向速度流向变形率的条件相位平均波形比较Fig.5 Comparison of conditional phase average waveforms between Reynolds stress that noncoherent structures component contribute to coherent structures and longitudinal strain rate of longitudinal velocity of coherent structures in ejecting and sweeping process at y＋ ＝81.8，100.1and 287.9for scale＝5

3 结 论

通过对平板湍流边界层不同尺度的相干结构喷射和扫掠过程中非相干结构成分对相干结构贡献的雷诺应力分量与相干结构流向速度流向变形率之间相位差的实验测量与计算分析，得到以下结论：

（1）在用湍流涡黏性模型计算雷诺应力时，应该充分考虑到宏观尺度的湍涡结构之间相互作用引起动量传递的时空弛豫效应，即湍流应力与平均速度变形率在时间和空间上的不同步性，用带时空相位变化的涡黏性系数对平均速度变形率的相位进行修正，使得雷诺应力分量和平均速度变形率相位对齐，才能得到正确的雷诺应力分布。所有在时空上存在周期变化的流动结构的湍流都存在类似的问题。以前由于实验技术的限制，这个问题并未引起足够的注意。因此，复涡黏性系数形式的湍流雷诺应力模型是合理的；

（2）具有宏观尺度的湍流相干结构间的动量传递与相干结构运动变形的弛豫时间不能忽略不计，表现为非相干结构成分对相干结构贡献的雷诺应力分量和相干结构速度变形率之间的不同步性，它们之间存在着时空上的相位差，这是目前用于非定常湍流结构的涡黏模式理论需要考虑的一个重要因素；

（3）非相干结构成分对相干结构贡献的雷诺应力分量与相干结构流向速度流向变形率之间的相位差不仅与相干结构的尺度有关，还与相干结构喷射和扫掠的具体物理过程有关，喷射阶段非相干结构成分对相干结构贡献的雷诺应力相位滞后于相干结构流向速度流向变形率相位，相位差基本不随尺度变化，相位差在对数律层以内在120°～160°之间基本不随壁面法向变化；扫掠阶段非相干结构成分对相干结构贡献的雷诺应力相位超前于相干结构流向速度流向变形率相位，小尺度相干结构扫掠的相位差略小，大尺度相干结构扫掠的相位差略大，随尺度增加相位差逐渐从150°增加到180°，相位差在对数律层以内基本不随壁面法向变化。

［1］KLINE S J，REYNOLDS W C，SCHRAUB F H，et al.The structure of turbulent boundary layer ［J］.J Fluid Mech.，1967，30：741－774.

［2］WU X S，ZHOU H.Linear instability of turbulent boundary layer as a mechanism for the generation of large scale coherent structures［J］.Chinese Science Bulletin，1989，34（20）：1685－1690

［3］罗纪生，周恒.湍流边界层外区大尺度相干结构的理论模型及与实验的比较［J］.中国科学（A 辑），1993，23（1）：56－62.

［4］BROWN G L，THOMAS A S W.Large structure in a turbulent boundary layer［J］.The Physics of Fluids，1977，20（10）：S243－S252

［5］FALCO R E.Coherent motions in the outer region of turbulent boundary layers［J］.The Physics of Fluids，1977，20（10）：S124－S132.

［6］ANTONIA R A，BISSET D K，BROWNE L W.Effect of Reynolds number on the topology of the organized motion in a turbulent boundary layer［J］.J.Fluid Mech，1990，213：267－286.

［7］王昕，连源.湍流边界层复涡黏模式的实验研究［J］.力学学报，2002，34（3）：519－524.

［8］WANG X J，LUO J S，ZHOU H.On the eddy viscosity model of periodic turbulent shear flows［J］.Acta Mechanica Sinica，2003，19（5）：470－475.

［9］李万平，王小庆，谢华.湍流边界层雷诺应力和壁脉动压强相位滞后分析［J］.华中科技大学学报（自然科学版），2007，35（4）：122－125.

［10］罗纪生，王新军.壁面定常波纹状吹吸槽道流中湍流特性的研究［J］.力学学报，2005，37（6）：673－681.

［11］郭爱东，姜楠.壁湍流多尺度相干结构复涡黏模型的实验研究［J］.力学学报，2010，42（2）：159－168.

［12］JIANG N，LIU W，LIU J H，et al.Phase－averaged waveforms of Reynolds stress in wall turbulence during the burst events of coherent structures［J］.Science in China（Series G），2008，51（7）：857－866.

［13］姜楠，王瑞新.湍流边界层中微小尺度流动结构的精细实验测量［J］，哈尔滨工程大学学报，2006，27（5）：644－648.

［14］JIANG Nan，ZHANG Jin.Detecting multi－scale coherent eddy structures and intermittency in turbulent boundary layer by wavelet analysis［J］.Chinese Physics Letter，2005，22（8）：1968－1971.

［15］姜楠，王振东，舒玮.辨识子波分析壁湍流猝发事件的能量最大准则［J］.力学学报，1997，29（4）：406－411.

郭爱东（1972－），男，辽宁沈阳人，天津大学力学系博士研究生。研究方向：湍流与实验流体力学。通讯地址：天津大学力学系流体力学实验室（300072），联系电话：022－27403574，E－mail：jjxyguoj＠sina.com。

Measurement of phase difference for eddy viscosity model equation of turbulence

GUO Ai－dong1，3，JIANG Nan1，2，JIA Yong－xia1
（1.Dept.of Mechanics of Tianjin University，Tianjin 300072，China；2.Tianjin Key Laboratory of Modern Engineering Mechanics，Tianjin 300072，China；3.Handling Equipment Mechanical Department，Academy of Military Transportation，Tianjin 300161，China）

Based on the analysis of eddy viscosity coefficient of turbulent coherent structures complex eddy viscosity model in theory，the measurement technique of constant temperature anemometry has been used to measure the phase difference between Reynolds stress component that noncoherent structures component contribute to coherent structures and longitudinal velocity strain rate of longitudinal velocity of coherent structures in the dynamic model equation of multiscale coherent structures in turbulent boundary layer over smooth surface.The variational law of phase difference in the course of coherent structures bursting along normal direction in turbulent boundary layer has been analysed，which offers experimental evidences for constituting more actual turbulent model.

turbulent boundary layer；multi－scale coherent structures；eddy viscosity model；Reynolds stress；velocity strain rate；phase difference

O357.5

A

1672－9897（2011）04－0001－08

2010－10－26；

2011－11－23

国家自然科学基金重点项目（10832001），面上项目（10872145），中国科学院力学研究所非线性力学国家重点实验室对外开放课题，天津大学科技创新基金