单一来源再生混凝土抗压强度分布曲线分析

杜云晶 张灵坤

抗压强度是再生混凝土的基本力学性能，国内外对再生混凝土力学性能的试验主要考虑不同取代率对再生混凝土抗压强度的影响。极少数学者对再生混凝土抗压强度分布曲线进行了试验研究，对其进行模拟分析的更屈指可数，缺乏理论支持。因此，对单一来源再生混凝土的抗压强度分布曲线进行模拟具有重要意义。

1 蒙特卡罗方法

蒙特卡罗法又称随机抽样技巧、概率模拟方法和统计实验法［1］，它是将不确定因素引入结构计算中的数值分析方法的一种，是目前结构可靠度计算中被认为相对精确的一种方法。其理论基础是概率论中的大数定理，设x1，x2，…，xn是n个独立的随机变量，若它们来自同一母体，有相同的分布，且具有相同的有限均值和方差，分别用 μ和 σ2表示，则对于任意的 ε＞0有:

另有，若随机事件A发生的概率为P(A)，在n次独立实验中，事件A发生的频数为m，频率为W(A)=m/n，则对于任意的

1.1 再生混凝土抗压强度的随机理论计算模型

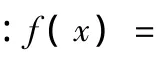
由此，将各组再生混凝土抗压强度的统计参数，即μ和σ代入F(x)，根据每一次模拟过程中不同的随机数αi，可求出对应的抗压强度值mi，从而实现了再生混凝土抗压强度的蒙特卡罗随机模拟过程。

1.2 生成MATLAB计算程序

通过上述结论得出的再生混凝土抗压强度的随机理论计算模型，为了检验统计所得的分布函数是否合理，我们利用数学分析软件MATLAB进行编程和计算。

建立MATLAB文件zubie.m，程序的变量定义中，μ的值表示为数组mm，σ表示为数组dd，随机数αi表示为数组A，与αi对应的抗压强度值mi表示为数M。各组正态分布统计参数μ和σ作为原始数据保存在EXCEL文件input.xls中。zubie.m程序读取input.xls文件中的原始数据，经过随机模拟和计算，得到随机数αi和对应的抗压强度值 mi，并存入 output.xls中。

我们根据计算模型写出zubie.m程序如下:

function fun=zubie()

filename='input.xls';

num=xlsread(filename);

num=num';

n=size(num，1);

for i=1:n

c=0;

mm=num(i，1) % μ

dd=num(i，2) % σ

t=sym('t'); %定义变量

A=0;

B=0;

rand('state'，sum(100*clock)); %保证每次的随机数不一样

A=rand(1，1000); %生成随机数为1000个

A=(round(A.*100))./100;

% f=(1/(sqrt(2*pi)))*exp(－t^2/2) 标准正态分布的密度函数

% int(f，－inf，t) 标准正态分布密度函数的原函数

% ans=

% 7186705221432913/36028797018963968*2^(1/2)*pi^(1/2)+7186705221432913/36028797018963968*pi^(1/2)*2^(1/2)*erf(1/2*2^(1/2)*t)

% solve函数中的那个函数即本文中所求函数;

% a=［0，0.5，0.5398，0.5793，0.6179，0.6654，0.6915，0.7257，0.7580，0.7881，0.8159，0.8413］;

for j=1:1000

B(j)=solve(［'7186705221432913/36028797018963968*2^(1/2)*pi^(1/2)+7186705221432913/36028797018963968*pi^(1/2)*2^(1/2)*erf(1/2*2^(1/2)*t)='，num2str(A(j))］);

end

for j=1:1000

C(j)=B(j)*dd+mm;

end

C=(round(C.*100))./100;

%求解结束，求出来是标准正态分布下的值，以下是恢复标准正态分布并存储

M=reshape(C，100，10)

filename1=［'output'，num2str(i+1)，'.xls'］;

A=reshape(A，100，10);

xlswrite(filename1，A，'Sheet1'，'A1');

xlswrite(filename1，M，'Sheet2'，'A1');

fun=M;

2 蒙特卡罗随机模拟试验计算结果

借鉴肖祥、袁飚、叶孝恒等人的试验数据，通过运行zubie程序，根据各组再生混凝土抗压强度不同的μ和σ值，我们对F(x)进行多次求解，得出各组不同强度等级下样本大小为1000的随机数αi和抗压强度值mi，计算结果如表1所示。限于篇幅，文中只列出混凝土强度为C20的混凝土随机模拟计算结果的前200项数据。

表1 单一来源蒙特卡罗随机试验计算结果 MPa

3 再生混凝土抗压强度的分布曲线

将表1随机模拟结果及未列出的其他组的模拟结果与再生混凝土抗压试验统计出的数据进行比较，用抗压强度—F(x)平面曲线来表示，单一来源再生混凝土模拟结果与试验结果的对比见图1。

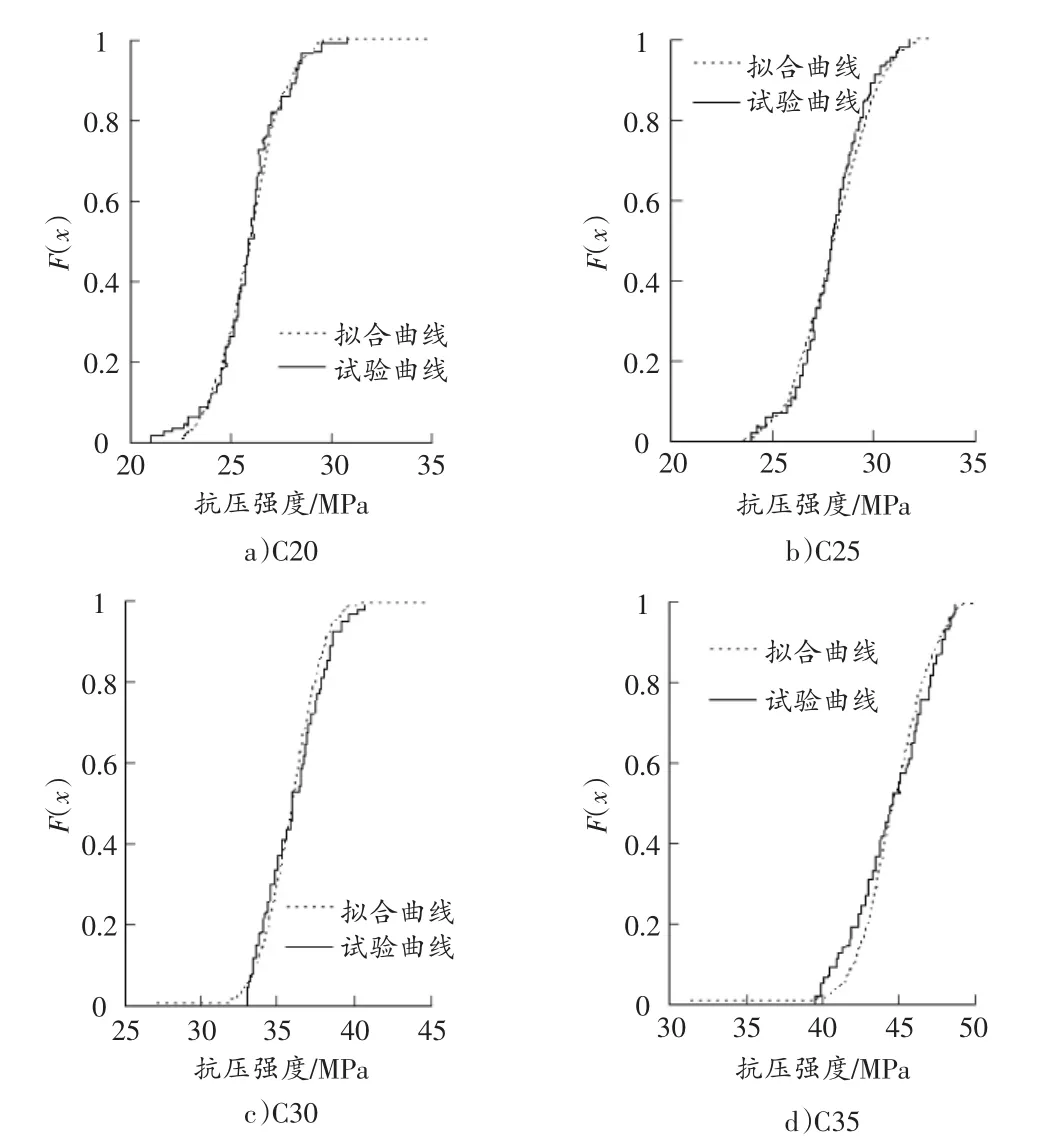
图1 单一来源再生混凝土抗压强度对比

图1表明，单一来源再生混凝土的模拟结果与试验结果非常接近，其中抗压强度为C20，C25，C30的拟合结果与试验曲线十分吻合，C35由于再生骨料的个别因素，其结果与拟合曲线差异相对较大。

4 结语

单一来源再生混凝土抗压强度试验的随机模拟结果与试验结果从整体上分析十分接近，当显著性水平α=0.05时，单一来源再生混凝土抗压强度试验结果的分布特征可以用正态分布模型来描述，为再生混凝土可靠度的研究打下了基础。

［1］ 徐钟济.蒙特卡罗方法［M］.上海:上海科学技术出版社，1985.

［2］ 肖 祥.再生混凝土基本力学性能试验研究［M］.青岛:山东科技大学，2008.

［3］ 王 江，薛燕飞，周 辉.再生混凝土抗压强度研究［J］.混凝土，2006(7):47-49.

［4］ 袁 飚.再生混凝土抗压抗拉强度取值研究［D］.上海:同济大学，2007.

［5］ 叶孝恒.再生混凝土基本力学性能试验研究［J］.西部探矿工程，2007(7):183-189.