频率计算法在常庄水文站的应用实践

□张 允（郑州水文水资源勘测局）

□李卫卫（黄河水利委员会河南水文水资源局）

□姚常慧 □韩瑞瑞（郑州水文水资源勘测局）

一、概况

常庄水文站位于郑州市中原区须水镇常庄水库，流域面积82km2，干流长度27.5km，是贾鲁河支流贾峪河上的重要控制站。该站1980年7月1日由河南省水利厅设立为水库专用站，1984年改为水库水文站，1985年又改为水库水位站。2001年恢复常庄水库专用水文站。随着近年来郑州城市的快速发展，水资源的合理开发利用在城市今后发展中的作用越显重要。特别是1998年常庄水库被确定为郑州市水源地、郑州市应急供水任务地方后，水库经常反向蓄水（从邙山引水到西流湖后反压到水库）且常年处于高水位运行状态，水文站的水文观测对水库防汛预报、水库安全调度运用、城市防洪、水质监测等提供了重要的水文数据，其作用越来越为重要。每遇大到暴雨，当日雨量达到200、150mm时，郑州市领导及市民都会关心地询问，“多少年一遇的大雨啊”？这时可采用数理统计的途径来寻求水文现象的统计规律，从而对未来长期内水文现象的变化情况作出预估，频率计算法是数理统计法中的一个主要内容，也是目前水文计算中用的最多的一种分析计算方法。

二、频率计算

（一）随机变量

实践表明，偶然现象虽有它不确定的一面，但观测大量同类的偶然现象，还是可以发现它的统计规律。由于这种规律是和它的出现机会分不开，因此在数学上称这种偶然现象为随机现象。随机现象可以取得不同的数值，这些数值可以用一个变量来表示，这种变量就叫做随机变量。随机变量的各个数值都对应一定的出现机会。水文计算中的流量和雨量等水文资料都是随机变量，如常庄水文站1980年24h最大降雨量64.0mm就是一个随机变量。

（二）总体和样本

数理统计中，把随机变量的全体，亦即包括整体的系列，称为总体。从总体中任意抽取一部分系列，称为样本。许多水文现象的总体是无限的，实际上也无法取得。例如常庄水文站的年24h最大降雨量，其总体应包括从古至今以至延长到未来无限年代的所有资料。而现在所观测到的几十年24h最大降雨量资料，只不过是总体中的一部分，是一个很有限的样本。

（三）频率

在数理统计中，频率是指随即变量某值在样本中的出现机会（即概率或机率）。在水文计算中，频率则表示等于或大于某一变量可能出现的机会；具体地说，等于或大于某一变量的出现次数与总次数的比之，就称为这个变量的频率。频率通常以百分数表示。例如用常庄水文站30年的实测24h最大降水量资料，将这30年的资料按大小顺序排列，则等于或大于第一个最大雨量值在30年中只有一次，等于或大于第二大的雨量值在30年中有两次，依次类推，则等于或大于最后一个最小的雨量值在30年中共有30次。将这些等于或大于的次数分别除以总次数，所得的百分数便是各个年雨量值所对应的频率，如表所示。

频率常用符号P来表示，P=5%表示等于或大于某变量的出现机会为5%。

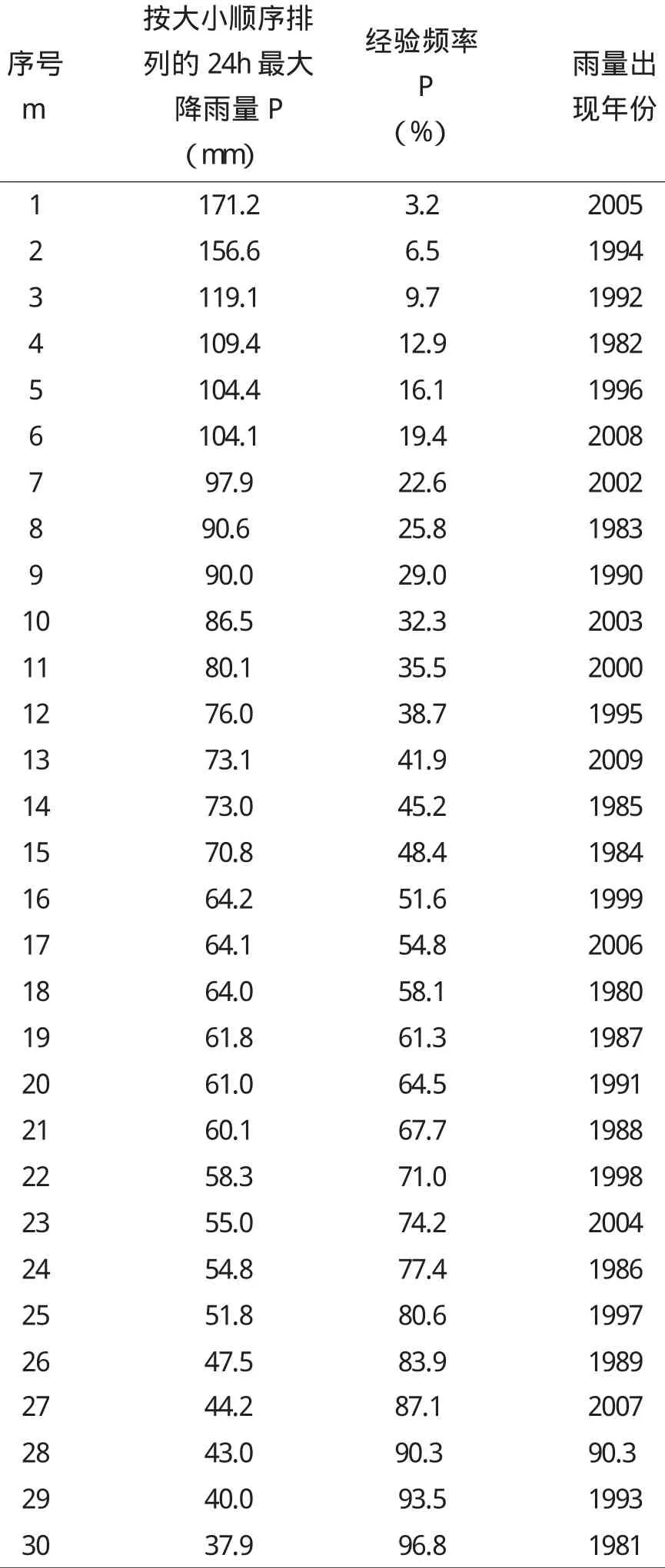
表1 常庄站24h最大降雨量频率计算表

（四）重现期

频率是一个抽象的统计术语，不够通俗。因此，水文计算中经常用重现期来表示随机变量的出现机会。重现期的含义是指平均多少年出现一次。例如P=5%，即平均100年可以出现5次，或平均20年出现一次，亦即重现期为20年，或称20年一遇。重现期常用符号T来表示。

三、经验频率曲线

根据实测水文资料，按从大到小的次序进行排列，然后用经验频率公式计算出来的频率，成为经验频率。以水文变量为纵坐标，以经验频率为横坐标，点绘经验频率点据，根据点群分布趋势，绘出一条平滑的曲线，称为频率曲线。经验频率曲线是根据实测资料（样本）直接绘成的。

（一）经验频率公式

计算经验频率的公式有好几种，目前我国常用计算经验频率公式为：

式中：p—等于或大于某变量的经验频率；

m—系列按递减次序排列时，各随即变量的顺序号；

n—观测资料的总项数。

（二）经验频率曲线

用常庄站1980～2009年实测年24h最大降雨量资料，按表格式计算其经验频率。

表中第（3）栏经验频率是按式（1）计算得出，以表中第（2）栏的24h最大降雨量P为纵坐标，第（3）栏相应的经验频率P为横坐标，在等分格纸上点绘经验频率点据，然后通过点群中间目估绘出一条平滑曲线，即为该站年24h最大降雨量经验频率曲线。

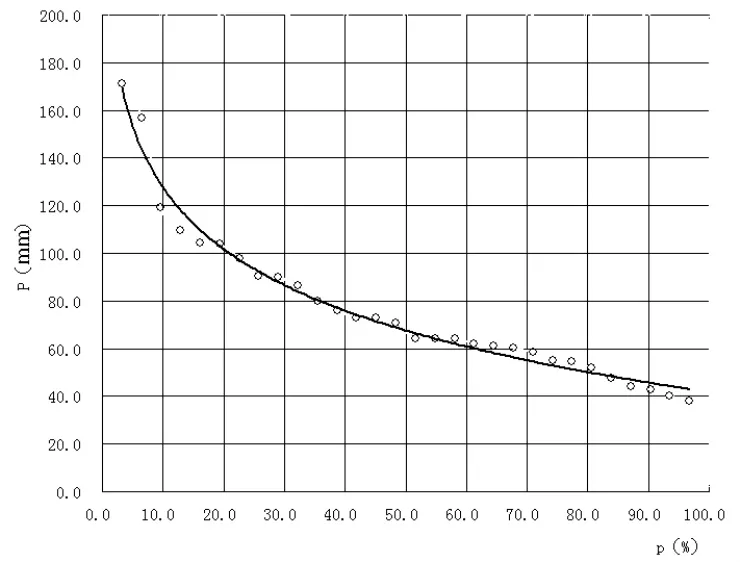
图1 24h最大降雨量经验频率曲线图

（三）频率格纸

绘制并适用经验频率曲线是比较简单的，但经验频率曲线以目估方法绘制，曲线的形状往往因人而异，差别较大。并且在一般等分格纸上，曲线两端的坡度较陡，按曲线趋势外延，任意性较大。曲线外延部分稍有偏离，推求出来的设计数值可能产生很大误差。因此，通常采用频率格纸（亦称机率格纸）来绘制频率曲线，以代替普通的均匀方格纸。

频率格纸是水文计算中绘制频率曲线专用的一种格纸。它的纵坐标为均匀分格或对数分格，表示变量；而横坐标则为不均匀分格，中间部分分格较密，向左右两端分格渐稀，表示频率。在这种格纸上绘制频率曲线，两端的曲线坡度会大大变缓，这对曲线的外延是较为方便的。

四、统计参数

水文系列同各种随机变量的分布情况是不相同的。有的变量数值大，有的变量数值小；有的变量比较集中，有的则比较分散；有的变量呈对称分布，有的则不对称，等等。在数理统计中，用来描述这些特征的数值，称为统计参数。

水文分析计算中常用的统计参数为均值、均方差、离差系数和偏态系数等。

（一）均值

式中:xi—某一变量。

均值表示系列的平均情况。例如，利用式（2）可计算出常庄站的多年平均24h最大降雨量值为77.0mm。

（二）均方差

均值能表示系列的平均情况，但不能说明系列的离散程度。均方差能放映系列的离散程度，通常用符号σ表示，计算公式为：

利用式（3）可计算出样本表1中常庄站24h最大降雨量值系列的均方差为32.0。

（三）离差系数

均值相同的系列，可用均方差来比较它们的离散程度。但当系列的均值不相同时，就不能用均方差来进行比较，必须用相对量即均方差与均值的比值来做比较。这个比值称为离差系数，以符号Cv表示。计算公式如下：

（四）偏态系数

偏态系数也叫做偏差系数，以符号Cs表示。它是反映变量在均值两边是否对称或不对称程度的一个系数。我省范围内一般采用Cs=3.5Cv。

五、皮尔逊Ⅲ型曲线

（一）理论频率曲线

具有一定数学方程式的频率曲线，称为理论频率曲线。有了理论频率曲线，就可以使频率曲线的绘制和外延有一定的依据，改善了目估绘制频率曲线的方法，减少了曲线外延的任意性。

理论频率曲线是根据自然界大量实际资料的分布趋势建立起来的，并不是从物理成因方面推导得出，实际上仍具有一定的经验型。根据我国多年的使用经验，其中能较好的配合水文资料的线型是皮尔逊Ⅲ型曲线，简称P-Ⅲ型曲线。

（二）皮尔逊Ⅲ型曲线的计算公式

皮尔逊Ⅲ型曲线是英国生物学家皮尔逊于1895年根据某些实际资料建立起来的曲线族中的一种线型。皮尔逊Ⅲ型曲线的数学方程式较为复杂，方程中除变量x和频率p以外，还包含三个统计参数，即均值离差系数Cv和偏态系数Cs。为了简化计算，经数学推导后,得出以下简单公式：

式中:xp—频率为p的随机变量；

φ—离均系数，随p和Cs而变，可根据不同的p和Cs查

φ表得出;

Kp—模比系数，， 可根据不同的比值查Kp值表得出。

（三）皮尔逊Ⅲ型曲线的绘制

推求某指定频率p的水文变量xp，可从皮尔逊Ⅲ型曲线中查得，也可以根据三个统计参数、Cv和Cs，从Kp值表中查出Kp值，乘以，即为对应于p的xp值。

由 Cv=0.42,Cs=3.5,Cv=1.47及p=1%，查Kp值表得 Kp=3.18，则百年一遇的24h最大降雨量为：

六、结束语

随着郑州市社会经济的飞速发展，每遇暴雨都将给郑州市带来巨大经济损失，而采用频率分析方法，计算相应站点的暴雨频率，分析雨强特征、暴雨成因，可提高防洪预报的时效性，从而为全市防汛减灾工作提供强有力的服务，最大程度的减少洪涝灾害造成的损失。