基于散射参数法的波导滤波器设计

王 琦

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

波导滤波器是一种成熟的滤波器形式,由于其腔体无载Q值高、损耗小、带外抑制特性好、承受功率大而在电子设备中有着广泛应用。

到目前为止波导滤波器已经有一套经典的设计公式,按照公式,设计师可以完成设计。但是传统的滤波器设计公式只是能够得到一套较为粗糙的数据,设计成型的滤波器优化和后期调试则会耗费大量的时间和精力。随着三维电磁场仿真软件水平的进一步提高,使精确设计滤波器成为可能。

该文提供了一种散射参数法准确设计波导滤波器的方法,应用此方法在目前计算机的主流配置下就可以快速精确地设计、仿真和优化波导滤波器,大幅度地提高设计效率,降低研发和生产成本。这里以带通滤波器为例详细地阐述了滤波器设计的全过程。

1 设计原理分析

1.1 散射矩阵级联

波导带通滤波器,由耦合结构和谐振腔级联而成,如图1所示,其腔间典型耦合结构可以简化成如图2所示的基本单元。

图1 带通滤波器组成

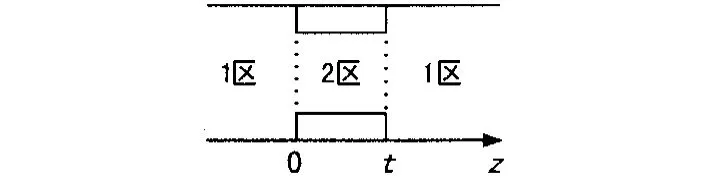
图2 耦合结构基本单元

波导滤波器耦合结构基本单元可以看做为3个二端口网络的级联而成,长度为t的1区及z=0和z=t处的不连续性。2区可以看做成长度为t的传输线。用仿真软件进行计算仿真时,可以把这三区合并为一个结构进行仿真,直接就可以得出需要耦合结构的散射参数值。

分析波导滤波器时,将膜片和销钉等不连续性波导和规则波导等单元按照广义二端口网络处理。典型的2个广义二端口网络级联,级联以后形成新的二端口网络,如图3所示,其级联散射矩阵Sc表示为[1]:

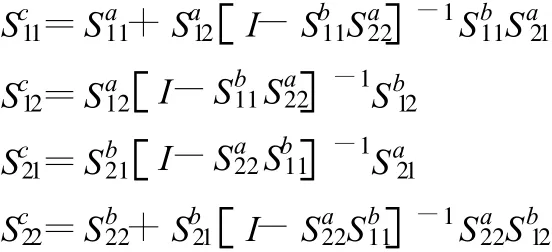
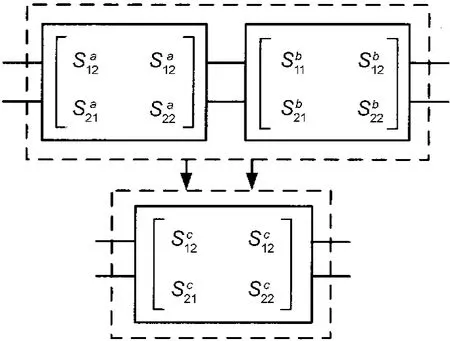
图3 二端口网络散射矩阵级联

1.2 散射参数计算

波导滤波器整体散射矩阵可以看作是由各不连续性波导散射矩阵和规则波导单元散射矩阵交替级联而成。

耦合谐振器带通滤波器,其各个谐振腔之间的耦合结构采用阻抗变换器Ki,j或者导纳变换器Ji,j级联。阻抗变换器的级联矩阵[2]可以写成下式:

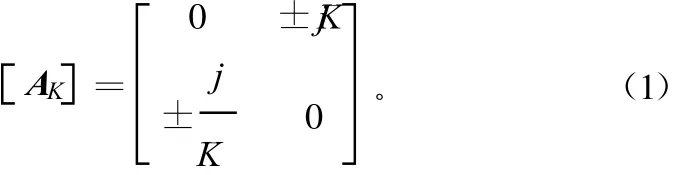
式中,K¯=,当耦合为感性耦合时取负值,当耦合为容性耦合时取正值。阻抗变换器和导纳变换器为对偶关系,可以相互转换,因此在此只讨论含有阻抗变换器的滤波器。

由微波网络中矩阵A矩阵与S矩阵的转换关系,可以得出阻抗变换器的S矩阵。

对于互易网络:

对于对称网络:

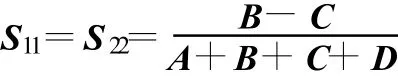
于是可以得出单节阻抗变换器的散射参数矩阵S为:

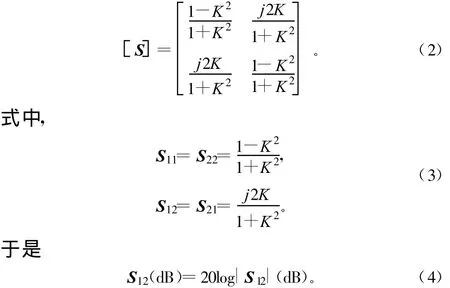
阻抗变换器K可以由式(5)～式(7)得出[3]:

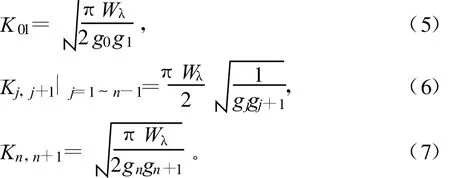
式中,Wλ为带通滤波器的相对带宽;g0,g1…gn,gn+1为归一化低通元件值。

1.3 滤波器仿真

滤波器仿真依据其仿真过程可分为耦合结构散射参数仿真、谐振器长度仿真、滤波器整体仿真3个步骤。

步骤1:耦合结构散射参数仿真。耦合结构的理论设计数据得出之后,在三维电磁场仿真软件HFSS中按照图2所示建模,仿真其中心频率4.91GHz处的S12值。建模时,耦合结构两侧的波导长度不低于四分之一波导波长,直到其S12参数的仿真结果与理论数据相符合,可以得出耦合结构的尺寸。

步骤2:谐振器腔体长度仿真。用相应耦合结构的尺寸在仿真软件建立谐振器模型,如图4所示。更改谐振器的长度,使单腔谐振器的谐振频率与所要求的滤波器通带中心频率一致,即可以算出谐振器的长度。

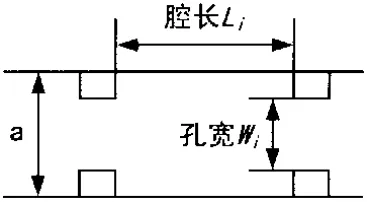
图4 谐振器模型

步骤3:滤波器整体仿真。把所有的耦合结构和谐振器按照图1所示结构交替级联起来,利用步骤1和步骤2的仿真数据,对滤波器进行整体仿真优化,完成滤波器设计。

2 设计实例

设计一个 5腔波导带通滤波器,通带频率4.82～5.0 GHz,要求通带内插入损耗小于0.5 dB,回波损耗小于-20 dB。

选择切比雪夫型低通原型,滤波器通带波纹为0.01 dB,耦合结构采用电感膜片,波导选用标准BJ48波导(a=47.549 mm,b=22.149 mm),取膜片厚度为1 mm,其设计过程及归一化元件值如下:

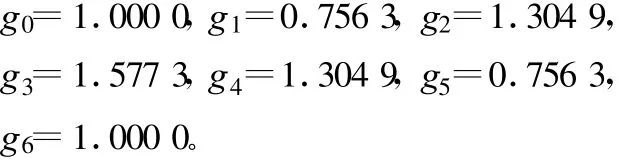
频率4.82 GHz的波导波长分别为为 λg1=82.3 mm;频率5.0 GHz的波导波长分别为 λg2=77.3 mm。

波导滤波器通带中心的波导波长由下式算出:

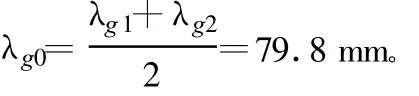
由此可得波导带通滤波器的相对带宽:

把相对带宽Wλ和归一化元件值值代入式(5)～式(7),可求出各阻抗变换器K值

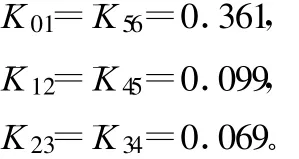
将以上数据代入式(4),可得出每一节耦合结构的S21值:

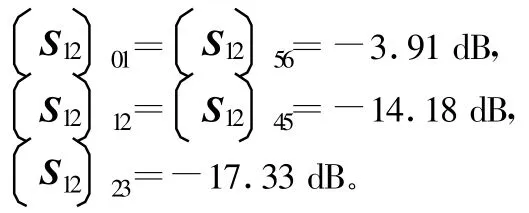
依据耦合结构的理论设计数据,在三维电磁场仿真软件HFSS中按照图2所示建模,仿真其中心频率4.91 GHz处的S12值,直到仿真结果与理论数据相符合。注意在建模时,耦合结构两侧的波导长度不低于四分之一波导波长。通过以上仿真,可得出耦合孔的宽度:

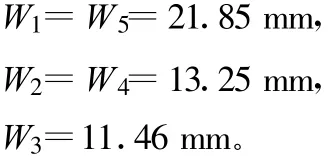
按照图4在HFSS中建立谐振器仿真模型,其耦合结构按照上一步中得到的耦合结构数据建立模型,然后更改谐振器的长度进行仿真,使谐振器谐振频率为4.91GHz,此时谐振器的长度即为所需的数据。

最后将耦合结构与谐振器级联起来仿真,可得到整个滤波器的幅频特性曲线,如图5所示。此曲线未经优化,完全是设计值。从图5中可以看出滤波器幅频特性曲线已经比较理想,通带内回波损耗小于-20.8 dB,各项指标已满足设计要求,只需稍加调整便可得到更加理想的幅频特性曲线。

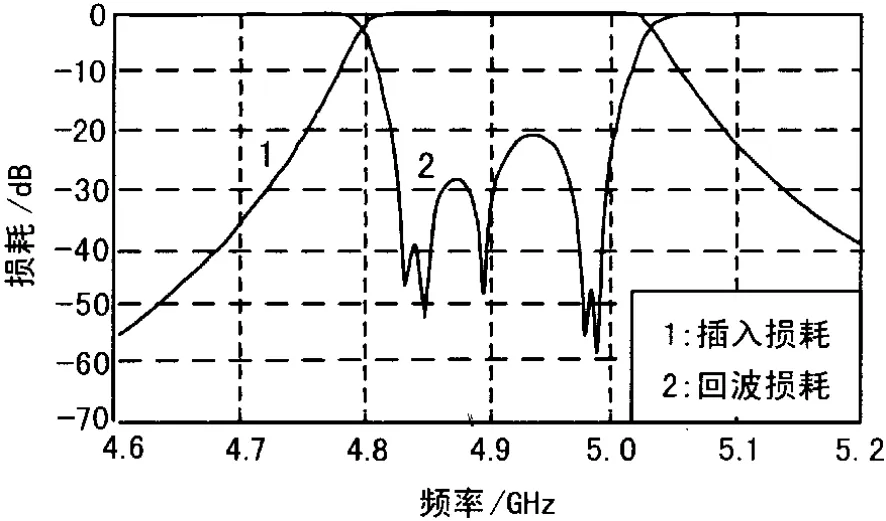
图5 仿真曲线(未优化)

3 结束语

通过设计实例可以看出,用散射参数法设计的波导带通滤波器的理论设计与仿真曲线较吻合。如果在设计时注意加入频率修正,并且加工精度能够保证,则波导带通滤波器完全可以做到减少90%以上的调试量甚至免调试。经过工程的实际验证,采用散射参数法设计的波导滤波器与仿真结果非常一致;同时将散射参数法推广到了可调滤波器的设计中,取得了很大突破。

散射参数法可以直观得出耦合结构的幅频特性趋势,与设计需求相结合,精度高,为设计波导滤波器提供了一种准确的设计方法,提高了设计效率和设计精度,大大减少了后期调试成本,具有很高的推广应用价值。

[1]张本全.微波无源器件设计中的模式匹配法研究[D].成都:电子科技大学.2004:17-18.

[2]林为干.微波网络[M].北京:国防工业出版社,1978.

[3]甘本祓,吴万春.现代微波滤波器的结构与设计[M].北京:科学出版社,1973.