改进的非相干信号子空间宽带测向算法
宫 兵,徐以涛,李 佳
(解放军理工大学通信工程学院,江苏南京210007)
0 引言
宽带信号是电子侦察常见信号之一,对其进行测向是电子侦察的主要任务[1]。近年来有关宽带源方位的估计愈来愈受到人们的关注。非相干信号子空间方法[2](ISM)是最早提出的宽带信号的测向算法,其思想是通过频域变换将时域信号分解成不同频率的子带,在每个子带上分别应用窄带信号测向算法,然后再对不同子带的测向结果进行平均得到宽带信号的方位估计。由于在某些子带信号的功率会非常低导致这些子带的会对最终测向结果造成较大的误差,从而影响测向精度。为此文献[3]提出了基于聚焦变换思想的相干信号子空间算法(CSM),其中聚焦矩阵的求解是算法的关键。随后文献[4]等文献分别介绍了几种不同的聚焦矩阵的求解方法对CSM算法进行改进,然而聚焦矩阵的计算也是不小的计算量。这里提出了一种基于最大功率进行频点选择的改进的ISM算法,称为MISM算法,它不需要像ISM算法在每个频点都要进行窄带信号测向算法,也不需要像CSM算法进行聚焦矩阵的计算,大大减小了运算量,提高了测向精度。
1 阵列结构和信号模型
考虑有m个阵元的均匀线阵,阵元间距为p,令左边第一个阵元为参考阵元,如图1所示。
假设有d(d<m)个远场宽带不相干信号进入阵列,其到达角分别为 θ1,…,θd,并假设信号和噪声具有相同的带宽B,并且阵元输出噪声是空时统计独立的、零均值的和方差为 σ2的高斯白噪声,且与信号不相关。于是,第i个阵元上接收的信号可表示为:

式中,sk(◦)为在任意参考点接收的由第k个信源发射的信号;τik为第i个阵元对第k个信源的传播延迟;aik为第i个阵元对第k个信源的幅度响应;ni(◦)为第i个传感器上的加性噪声。对于均匀线阵,传播延迟可表示为:
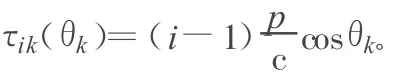
式中,c为传播速度。因为sk(◦)为宽带过程,所以在频域表述这一问题更方便。假设观测时间间隔为T,ri(t)可用傅里叶系数表示为:

式中,Ri(ωn)为傅里叶系数,表示为:
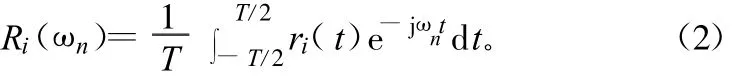
假设观测时间远大于信号掠过阵列的传播时间,式(1)两端用傅里叶系数表示后得到:

用矩阵表示即为:

式中,R(ωn)和N(ωn)是m×1的矢量,

S(ωn)是d×1的矢量,ST(ωn)=[S1(ωn)…Sd(ωn)],并且A(ωn)是m×d的矩阵,

注意到A(ωn)的每一列与不同的信源相关联,故可把列矢量表示为a(ωn,θk)(k=1,…,d),并称为信源的方向矢量,假设A(ωn)满秩。
将式(3)乘以它的转置并求期望得到:
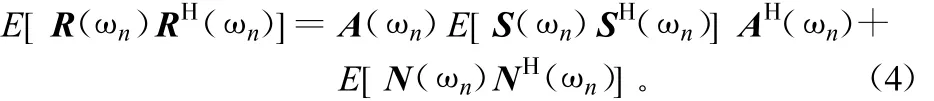
式中,H代表哈密特转置。假设噪声互不相关并且有相同的频谱密度矩阵,可将式(4)改写为:

式中,K(ωn)和P(ωn)分别为过程和的频谱密度矩阵;σ2(ωn)为噪声的频谱密度矩阵,并假设P(ωn)是非奇异的。
2 ISM算法
ISM算法是基于频谱密度矩阵K(ωn)的特征分解的算法,它假设以下条件成立:
①信号的频谱密度矩阵P(ωn)是非奇异的;
②任意d+1方向矢量是线性独立的。
在这些条件下,K(ωn)的特征值 λ1(ωn)≤…≤λm(ωn)和特征矢量V1(ωn),…,Vm(ωn)有以下性质:
①K(ωn)的最小特征值为 σ2(ωn),并且重数为m-d,即
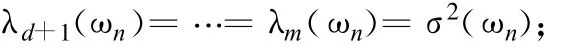
②最小特征值对应的特征矢量与列矢量是正交的,即

注意到式(5)或式(6)的正交关系对于带宽B内的任意一个频点ωn都成立。根据正交关系,信源数目可以由频谱密度矩阵K(ωn)的最小特征值的重数来估计,K(ωn)的估计值为:
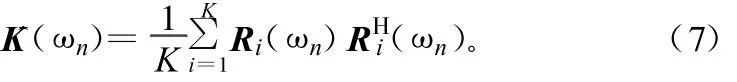
式中,Ri(ωn)为对应频点 ωn处的第i个时域子间隔的傅里叶系数矢量;K为子间隔的数目。
用l1(ωn)≥l2(ωn)≥…≥lm(ωn)和C1(ωn),…,Cm(ωn)分别表示频谱密度矩阵估计值的特征值和特征矢量,故其最大似然估计可表示为:

然后找到^d个最接近正交于矢量集{^V^d+1,…,^Vm}的θk,即为信源DOA。对各频点和整个频率范围均使用算术平均可得到估计子:

对各频点使用算术平均而对整个频率范围使用几何平均可得到估计子:

对于角度范围进行搜索,找到^d个峰值对应的角度θ1,…,θ^d即为信源方位。
3 MISM算法
用Fs表示抽样频率,观测时间T内的抽样数目为:

时间T内的抽样称为一次“快拍”,假设有K次快拍,整个抽样时间即为T1=KT,于是式(2)变为:

即为第i个传感器在第k个频点处的第kk次快拍,于是得到:


式中,J为带宽B内的频点数。为了说明MISM算法,定义频点功率为:
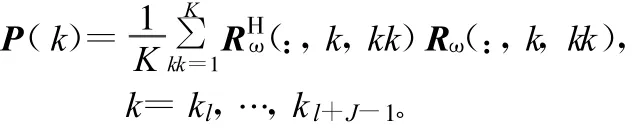
然后是找到最大功率对应的k值,即
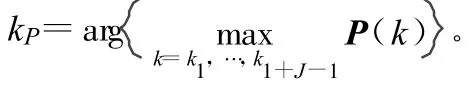
于是,式(7)和式(8)分别变为:

式(9)即用来计算特征值和特征矢量。可以看到MISM算法仅仅需要一次特征分解而ISM需要J次。
4 仿真实验
阵列为均匀线阵,由16个各项同性的阵元组成,阵元间距为信号中心频率的半波长。考虑2个带宽相同的宽带信源,中心频率为100 Hz,相对带宽为40%,抽样频率为240 Hz,假设信源方位角分别70°和75°。信号观测时间为 26.67 s,应用式(10)的估计子,并且K=100,N=64。
4.1 分辨概率分析
根据上述仿真条件,信噪比为[-15∶15]dB,进行100次蒙特卡罗仿真得到2种方法的分辨概率如图2所示。

图2 分辨概率
由图2可知,从总体上看,在-2.5 dB以上,MISM算法的分辨概率大于ISM算法的分辨概率,在-2.5 dB以下,ISM算法分辨概率较高。ISM算法在10.5 dB达到100%的分辨率,而MISM算法在1 dB时即可达到100%分辨率,因此新算法所需的信噪比门限低。在实际应用中,信号在-2.5 dB以上很容易满足,因此MISM算法具有实用价值。
4.2 误差分析
假设信噪比为[-15∶15]dB,对2种算法的方差进行100次蒙特卡罗仿真得到方差图如图3所示。

图3 70°和75°的2种算法方差图
由图3可以看出,对于70°信源,MISM 算法比ISM算法方差要小4(degree×degree=de2)以上;对于75°信源,当信噪比大于1 dB时,MISM算法比ISM算法方差要小1(de2)左右,信噪比小于1 dB时,2种算法方差之差在减小,在-5 dB时差别还比较大,这是因为此时2种算法的分辨概率均较低,不能准确地分辨2个信源。
5 结束语
上述提出了一种基于最大功率进行频点选择改进的非相干信号子空间算法,不需要在每个频点都进行窄带信号测向算法,也不需要进行聚焦矩阵的计算,大大减小了算法运算量,提高了测向精度。对文中算法进行了仿真验证,从仿真结果可以看出,新算法具有更低的信噪比门限和更低的测向误差。可见文中算法具有一定的工程实用价值。
[1]谢 诺,葛建华,窦修全.基于ESPRIT宽带信号测向技术研究[J].无线电工程,2009,39(12):17-19.
[2]WAX M,SHAN T,KAILATH T.Spatio-temporal Spectral Analysis by Eigenstructure Method [J].IEEE.TransactionASSP-32,1984(8):817-827.
[3]WANG H,KAVEH M.Coherent Signal-subspace Processing for the Detection and Estimation of Angles of Arrival of Multiple Wide-band Sources[J].IEEE.Transaction.ASSP-33,1985(8):823-831.
[4]VALAEE S,CABAL P.Wideband Array Processing Using a Two-sided Correlation Transformation[J].IEEE.Transaction.ASSP-43,1995(1):160-173.
[5]张贤达.现代信号处理[M].北京:清华大学出版社,2002.
[6]李石岗,丛玉良,张旭利.宽带信号DOA估计的一种快速算法[J].吉林大学学报,2009,27(1):1-5.
——以鲁甸地震相关新浪微博为例

