大规模短文本的不完全聚类

彭泽映，俞晓明，许洪波,刘春阳

(1. 中国科学院 计算技术研究所，北京 100190； 2. 国家计算机网络应急技术处理协调中心，北京 100029)

1 引言

聚类分析[1](非监督学习)是数据挖掘中的一个重要领域。它将大量具有相同属性的事物按照相似度分为各个组，进而辅助人们从这些信息中抽取摘要或者发现新的规律。至今，聚类分析已成功应用于文本摘要、生物基因识别、电子商务客户行为分析等众多方面、取得了很好效果。

随着这两年Twitter带来的新一波内容风潮，越来越多关注被投放到了一种早已广泛存在的信息形式： 短文本。称之为短文本是因为这些信息都是一些很短的文本，一般字数都不超过100。实际上，在Twitter风靡之前，短文本就早已深入人们的网络生活中，甚至可以说是与网民最贴近的信息形式。搜索引擎中与用户最相关的部分用户查询就是一种典型的短文本； “网络固话”即时通讯软件中的聊天对话基本都属于短文本。除此之外，聊天室对话、新闻标题、论坛标题和SNS状态信息等也都是短文本的栖息地。另外，人们日常生活中的得力交流助手短信，也是短文本的巨型源泉。

短文本在传递公开信息的同时携带了丰富的用户信息，从而成为一种新的具有极大价值的信息资源，对于此类数据的聚类需求也凸现出来。

应用场景一： 网络热点信息的发现。通过对网络上的短文本信息进行聚类，可以挖掘网络上的热点信息，帮助用户更好地获取和理解网络信息。

应用场景二： 企业信息系统的改善。对即时通信数据进行分析和挖掘对于企业信息系统的组织和优化具有重要作用。

应用场景三： 关键信息的提取。政府或组织采集的民意调查数据包含了民众对社会事件的看法、观点等舆情信息。情报工作者需要对大量短语消息进行采集和处理，以发现可疑的对话和人，通过监测公共开放聊天室的会话，利用聚类技术可以自动提取与违法行为相关的对话或行为模式。

至今，已有许多聚类算法被相继提出，但常用的文本聚类算法如K-means等在短文本聚类中效果不佳[2]。主要是因为短文本一般具有以下特征：

a. 形式不规范，趋向口语化。很多短文本都带有很多口语化内容和网络流行语，还有一些使用变形字，如“我”变“额”。

b. 短文本特征信息很少，只有少量的字可以被分析使用。

c. 数量巨大，通常至少是百万级的。

d. 实时性要求较高，因为短文本是不断的产生的，而且信息更新很快，如Twitter上的信息，基本上每个小时都有热点话题产生。

近几年来也有一些专门针对短文本的聚类算法被提出，代表性工作有： Wang等针对即时通信消息的聚类提出了WR-Kmeans算法[2]，He等提出了一种基于中文块的中文短文本聚类方法[3]，黄永光等提出一种采用检索思想的短文本聚类算法[4]，贺涛等提出一种基于免疫的中文网络短文本聚类算法[5]，这些工作主要是针对上面提到的短文本的a、b特征进行的研究，在一定程度上提高了短文本聚类的效果，但并没有在聚类性能上做太大改进。

而实际应用中的短文本信息往往具有很大的数量，这些信息在短时间内都可以达到上千万甚至过亿的量级。以Twitter为例，Twitter每天产生的信息量可以达到6 500万条，且这个数量仍在不断增加[6]。已有的针对短文本的聚类方法在大规模数据上的处理性能往往达不到实际应用的要求。

本文通过对实际应用中的短文本信息进行深入观察和实验分析，发现这些大规模短文本的类别具有“长尾现象”，并据此提出一种新的不完全聚类的思想，可以很大程度上解决聚类的性能问题。

2 背景知识

聚类分析指将物理或抽象对象的集合分组成为由类似的对象组成的多个类的分析过程。常用的文本聚类分析方法主要包括分割式聚类法、层次聚类法。本节对这两种常用的聚类算法加以介绍，并对它们在短文本聚类中的应用进行相关分析。

2.1 分割式聚类法

分割式聚类法的中心思想是： 通过不同的重分配策略不断优化已存在的类别。分割式聚类算法一般是迭代算法，在迭代的每一步对类别进行优化。最典型的分割式算法是K-Means算法。

K-Means算法[7]是目前在科学和工业领域应用最多最广泛的聚类算法，它的算法流程如下：

步骤1. 从所有数据对象中选取K个数据对象作为初始聚类中心；

步骤2. 对其他数据对象，根据其与聚类中心的距离，分配给各个类别；

步骤3. 根据分配结果，取每个类别所有数据的平均值，作为新的聚类中心；

步骤4. 迭代运行步骤2和步骤3，直到所有的聚类中心不再发生变化。

K-Means算法具有流程简单直观、复杂度低，效率高、算法易于并行等优点。但同时该算法也存在以下一些固有缺陷：

a) 需要预先给定聚类数目K，K的设定对算法结果影响较大；

b) 初始K个中心点的选择对算法准确度有较大影响；

c) 算法对outliers非常敏感。

对于短文本聚类，短文本类别数量巨大，类簇的个数K难以预先给定，更不用说K个初始中心点的选择。另外，虽然K-Means聚类算法相比于其他聚类算法具有较高的效率，但对于巨大数量的短文本，K-Means迭代过程所需要的运行时间通常也是难以接受的。

另一种常见的分割式聚类法是K-Medoids算法。基本思路和K-Means是一样的，不同的只是中心点的选择策略，K-Medoids不是取所有点的平均值为中心点，而是取到类别所有点距离和最小的样本点作为中心点，这样K-Medoids就可以用于处理K-Means无法适用的Category类型数据。K-Medoids复杂度比K-Means还高，对于处理短文本性能同样无法接受。

2.2 层次聚类法

层次聚类法[8]可以分为从上至下(分治)和从下至上(聚合)两种方式。从上至下算法起初把所有点看成一个类别，然后根据一定的标准分割类别，直到满足停止条件。从下至上则与此相反，算法起初把所有点分别看成一个类别，之后根据一定标准把若干个类别合并为一个类别，直到满足停止条件。层次聚类法的优点在于聚类结果可以用树状图直观表示，非常适用于本身具有分层结构的数据集。它的缺点主要是需要人为给定停止条件，并且它的时间与空间复杂度均为O(n2)。

层次聚类法的代表算法有： BIRCH算法、CURE算法、CHAMELEON算法等，它们之间的区别基本就在于对不同的连接标准(linkage metric)的选择。连接标准就是拆分类或合并类时的标准。最常用的三类连接标准是： Single link(两个类别之间点的最小距离)、Complete link(两个类别之间点的最大距离)、和Average link(两个类别之间点的平均距离)。

层次聚类算法较高的时间与空间复杂度使其无法应对实际应用中大规模的短文本聚类需求。

3 大规模短文本类别的“长尾现象”

在大部分的聚类算法中，孤立点都是一个不容忽视的因素，有些算法对孤立点很敏感，如K-Means算法。现在已有很多学者针对孤立点的检测和减少孤立点对聚类算法的影响开展研究。但是这些研究可能都基于一个假设： 孤立点相对于正常点是少量的。这个假设对于大多数聚类问题是成立的，但对于手机短信息、Twitter信息、聊天信息等大规模短文本的这些应用场景来说，不一定成立。有很多情况下，孤立点的数量往往大于正常点。这里所说的孤立点不仅指单个的点，也包括数量极小的类别，我们根据这个特征发现这些应用中的短文本的类别往往具有“长尾现象”。

“长尾现象”是统计学中Power Laws[9]和帕累托(Pareto)分布特征的一个口语化表达。长尾现象的示意图如图1所示。举例来说，我们常用的汉字实际上并不多，但因出现频次高，所以这些为数不多的汉字占据了图1广大的灰色区域；绝大部分的汉字难得一用，它们就属于黑色区域的长尾。虽然长尾部分使用频率低，但是由于长尾的“长”，长尾部分的面积甚至会大于灰色区域的面积。

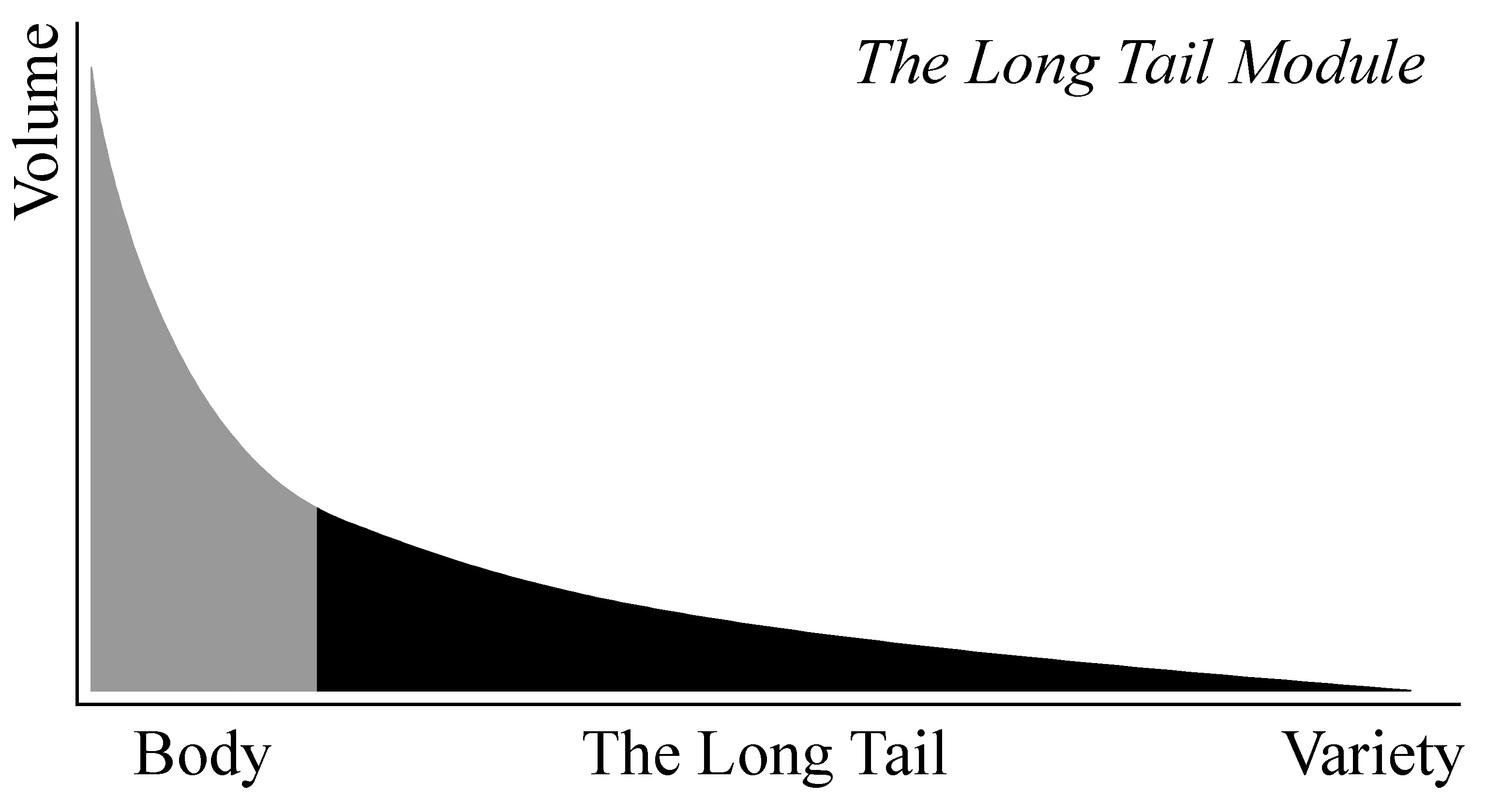
图1 长尾现象

大规模短文本类别的“长尾现象”是指在很多短文本实际应用环境中，有相当部分的短文本类别包含的短文本数量很小，属于孤立点，不太具有聚类的效果和意义，但是它们在短文本总数量中却占据很大比例。仅有少量的类别属于大类别，这些大类别所包含的短文本数很大，是我们通常意义上的“热点”，这些热点才是我们在短文本聚类应用中所真正关注的。以Twitter信息为例，Twitter上的大部分信息属于个人信息，如自己的想法，遇到的事等等，这些信息极少有类别的概念，因此也就缺乏聚类的意义，而当网络出现一些热点事件时，会有很多围绕这些热点的Twitter信息出现，这些信息构成的大类别才是短文本聚类希望得到的结果。

我们通过一个实验对短文本类别的长尾现象进行了验证。我们从Twitter一段时间的数据中收集了98 122条短文本信息。对该数据利用传统K-Medoids算法进行聚类分析，观察聚类结果。试验中类别个数K设为10 000，聚类结果如图2所示。图中，横坐标为聚类类别编号，纵坐标表示该类别中所含的样本个数。从图2可以看出， 该数据中部分样本构成了较大的类簇，这些类簇所体现的信息是我们对短文本进行聚类分析想要得到的热点信息。同时，还有相当一部分文本信息形成了孤立点，也就是长尾现象中的“尾部”。

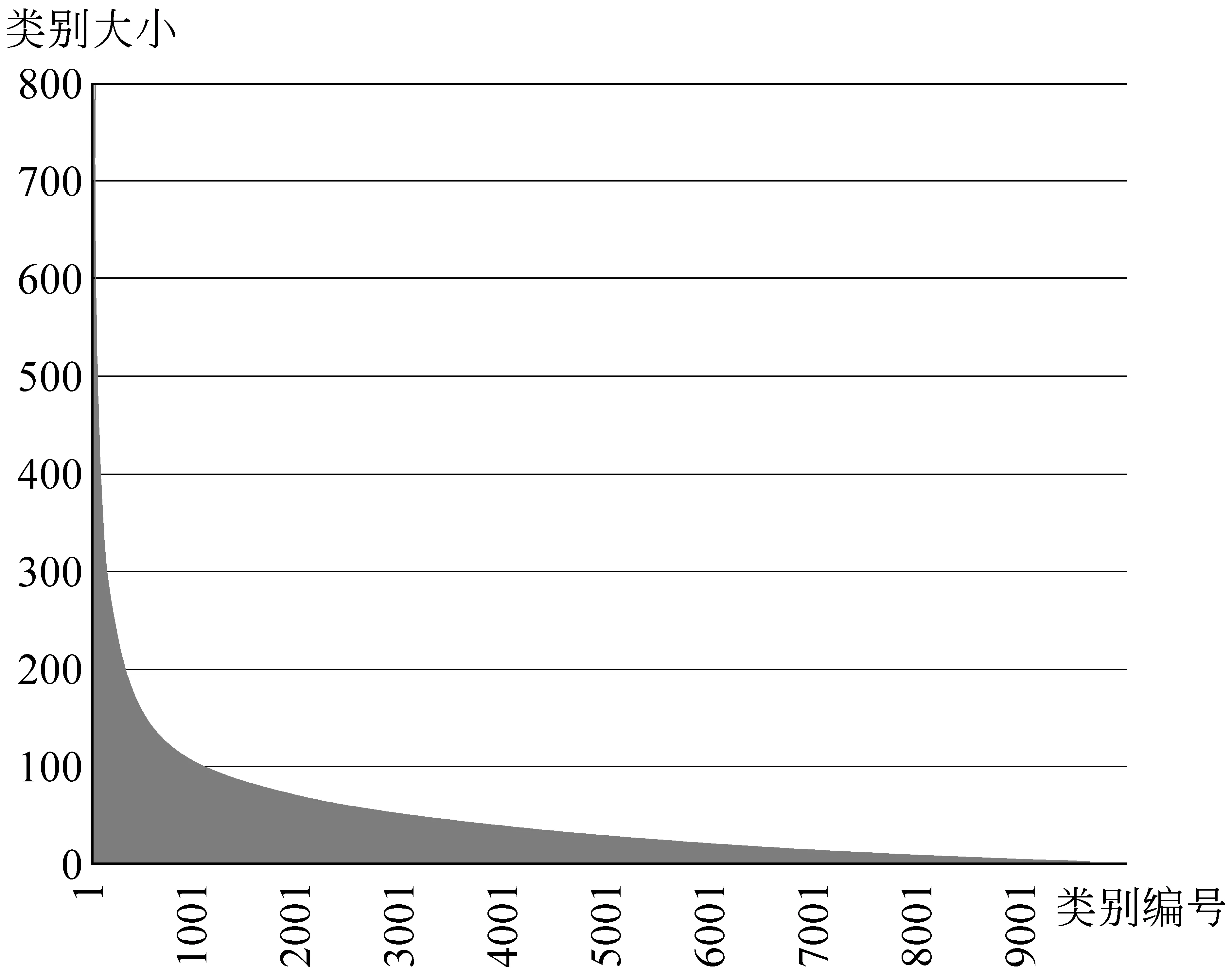
图2 短文本类别柱状图

另一方面，我们对相同的数据采用Single-Pass完全比较聚类算法进行聚类分析，即每个短文本与所有已有类别进行相似度比较，相似度大于一定阈值即将此短文本归于这个类别，如与所有类别均不匹配，则将此短文本新建为一个类别。聚类后对结果进行统计，得到表1所示结果。

表1 短文本聚类结果分析

其中，大类别指样本个数超过10的类别，小类别指样本个数小于3的类别，孤立点指样本个数为1的类别。从表1可以看出，在98 122条短文本样本中，有62 960条样本属于孤立点，超过了总样本数的60%，而大类别数仅有570个，包含的短文本样本数占总样本个数的比例不到30%。

4 大规模短文本不完全聚类

传统的基本聚类算法进行聚类时，大都会对所有数据进行完全聚类，即每个数据最后都会归于一个或多个类别中，我们把这类聚类算法统称为完全聚类。然而，根据第3节的分析，诸如Twitter等具有“长尾现象”的大规模短文本信息中往往存在大量的孤立点文本。这些文本的存在，一方面使得如K-Means等对于孤立点敏感的聚类算法难以适应于这类文本信息的聚类分析。另一方面，这些大量的孤立信息往往并非我们在聚类分析中关注的重点。将完全聚类算法应用于这类聚类问题，算法会将大量运行时间浪费在在缺乏意义的孤立点的聚类上，导致了算法的低效。为此，我们提出了一种新的聚类思想——不完全聚类。

4.1 不完全聚类的主要思想

不完全聚类的主要思想在于在聚类过程中集中资源处理重要的大类别短文本，减少资源在孤立点聚类上的浪费，尽量减少小类别短文本的聚类时间，增加大类别短文本聚类的机会。

依据不完全聚类的思想，可以有多种具体实现方式，本文提出一种基于限制比较次数的不完全聚类算法，此算法主要针对短文本有时间顺序的应用，而大部分实际短文本聚类应用具有此类属性。

4.2 基于限制比较次数的不完全聚类算法

基于限制比较次数的不完全聚类算法通过限制样本与类别之间的比较次数来实现不完全聚类。假设在聚类过程中已经存在n个类别，对于待处理的每一条样本，仅将该样本与根据一定方法选取的m个已有类别进行比较，若与其中某一类别相似度大于一定阈值，则将该样本归属于这一类别，否则将该样本作为聚类中心构成一新类别。待比较的m个类别的选取方法可以有多种，这里我们采用的是选取最新生成的m个类别。采用这种选取方法的原因是在实际应用中短文本的出现具有一定的时间内聚性，即在相同一段时间内产生的短文本更有可能属于同一类别，这是因为一个热点事件发生后，通常会在短时间内产生大量与此事件相关的短文本，而随着时间推移，这类短文本会越来越少。

基于限制比较次数的不完全聚类算法的必然代价是它可能使一些本该聚在一起的样本错失聚类机会。因此，我们在算法过程中加入其他方法减少这种代价。

4.2.1 初始类别的选取

根据上面提到的短文本的时间内聚性，我们选取上一个单位时间段的大类别作为当前时间段聚类的初始类别。例如，如果聚类过程是以小时为单位时间来进行的，那么可以选取上一个小时聚类过程得到的大类别来作为这一个小时的初始类别。当然，在整个聚类过程最初运行时，初始类别就由短文本聚类先后次序决定了。

4.2.2 短文本的排序

为了进一步减小聚类时短文本与已有类别的比较次数，同时让每个短文本尽可能在有限的m次与已有类别的比较中找到属于自己的类别，可以采用对短文本排序的方法来增加短文本之间的空间内聚性，即让更相似的短文本在聚类的先后次序上也更接近。因为在聚类时，每个短文本是与最新生成的m个类别进行相似度比较，假设某一个短文本没有找到归属类别而成为一个新类别，那么与这条短文本相似度更高的短文本如果在聚类的次序上离它更近的话，那这些短文本也就能更快地找到归属的类别，这样既能提高算法的性能，同时也能提高算法的效果。

我们采用的排序方法是，先生成一个固定的短文本模型，让每个短文本与这个模型进行相似度计算，再结合这个相似度值及每个短文本的hash值对短文本进行排序。

4.2.3 m值的自适应选取

对于m值的选取，除了可以使用固定值外，也可以采用更为灵活的自适应选取方法，综合考虑现有类别数，每条短文本属于孤立点的概率等因素来针对每条短文本采用不同的m值。其中，短文本属于孤立点的概率可以根据短文本长度、每个字的df值等内部属性，或者短文本来源等外部属性，利用机器学习方法获取。若能通过机器学习方法获得一个模型来评估每条短文本属于孤立点的概率，会对整个算法的性能和效果有很大的改进。

4.2.4 类别的清理与调整

随着聚类过程的进行，在聚类中产生的类别会越来越多，为了减小孤立点对聚类的干扰，也为了减少聚类过程中内存的占用，我们可以定时对类别进行清理，原则是将陈旧或者数量很小并且没有形成大类别潜力的类别清除。清除后还可以调整特别“热”的事件类别的位置，使后续的短文本更多的与这些“热”事件类别进行比较。

4.3 算法描述

基于限制比较次数的不完全聚类算法的具体流程如下：

步骤1. 选取m个初始类别；

步骤2. 将需要聚类的短文本进行排序；

步骤3. 对每一条短文本，将其与最新生成的m个类别进行相似度比较，如与某一类别相似度大于一定阈值，则将该短文本归于该类别，并更新该类别信息，否则根据该短文本新建一类别，并以该文本作为该类别聚类中心；

步骤4. 对短文本类别进行清理和调整；

步骤5. 如果m不是固定值，则对m进行自适应选取。

在实际的在线短文本聚类分析应用中，将实时采集的单位时间段内的短文本依据上述步骤进行处理即可。

5 实验分析

使用第三节实验中的98 122条短文本数据，对完全聚类和基于限制比较次数的不完全聚类的性能和效果进行比较。完全聚类使用的算法流程与基于限制比较次数的不完全聚类相同，但在进行比较时没有比较次数m的限制。实验结果列于表1中。其中，总比较次数指聚类过程中短文本与类别的总比较次数之和，总类别数是指聚类最终得到的类别个数，大类别数指聚类结果中样本数大于10的类别个数，小类别数指样本数小于3的类别个数，孤立点数指样本数为1的类别个数。

表2 完全聚类与不完全聚类的比较

从表2可以看出，当取m=10 000进行不完全聚类时，聚类所得到的大类别数为569，仅比完全聚类所得到的大类别数少了1个。也就是说，m=10 000时的不完全聚类，几乎能够获得完全聚类所得到的全部大类别。而算法的运行时间与总比较次数均较完全聚类有显著减少。当m取1 000进行不完全聚类时，算法仅需完全聚类7%(31/432)的时间代价即可得到完全聚类80%以上(459/570)的大类别。由此可见，对于具有长尾现象的短文本进行聚类分析时，采用不完全聚类法能够有效地缩减小类别和孤立点所耗费的聚类时间，从而在不丧失聚类效果的前提下大幅度提升聚类算法的效率。

表3 不完全聚类中使用类别清理的结果

在上面实验的基础上，我们对不完全聚类中是否进行类别清理的结果作了比较。类别清理的策略为： 设置最大类别数MAX_CLUSTER_NUM和基类别数BASE_CLUSTER_NUM，当聚类过程中类别数达到MAX_CLUSTER_NUM时，就将类别按照类别大小排序，取类别大小最大的前BASE_CLUSTER_NUM个类别做后续聚类，其余的类别直接清除。实验中m取10 000，MAX_CLUSTER_NUM取10 000，BASE_CLUSTER_NUM取1 000。实验结果如表2所示。从表3可以看出，使用类别清理后，算法仅需40%(87/212)的时间代价即可得到95%(545/569)的大类别数。由此可见，使用类别清理策略可以对不完全聚类算法的效率有很大的提升。

6 结束语

本文对实际应用中的大规模短文本聚类问题进行了研究。通过观察和分析发现大规模短文本类别所具有的“长尾现象”，并提出了不完全聚类思想对具有“长尾现象”的这类数据进行聚类分析。实验结果表明，本文所提出的基于限制比较次数的不完全聚类算法能够快速有效地得到样本信息中的大类簇，是一种处理大规模短文本聚类应用的有效方式。

[1] A.K. JAIN, M.N. MURTY, P.J. FLYNN. Data Clustering: A Review[J]. ACM Computing Surveys, September 1999, 31(3).

[2] Wang L, Jia Y, Han W H. Instance message clustering based on extended vector space model[EB/OL]. Proceedings of 2ndIternational Symposium on Intelligence Computation and Applications. Wuhan, China: Springer, 2007: 435-443.

[3] He H, Chen B, Xu W R, Guo J. Short text feature extraction and clustering for web topic mining[EB/OL]. Proceeding of the 3rdInternational Conference on Semantics, Knowledge and Grid. Washington D. C., USA: IEEE, 2007: 382-385.

[4] 黄永光，刘挺，车万翔，胡晓光. 面向变异短文本的快速聚类算法[J]. 中文信息学报，2007, 21(2): 63-68.

[5] 贺涛，曹先彬，谭辉. 基于免疫的中文网络短文本聚类算法[J]. 自动化学报2009, 35(7).

[6] http://tech.ifeng.com/internet/detail_2010_06/09/1600761_0.shtml[DB/OL].

[7] HARTIGAN, J. and WONG, M. Algorithm AS136: A k-means clustering algorithm[J]. Applied Statistics, 1979，28: 100-108.

[8] Horatiu Mocian. Survey of Distributed Clustering Techniques[EB/OL]. 1stterm ISO report, 2009.

[9] M. E. J. Newman. Power laws, Pareto distributions and Zipf’s law[J]. Contemporary Physics, 2005，46(5)：323-351.