一阶线性时滞系统的内模控制设计

罗霄华

(太原理工大学信息工程学院，山西太原 030024)

0 引言

1982年，Garcia C E和Morari M提出具有模型、控制、反馈环节的内模控制(internal mode contro1)，由于具有良好的跟踪性能和抗外扰能力，并对模型不确定性有一定的鲁棒性，内模控制自面世以来，不仅在工业过程控制中获得了成功应用，而且在控制系统稳定性和鲁棒性理论分析方面也具有一定的优势。尤其是多变量内模控制可以直接调试整个闭环系统的动态性能，并对模型误差具有良好的鲁棒性，因此，内模控制也是分析与设计多变量过程控制系统的一种重要方法。在工业过程中，简单的PID控制可以解决绝大部分的控制问题，然而对于强耦合多变量过程、强非线性过程、大惯性过程和时滞过程，常规的PID控制难以得到满意的控制效果。采用内模控制结合PID控制，比单纯采用PID控制器的控制效果好。与经典的PID控制相比，内模控制结合PID控制仅需整定一个参数，参数调整与系统的动态品质和鲁棒性的关系比较明确。

1 内模控制

1.1 原理及其结构图［1］

内模控制(Internal Model Control，简称IMC)是一种基于过程数学模型进行控制器设计的控制策略。由于其设计简单，控制性能好和在系统分析方面的优越性，因而它不仅是一种实用的先进的控制算法，而且还是研究预测控制等基于模型的控制策略的重要理论基础，以及提高常规控制系统设计水平的工具。其结构框图如图1所示。

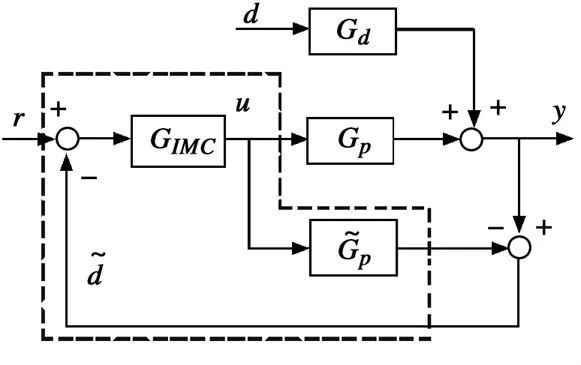
图1 内模控制框图

系统的特征方程为:

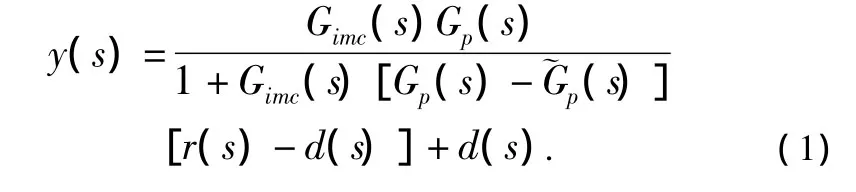
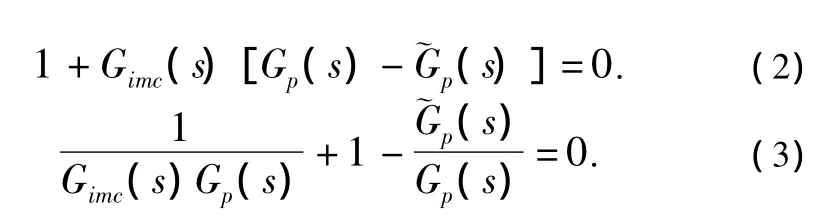
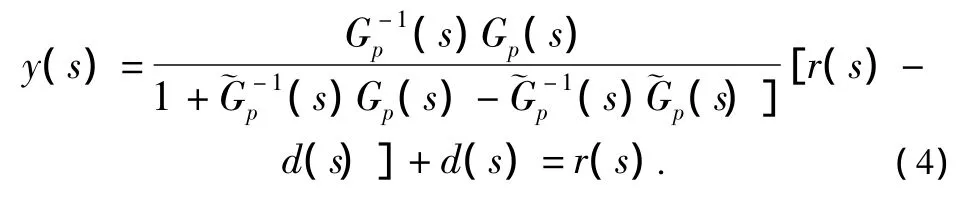
即输出可以完全复现输入。

1.2 基于内模PID鲁棒性控制器的设计［2，3］

若过程Gp(s)稳定，过程模型定义准确，且当Gp(s)=)，模型的逆存在时，则理想控制器的特性为［3］:

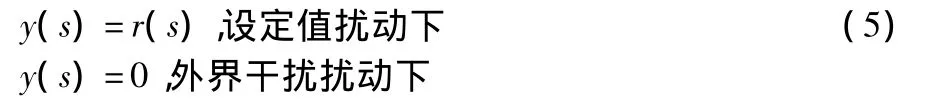
即系统可以克服任何干扰d(s)，实现对参考输入的无偏差跟踪。但理想控制器的特性是在－1p(s)存在且控制器Gimc(s)可以实现的条件下得到的。由于对象中常见的时滞和惯性环节，使－1p(s)中出现纯超前和纯微分环节，因此，理想控制器是很难实现的。此外，对于具有反向特性，即包含不稳定零点的过程，－1p(s)中甚至还含有不稳定极点。另外，由于模型误差，闭环系统的鲁棒性也无法确定。

1.3 控制器的设计过程［4］

1.3.1 理想的 PID控制器

理想的PID控制器具有如下形式:

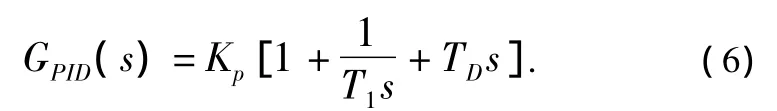
图1虚线框内等价的反馈控制器G(s)和内模控制器Gc(s)之间有如下关系:

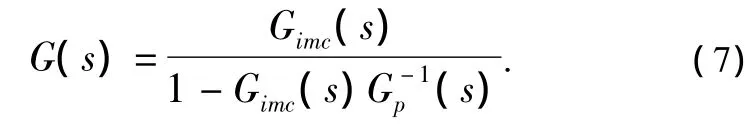
1.3.2 控制器的设计

内模控制器可分为三步进行设计。首先，暂不考虑系统的鲁棒性和约束，设计一个定的理想控制器;其次，引入滤波器，通过调整滤波器的结构和参数来获得期望的动态品质和鲁棒性;最后，对系统的抗干扰性进行验证。

(1)过程模型G(s)的分解

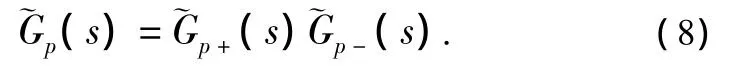
(2)鲁棒性的设计

为了增加鲁棒性，在控制环节中加入一个低通滤波器F(s)。

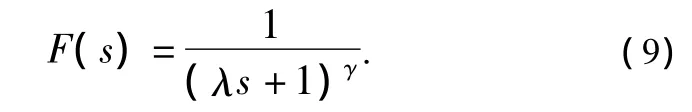
式(9)中:λ是时间常数;γ是使G(s)控制可以实现的阶次。

从图1可以推导出:

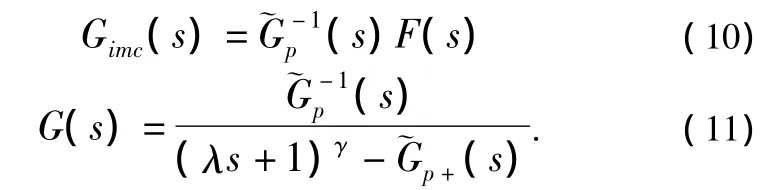
在IMC—PID串级控制中，Gimc(s)和p(s)等都是按照内模控制原理来设计的，与单回路IMC类似，只要满足一定的条件，不管多大的模型失配，F(s)中的参数都能保证闭环系统的稳定。

(3)抗干扰性验证

与单回路控制系统相比较，由于系统在结构上多了一个副回路，所以提高了系统抑制二次干扰的能力。可用信噪比来衡量系统的抗干扰能力。

2 仿真实例

对于典型一阶滞后对象，

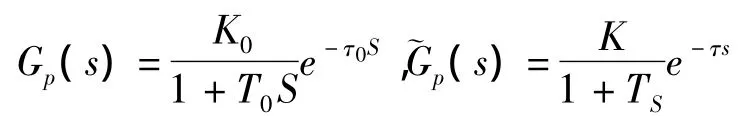
存在建模误差

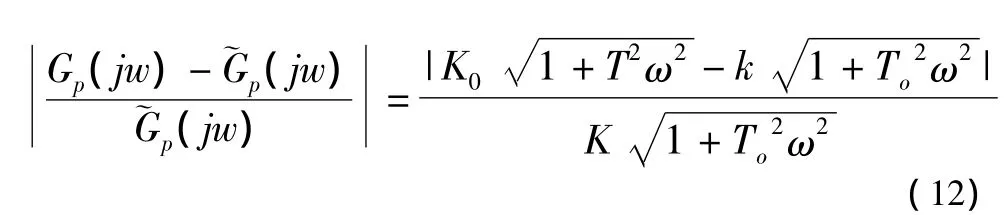
滤波器选为:

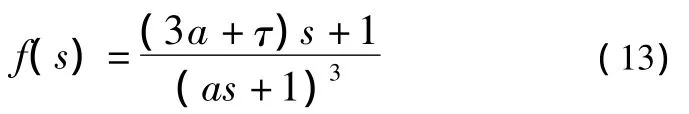
控制器选为

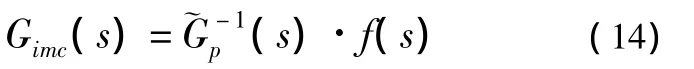
当 Ko=4.56，To=3.21，τ=1.85，K=4.50，T=3.00，τ =2.00时，考虑斜坡扰动，取 a=0.85，可得

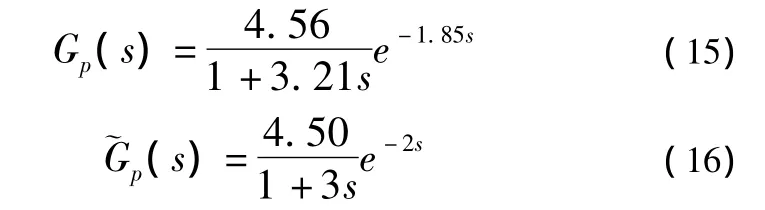
由式(8)－(16)得:

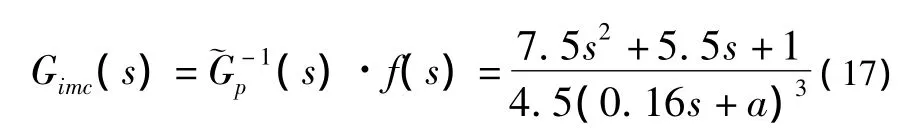
由图1所示结构框图，在SIMULINK环境下，仿真框图如图2所示。

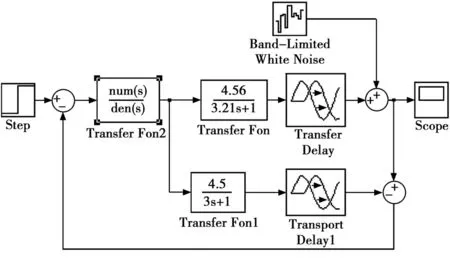
图2 simulink仿真框图

由此框图所仿真出的效果如图3所示。

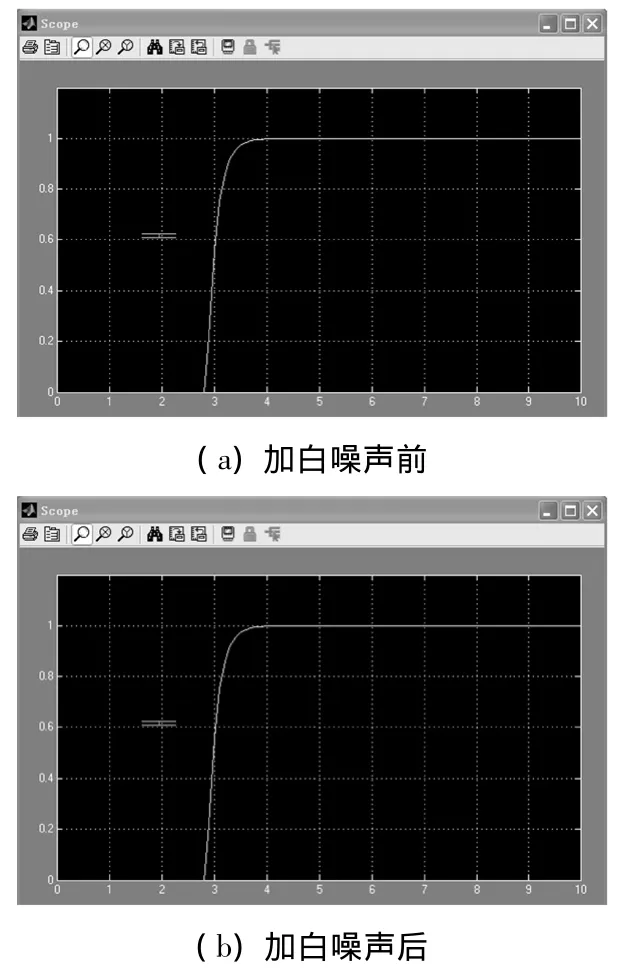
图3 仿真结果

3 仿真结论

由仿真结果图得出IMC系统能无静差地跟踪阶跃信号，此系统的设计有一定的抗干扰能力，并具有较强的鲁棒稳定性能。

［1］王树青.先进控制技术［M］.北京:化学工业出版社，2001.

［2］张小娟.时滞系统的内模控制设计及仿真［J］.新工艺数字技术与机械加工工艺装备，2009(11):29－31.

［3］邵惠鹤.工业过程高级控制［M］.上海:上海交通大学出版社，1997.

［4］高东杰，谭杰，林红权.应用先进控制技术［M］.北京:国防工业出版社，2003.