动态数据驱动的林火蔓延模型模拟误差自适应修正1)

杨广斌 唐小明 李亦秋

(贵州师范大学，贵阳，550001) (中国林业科学研究院资源信息所) (绵阳师范学院)

森林火灾是一个非常复杂的现象，对森林火灾这样复杂系统行为的精确分析和预测是非常困难的。而林火预防和扑救的时效性很强，森林火灾一旦发生，就必须根据影响林火行为的各项因素，确定林火蔓延的趋势，实时有效地预测、模拟林火行为，以便科学、及时地做出林火指挥扑救决策。因此，运用计算机实现林火的蔓延模拟成为必然，这也是当前林火蔓延研究的一个主要方向。尽管先进虚拟现实技术和元胞自动机模型的发展使得现阶段林火模拟在视觉效果和空间扩散方面取得了很大进步，但仍然缺乏对林火蔓延系统的精确描述能力，这种情况在实时动态条件下显得更为突出［1－4］。美国自然科学基金会(NSF)在2000年首先提出了动态数据驱动应用系统(DDDAS，Dynamic Data Driven Application Systems)的研究概念，并推动和资助了多个相关领域的一系列前瞻性研究，其中动态数据驱动的林火蔓延模拟研究项目受到了多个领域专家的推崇［5－7］。

在我国林火模拟研究中，已采用的林火蔓延模型主要有Rothermel模型及王正非的林火蔓延模型［8－9］。林火蔓延模型是建立在一定范围内的模型，都有局限性。对于一个地区的林火蔓延模拟，可以选择适宜的已有林火蔓延模型，再根据本地实际情况对模型进行修正。传统的模型修正方法是通过多次点火试验来确定模型的修正参数。这种模型修正方法不仅周期长、效率低，而且一旦模拟环境有较大变化时，修正的参数就不再适用。文中以动态数据驱动技术为基础，通过对模拟精度验证方法和模拟误差的分析，确定模拟误差修正参数及其计算方法，通过神经网络技术实现模拟误差修正参数自动生成过程，并对模拟误差修正效果进行试验和分析。实现了林火模型的在线自适应修正，从而提高林火蔓延模拟的精确性和时效性。在实践上为林火扑救指挥提供决策支持，在理论上为相关领域的空间扩散模拟研究提供新的思路和技术范式。

1 林火蔓延模拟误差分析

在林火模拟过程中，模拟的林火蔓延与真实的林火蔓延之间只能是最大程度的相近，不可避免地存在模拟的林火蔓延与真实林火蔓延之间的误差问题。

1.1 误差来源

在林火蔓延模拟过程中，误差的来源包括数据误差、模型误差、不同算法和各种测量仪器产生的误差等。

数据误差:包括野外动态气象数据误差、地形数据误差、可燃物数据误差等。

模型误差:林火模型是对实际林火蔓延过程的一种抽象表达，简单的林火蔓延方程不可能把复杂的林火蔓延过程十分准确地表达出来。

算法误差:从动态数据的采集到林火蔓延模拟的实现，涉及许多技术实现的算法，如气象数据插值算法、林火蔓延空间扩散算法等，这些算法会对模拟结果直接或间接地产生影响。

仪器和设备误差:GPS火场位置数据采集、无线传输设备的时间延迟都会对模拟结果造成误差。

1.2 误差表现形式

根据林火模拟结果的表现形式不同，误差主要表现在以下几个方面:

位置误差:实际火场某点位置与模拟火场对应点位置之间的差异，可用距离来表示。如实际火场火头位置点M与模拟火场火头位置点M＇之间的距离l，即是模拟的火头位置M的误差(图1)。

图1 火场位置误差

火线长度误差:实际火线长度与模拟火线长度之差。局部火线长度误差是指实际火场两点之间的长度与模拟火场相应两点之间的火线长度之差(图2中ANB－A＇N＇B＇);整体火线长度误差是指整个实际火场火线总长度与模拟火场火线总长度之差(图2 中ANBM－A＇N＇B＇M＇)。

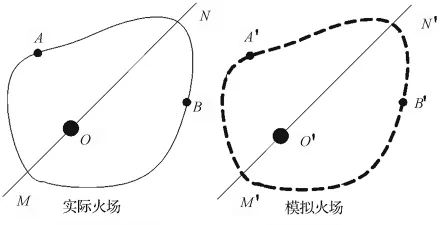
图2 火线长度误差

火场面积误差:实际火场面积与模拟火场面积之差。

火场形状误差:实际火场形状与模拟火场形状之间的差异，可用形状变形系数来表示:

式中:K为变形系数，K值越大，表示形状越规则;A为火场面积;P为火线总长度。

蔓延速度误差:实际林火蔓延速度与模型计算蔓延速度之差。

蔓延方向误差:实际林火蔓延方向与模拟林火蔓延方向之间的差异，可用实际火场某点相对于着火点的方位角与模拟火场对应点相对于着火点的方位角之差来表示，图3中α－β，即为A点的蔓延方向误差。

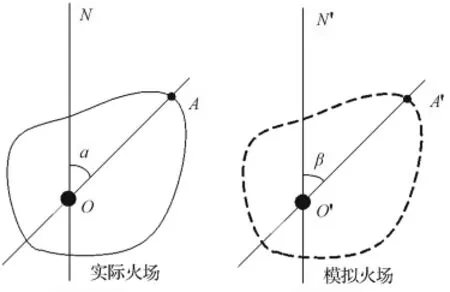
图3 蔓延方向误差

1.3 误差分析

由于林火蔓延的位置、火线长度、火场形状和火场面积直接由林火蔓延的速度和蔓延方向决定，所以，在上述几种误差中，林火蔓延速度误差和蔓延方向误差是最基本的误差，直接决定着其他几种误差的大小。林火蔓延方向主要受风向的影响，在复杂地形条件下，风向受地形的影响比较大，因此，通过地形风场模型可减小林火蔓延方向误差［10－12］。

文中主要探讨如何通过减小蔓延速度误差减小林火蔓延模拟的误差。

林火蔓延速度误差是由多种因素共同影响产生的，通过对模型中的每个影响因子进行修正来减小模拟误差的做法是不现实的。因此，文中通过对模型增加一个全局修正因子，使林火蔓延模拟速度与实际林火蔓延速度相等，从而实现对林火蔓延模拟误差的修正。

2 模拟误差自适应修正

人工神经网络，或称神经网络(Neural Networks，简称NN)是由大量的、同时也是很简单的处理单元(或称神经元)广泛地互相连接而形成的复杂网络系统，它反映了人脑功能的许多基本特性，是一个高度复杂的非线性动力学系统。神经网络具有大规模并行、分布式存储和处理、自组织、自适应和自学习能力，特别适用于处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题［13］。文中基于动态数据驱动技术和神经网络原理构建林火蔓延模拟误差在线自适应修正系统，模拟误差的在线自适应修正就是在动态输入的火场环境数据驱动作用下，通过林火模拟，根据火场环境数据自动地生成模拟误差修正参数值，并在模拟过程根据火场精度验证数据形成学习样本和进行知识积累的过程。这个过程是一个系统自学习、自适应和自动知识积累的过程(图4)。

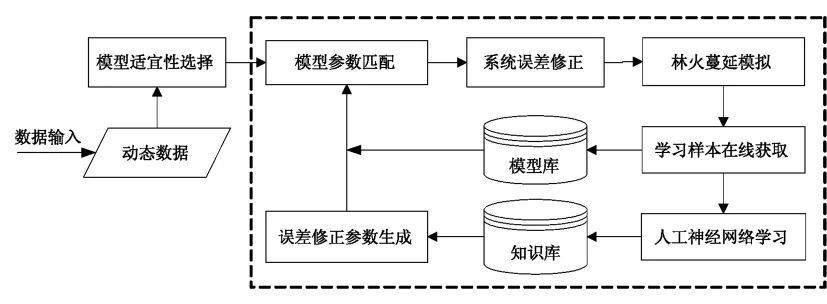
图4 模拟误差在线自适应修正过程

2.1 模拟误差修正参数确定

不同林火蔓延模型，其表达式不同，输入参数和输出结果也不相同，即使同一个模型，当模拟环境条件改变时，其参数也随之改变。林火蔓延模型用一般函数可表示为:

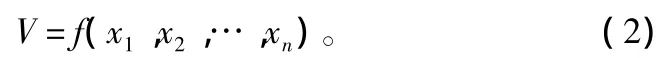
式中:V为林火蔓延模拟速度;x1，x2，…xn为林火蔓延影响因子，如植被、坡度、风力等;n为影响因子个数。

实际林火蔓延速度为R，则R可表示为:

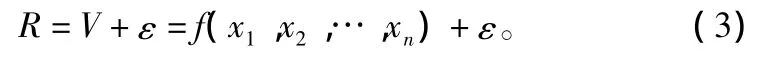
式中，ε为林火蔓延模拟误差修正参数，则有:

设林火蔓延的最大实际速度为Rmax，则ε的最大取值范围为:

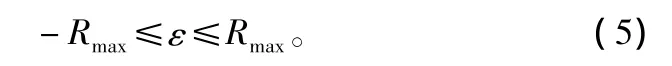
由以上模拟误差修正参数推算公式可知，模拟误差修正参数由实际林火蔓延速度R和林火模型计算速度V之差决定。

林火蔓延的实际速度是通过实时测量方法获取的。火场环境数据是相应火场实时获取的火场环境数据。根据火场环境数据和林火蔓延模型可计算出林火蔓延的理论速度，这样就可以计算出模型的模拟误差修正参数。

2.2 神经网络模型构建

反向传播(BP)网络就是一种多层前向神经网络，是目前最常见、应用最广泛的一种神经网络。从结构上讲，它由输入层、中间层(隐含层)和输出层组成，网络中每个神经元通过求输入权值和经激活函数传递结果来工作，通过改变学习速率、动量因子可以提高BP学习算法的收敛速度［14－15］。文中以王正非模型为基础，构建林火蔓延模拟误差修正神经网络模型。

确定输入输出结点:根据火场环境因子和林火蔓延模型参数，确定输入结点为植被、坡度、风速、气温、大气湿度5个因子，用向量表示为:

X=［植被，坡度，风速，气温，大气湿度］。

输出结点只有1个，即模拟误差修正参数。

确定隐含层结点数:隐含层结点数通过输入层和输出层结点数来确定，即取输入输出层结点数的平均值，因此，隐含层结点数为3。

构建神经网络结构:建立一个3层的BP神经网络，网络结构如图5所示。

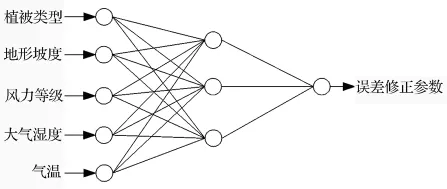
图5 模拟误差修正参数预测神经网络结构

确定作用函数:作用函数为(0，1)S型函数:

学习速率、动量因子和最小期望误差的确定:学习速率决定每一次循环训练中所产生的权值变化量。大的学习速率可能导致系统的不稳定;小的学习速率导致较长的训练时间，可能收敛很慢，但能保证网络的误差值不跳出误差表面的低谷而最终趋于最小误差点。附加动量使权值的修改增大，合适的动量因子可加快学习过程的收敛速度，但是值过大也会引起学习过程的振荡，动量的大小尚无定论，通常由试验确定。

2.3 模拟误差修正参数获取

由历史火场环境数据和火场实际蔓延速度数据，计算生成模拟误差修正参数。系统在正式运行之前无法自动获取模型选择的学习样本，这就需要利用历史火场记录数据作为训练样本来形成模型选择的知识。林火模型本身所带的参数与计算得到的模拟误差修正参数是一一对应的，将其进行匹配(图6)，生成原始学习样本(表1仅列出部分样本)。

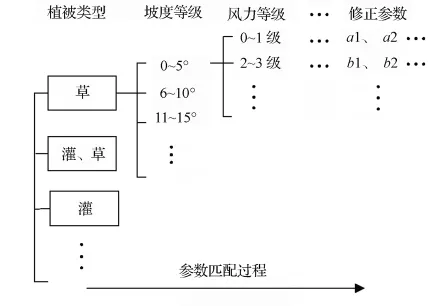
图6 模型参数匹配框架结构及匹配过程

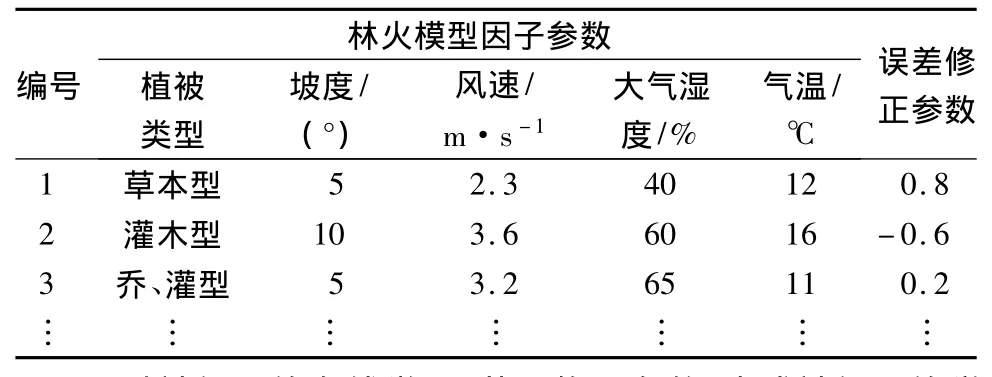
表1 原始学习样本

通过神经网络在线学习，获取修正参数，生成神经网络学习样本。历史数据获取误差修正参数是有限的，需要通过神经网络学习，生成新的学习样本。在火场动态数据的驱动下，网络学习样本是在林火模拟过程中自动产生的，其生成过程如图7所示。

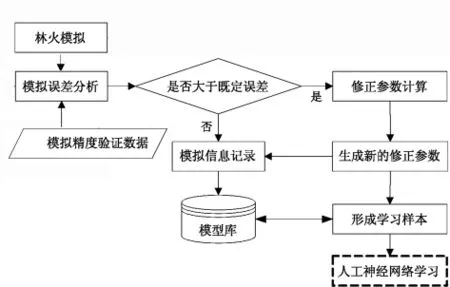
图7 网络学习样本在线获取过程

通过以上2种方式获取到的模拟误差修正参数精度是不同的，从历史数据获取的参数与火场环境是一一对应的关系，也是经过实际测量数据验证的，具有较高的精度，不需要经过再修正。而由神经网络预测自动生成的误差修正参数，它只是一个预测值，或者说是估算值，是经过知识推理产生的，它的精度依赖于神经网络先前学习的样本精度和样本数量，与火场环境数据不具有一一对应关系。因此，在模型模拟误差修正参数匹配时，首先从数据库中搜索是否有与输入的火场环境数据相匹配的误差修正参数，如果有，则直接读取此参数作为这次模拟的误差修正参数;如果没有，则通过神经网络和知识库自动生成一个误差修正参数，用此参数作为模拟的修正参数，如果模拟结果误差超出预期值，则还要通过验证数据对此参数进行再修正。

按照上述设计的模拟误差修正过程，模型模拟误差修正参数是一个常数，它是对一场林火过程中的某一时间段内的林火蔓延速度的修正，并假定在这个时间段内火场环境因子数据是单一的、均匀的、不变的。但是，在实际林火燃烧过程中，火场环境因子是不断变化的，模型模拟误差修正参数也是随着环境的变化而改变的。因此，模型模拟误差修正参数是一个可变常数，它是随着火场动态输入的环境因子的数据变化而改变的，火场每输入一次数据，模型模拟误差修正参数就会相应地改变1次。这种模拟误差的修正即为动态数据驱动的林火蔓延模拟自适应修正。

3 模拟误差修正试验

3.1 试验数据

为了验证模型修正方法的有效性，文中采用历史记录火场数据进行试验。在1986—2010年北京市历史火场中，选择出适宜于王正非模型模拟的96条记录，作为模拟误差修正参数自动生成的试验样本集，其中80条记录作为学习样本，16条记录作为验证样本。选择火场记录的原则是:保证比较单一的火场环境，即植被、坡度、风速、气温、大气湿度这些因子值在同一场林火中变化较小;过火面积不宜过大，避免实际火场环境比较复杂，使计算出的林火蔓延速度与实际蔓延速度相差较大。表2为选取的历史火场记录。

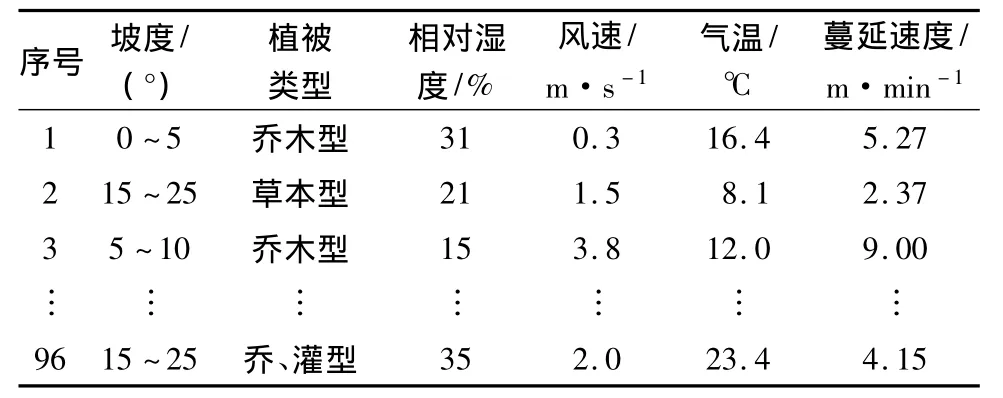
表2 模型模拟的火场数据记录

3.2 数据标准化处理

由火场采集的数据不能直接作为神经网络的输入数据，需要对数据进行标准化处理。在进行神经网络计算时，为了加快网络的收敛速度，将数值一般采用［0，1］表示的形式，即对数值进行极值标准化计算。数据标准化处理步骤如下:

对原始数据进行分类或分级，并采用数值形式表示。

坡度分级数值化为:1表示坡度为0°～5°;2表示5°～10°;3表示10°～15°;4 表示15°～25°;5 表示25°以上的坡度。

植被分类数值化为:1表示草本型植被;2表示灌草型植被;3表示灌木型植被;4表示乔灌型植被;5表示乔木型植被。

求平均值。用u1k，u2k，…，uik，…，unk，uik表示第i个样本对第k项指标取得的数据，i=1，2，…，n，n=12，k=1，2，3，4，5。原始数据平均值:

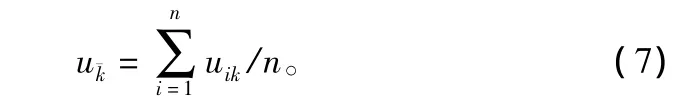
求标准差。原始数据标准差:

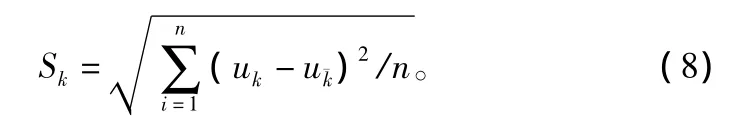
求标准化值。原始数据标准化值:

数据极值标准化。采用极值标准化公式计算，得到［0，1］区间的标准化数据:

式中:u＇maxk和u＇mink分别表示u＇1k，u＇2k，…，u＇nk中的最大值与最小值。

神经网络的输出样本是根据模拟误差修正参数计算公式求得的。首先根据火场环境因子、过火面积和着火时间计算出林火蔓延的实际速度，然后把火场环境因子输入王正非模型中计算出模拟速度，最后求得模型蔓延速度的误差修正值，此修正值本身是数值型，不需要再进行模式转换，可直接作为神经网络的输出因子值。

3.3 试验结果

在试验中，BP网络的学习速率η=0.3。采用附加动量的权值修正，权值调节的动量因子取α=0.75。网络实际输出和目标输出的最小期望均方误差定为0.01。当神经网络训练次数达到650次时，网络满足了预先设定的精度要求。试验结果形成的网络权值和阈值为:

式中:W1表示网络权值矩阵;W2表示网络权值转置矩阵:B1表示网络阈值矩阵:B2表示网络阈值的转置矩阵。

3.4 修正效果分析

为了验证以上网络学习的效果，将整理好的16场历史火场记录作为网络输入因子，预测其输出值。将神经网络生成的修正参数与计算得出的修正参数进行对比，评估神经网络的预测精度(表3)。

在以上预测的16条记录中，其中14条与计算结果误差小于预定的 0.20 m·min－1，2 条误差超过0.20 m·min－1，因此，通过试验可知，模拟误差修正结果精度具有一定的可靠性。

4 结论与讨论

林火蔓延速度误差和蔓延方向误差是最基本的误差，直接决定着其他几种误差的大小。地形风场模型可减小林火蔓延方向误差，文中主要探讨通过减小蔓延速度误差减小林火蔓延模拟的误差。

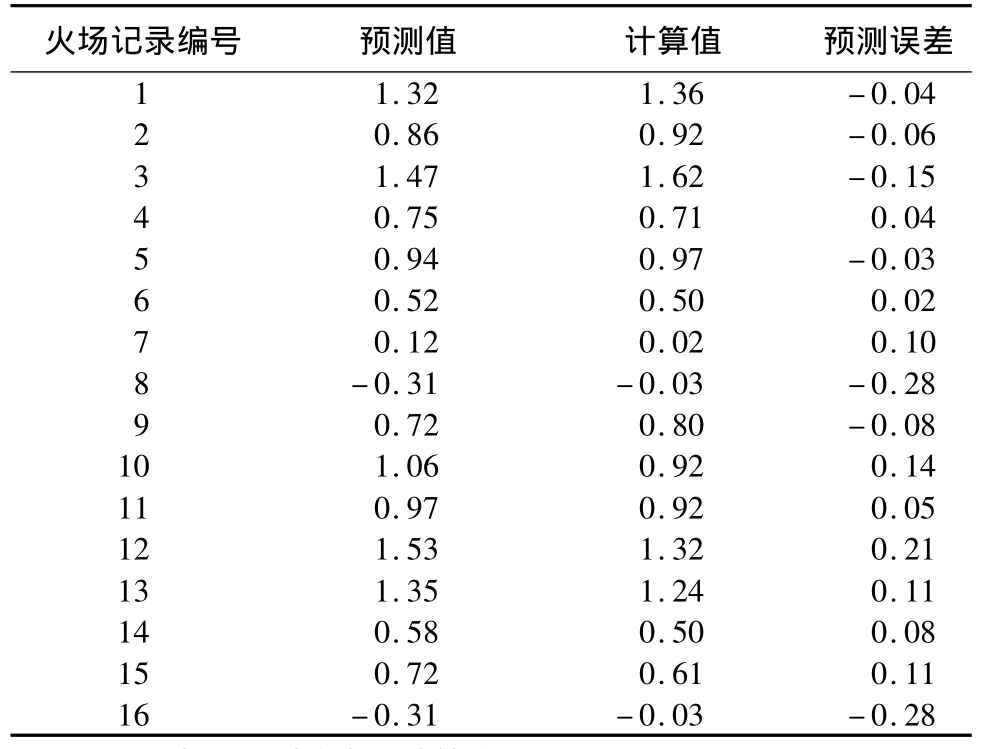
表3 预测值与计算值结果对比 m·min－1

确定了模拟误差修正参数的计算方法，基于动态数据驱动技术和神经网络技术构建林火蔓延模拟误差在线自适应修正系统，探讨模拟误差在线自适应修正机制和模拟误差修正知识在线自动获取机制，实现模拟误差的在线自适应修正过程。

以王正非林火蔓延模型为例，采用历史记录火场数据对模拟误差的自适应修正过程进行了试验。选择了96条记录作为试验样本集，其中80条记录作为学习样本，16条记录作为验证样本。在预测的16条记录中，其中14条与计算结果误差小于预定的 0.20 m·min－1，2条误差超过 0.20 m·min－1，模型模拟误差修正达到了较为理想的效果。

基于动态数据驱动和神经网络技术构建的林火蔓延模拟误差在线自适应修正系统，提供了火场环境数据和林火蔓延速度数据采集机制，是一个自学习、自适应和自动知识积累的系统，随着系统的不断完善和数据、知识的不断积累，将最终解决林火蔓延模拟数据瓶颈问题，实现林火蔓延模拟与真实的林火蔓延之间最大程度的相近。

［1］田勇臣，刘少刚，赵刚，等.森林火灾蔓延多模型预测系统研究［J］.北京林业大学学报，2007，29(4):49 －53.

［2］McDonough J M，Yang T.Parallel performance of a new model for wildland fire spread predictions，paralle CFD(Computational Fluid Dynamics)Conference［J］.Las Palmas de Gran Canaria(ES)，2004(5):45－51.

［3］Trunfio G A.Predicting wildfire spreading through a hexagonal cellular automata model［J］.Lecture Notes in Computer Science，2004，33(5):385 －394.

［4］黄华国，张晓丽，王蕾.基于三维曲面元胞自动机模型的林火蔓延模拟［J］.北京林业大学学报，2005，27(3):94 －98.

［5］Ouyang Ying，Zhang Jiaen，Luo Shiming.Dynamic data driven application system:Recent development and future perspective［J］.Ecological Modelling，2007，204(1/2):1 －8.

［6］Pidd M.Guidelines for the design of data driven generic simulators for specific domains［J］.Simulation，1992，59(4):237 －243.

［7］Mosterman P J，Sztipanovits J，Engell S.Computer－automated multiparadigm modeling in control systems technology［J］.IEEE Transactions on Control Systems Technology，2004，12(2):223 －234.

［8］唐晓燕，孟宪宇，易浩若.林火蔓延模型及蔓延模拟的研究进展［J］.北京林业大学学报，2002，24(1):87 －91.

［9］Richards G D.A general mathematical framework for modeling twodimensional wildland fire spread［J］.International Journal of Wildland Fire，1995，5(2):63 －72.

［10］Feliks Y，Gavze E，Givati R.Optional vector interpolation of wind fields［J］.Journal of Applied Meteorology，1996，35:1153 －1158.

［11］桑建国，温市耕.大气扩散的数值计算［M］.北京:气象出版社，1992:35－38.

［12］余琦，刘原中.复杂地形上的风场内插方法［J］.辐射防护，2001，21(4):213 －218.

［13］田晓瑞，舒立福，王明玉，等.西藏森林火灾时空分布规律研究［J］.火灾科学，2007，16(1):10 －14.

［14］侯彦东，方惠敏，杨国胜，等.一种改进的可变学习速率的BP神经网络算法［J］.河南大学学报:自然科学版，2008，38(3):301－312.

［15］张会生，吴微.一种具有自适应动量因子的BP算法［J］.大连海事大学学报，2008，34(4):45 －51.