基于Pushover方法的钢框架结构超强分析

李 东，苏恒品

(1.东北电力大学建筑工程学院，吉林吉林132012;2.国电东北新能源发展有限公司，辽宁沈阳110027)

历次地震反映出大震作用下结构所遭受的地震作用虽然远大于设计地震力［1-4］，但结构并未倒塌，甚至未出现严重的损坏。结构通过变形耗散大量地震输入能量的同时，结构超强也起到了重要作用。结构超强定义为在地震作用下结构的实际反映性态所确定的当量屈服强度与结构设计强度的比值。结构的超强主要与以下因素相关:①材料的超强;②截面的正公差;③设计人员构件截面选择所带来的人为超强;④结构赘余度引起的超强;⑤荷载的分项系数所引起的结构超强;⑥非结构构件引起的结构超强等。目前，精确预计结构的超强仍存在很大困难，一些国家的抗震规范(美国IBC2003、加拿大NBCC2005、欧盟EC8等)主要依据工程经验初步确定了不同结构体系的超强系数，而我国的抗震规范尚未合理考虑结构超强的影响［4-6］。虽然国内一些学者对结构超强也展开了研究［7-11］，但成果还有待进一步研究。

为了进一步量化我国规范所设计结构的实际超强能力，本文严格按中国规范设计了6榀钢框架结构，考虑了设防烈度、层数、加载模式等因素的影响，基于静力弹塑性分析给出了钢框架结构体系的超强系数，并进一步分析了结构缀余度超强。

1 结构超强系数的确定

结构的超强系数可按公式(1)计算:

式中，Vu为结构实际水平极限剪力;Vd为结构设计剪力标准值。

由于结构超强的影响因素很多，因此，结构超强系数RΩ还可表达为公式(2)。

式中，R1为材料屈服强度的超强;R2为水平地震作用荷载分项系数的超强;R3为结构体系的缀余度超强;R4为其它超强，包含设计人员选择截面导致的人为超强、竖向荷载起控制作用等导致的超强等。

参考美国相关规范及我国相关钢材的材性试验，材料屈服强度的超强系数R1取1.3。水平地震作用荷载分项系数的超强系数R2取 1.3［4，6］。

2 结构模型、非线性模拟及分析计算

2.1 结构模型

采用中国建筑科学研究院开发的有限元分析设计软件STS，严格按我国相关规范设计了6榀刚接钢框架。算例层数分别为5层、10层及15层，跨度为7.2米，层高均为3.6米，柱距为7.8米。钢材等级为Q235B。楼面恒(活)4.7(2.0)kN/m2，屋面恒(活)5.0(2.0)kN/m2。设防烈度分别为 8 度(0.2 g)、9 度(0.4 g)，地震分组为第一组，二类场地。结构平面布置见图1，结构立面见图2，设计结果见表1。

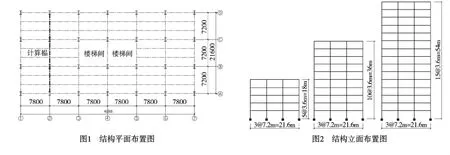
表1 钢框架梁柱截面

2.2 非线性模拟

钢框架结构采用平面杆系模型，结构分析采用SAP2000非线性有限元程序。材料非线性采用集中塑性铰模拟，框架梁采用M弯曲铰模拟，框架柱采用耦合的PM轴力-弯曲铰模拟。同时也考虑结构的几何非线性。

2.3 分析计算

首先通过振型分解反应谱方法确定了本文6个平面钢框架结构的基底剪力标准值Vd，随后通过Pushover方法确定了结构首次出现塑性铰时结构的基底剪力Vh1，并获得结构的能力曲线。结构的水平极限基底剪力Vu取结构最大层间侧移达到2%时所对应的基底剪力。

Pushover方法采用了均匀分布、倒三角分布及广义乘方分布三种固定的水平荷载分布模式。表2、表3计算出8度区、9度区三种水平荷载分布模式下的Vd、Vh1、Vu值。

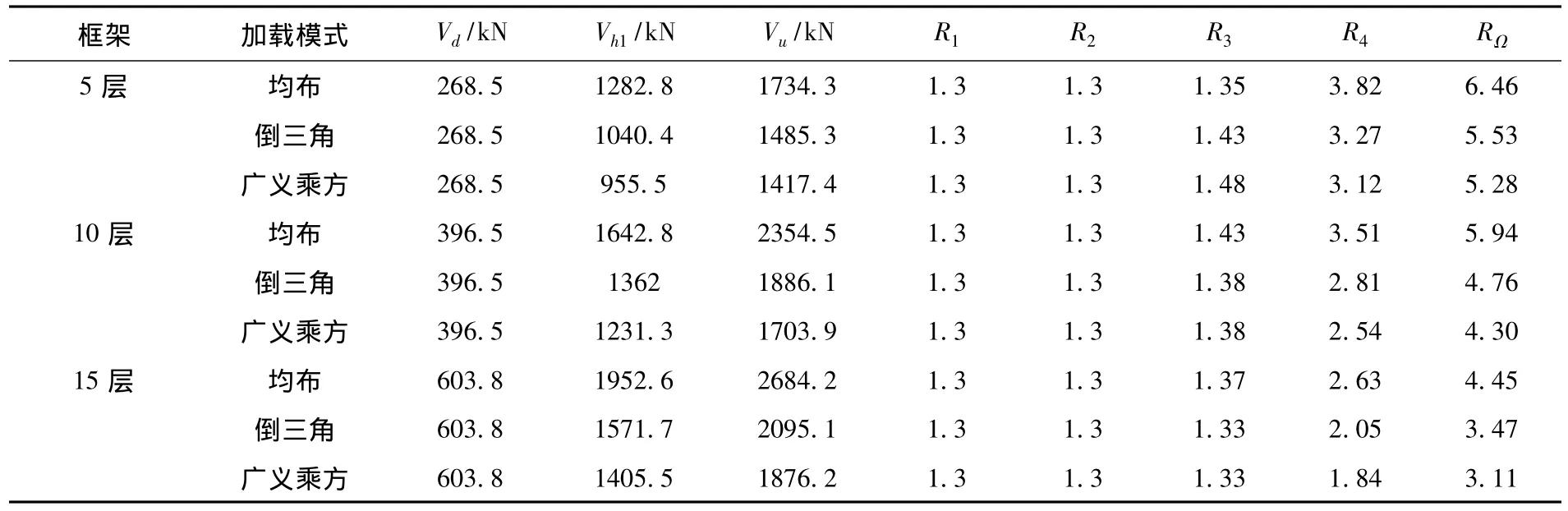
表2 8度区钢框架结构超强系数

表3 9度区钢框架结构超强系数

3 结构的整体能力曲线

多自由度体系属于高次超静定结构，具有多种屈服机制。结构的抗侧能力由结构的屈服机构决定，这也意味着与外荷载相关。因此，为了更合理地评价钢框架结构的整体抗侧能力，本文选用了三种具有代表意义的水平荷载分布模式。

图3～图4给出了8度区、9度区钢框架结构在三种水平荷载分布模式作用下的能力曲线。

从图3～图4可知:

(1)三种水平荷载分布模式作用下获得钢框架结构的能力曲线存在明显差异，其中，未考虑高阶振型影响的均匀分布模式下所获得的结构能力曲线最高，等效抗侧刚度最大，结构整体变形能力最低。倒三角分布模式同广义乘方分布模式所获得的钢框架能力曲线差异较小，广义乘方分布模式部分考虑了高阶振型影响，获得结构的承载能力最低，等效抗侧刚度最小，但结构整体变形能力最大。

(2)均匀分布模式所获得结构的整体屈服位移小于倒三角分布及广义乘方分布模式所获得的屈服位移。

由此可见，加载模式对结构首次屈服剪力及极限剪力均有显著影响。

4 结构超强的影响因素分析

4.1 设防烈度的影响

为了更合理地评价设防烈度对钢框架结构缀余度超强系数以及结构体系超强系数的影响规律，以考虑高阶振型影响的广义乘方分布为例，本文归纳了设防烈度对R3、RΩ影响规律，分析结果见图5。

图5 不同设防烈度下钢框架的超强系数

由图5可知，设防烈度对结构的缀余度超强影响不大，但对结构体系的总体超强影响较大，随着烈度的增加，结构超强呈增大趋势。

4.2 层数和加载模式的影响

结构缀余度超强R3、结构体系超强RΩ随结构层数及加载模式的变化规律，见图6-图7。

图6 8度设防烈度下钢框架的超强系数

从图6～图7可知，加载方式、结构层数对结构缀余度超强影响不大。随着结构层数的增加，结构的超强系数R呈降低趋势。均匀分布模式下pushover分析获得结构的超强系数R最大，广义乘方分布模式下pushover分析获得的结构超强系数R最小。

图7 9度设防烈度下钢框架的超强系数

5 结 论

通过对6榀钢框架的Pushover分析获得了结构超强的变化规律，总结出如下结论:

(1)水平荷载分布模式对刚接钢框架结构的超强系数影响较大。均匀分布模式下结构的超强系数最大，广义乘方分布模式下结构的超强系数最小。9度区15层钢框架结构均匀分布模式结构的超强系数为4.14，而广义乘方分布模式下结构超强系数为2.86。为合理确定结构的超强能力，应考虑结构高阶振型的影响。

(2)随着设防烈度的提高结构超强系数呈降低趋势。

(3)结构层数对结构超强系数有较大影响。随着结构层数增加，结构的超强系数呈降低趋势。

［1］MARANDA E.Site - dependent strength reduction factors［J］.Journal of Structural Engineering.1993，119(12):3503 - 3519.

［2］KAPPOSA J.Evaluation of behavior factors on the basis of ductility and overstrength Studies［J］.Engineering Structures.1999，21(9):823-835.

［3］BORZI B，ELNASHA I A S.Refined force reduction factors for seismic design［J］.Engineering Structures.2000，22(10):1244 - 1260.

［4］韦锋，李刚强，白绍良.各国设计规范对基准设防地震和结构超强的考虑［J］.重庆大学学报，2007，30(6):102-120.

［5］翟长海，谢礼立.结构抗震设计中的强度折减系数研究进展［J］.哈尔滨工业大学学报，2007，39(8):1177-1183.

［6］童根树，赵永峰.中日欧美抗震规范结构影响系数的构成及其对塑性变形需求的影响［J］.建筑钢结构进展，2008，10(5):52-63.

［7］周靖，蔡健，方小丹.钢筋混凝土框架结构抗震超强系数分析［J］.世界地震工程，2007，23(4):227-233.

［8］翟长海，谢礼立.钢筋混凝土框架结构超强研究［J］.建筑结构学报，2007，28(11):101-106.

［9］刘文渊，何若全，冷捷.单层钢框架结构影响系数分析［J］.苏州科技学院学报，2010，23(2):32-36.

［10］周靖，蔡健，方小丹.剪切型结构的抗震强度折减系数研究［J］.地震工程与工程振动，2008，28(2):64-71.

［11］周靖，赵卫锋.建筑抗震设计地震作用折减系数的取值方法［J］.防灾减灾工程学报，2007，27(4):465-469.