基于相关处理的OFDM信号循环前缀盲估计方法
汤新广
(中国电子科技集团公司第五十四研究所,河北石家庄050081)
0 引言
OFDM系统中为解决因多径信道而产生的ISI问题,在有效符号周期前面加保护间隔。保护间隔的类型包括3类:保护间隔全部置零ZP(Zero Padding)、CP和既置入零又置入循环前缀(ZC)。在OFDM监测系统中,保护间隔特征中最难识别的恰恰是最常用的CP类型。这里提出了一种基于CP循环相关的保护间隔参数估计方法,该方法充分利用了OFDM信号的时域准周期性,以估计出的符号速率等参数作为输入条件,采取窗口滑动相关的方法,实现了FFT时间长度、保护间隔周期和符号同步时刻等参数的精确盲估计。
1 循环平稳特性分析
OFDM具有循环平稳特性,其循环周期是一个OFDM符号周期T。但与单载波系统不同的是,由于OFDM信号在发送端进行了串并转换,并加入了循环前缀CP,所以T=PTe,因此,OFDM信号是在一个符号周期内具有较强的相关特性,但多个符号周期时则不具备完全的循环平稳特性。
参见文献[3],当Q=1时,可求得OFDM信号的周期自相关函数为:
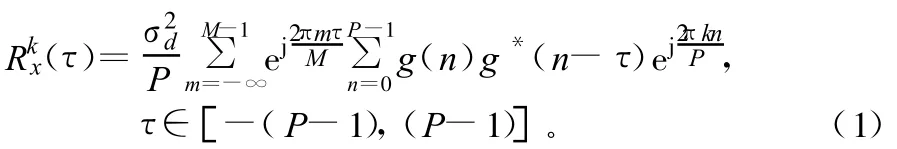
为进一步分析利用周期自相关特性能够获得的信号处理增益Gs,设Lp为CP长度为相对于OFDM符号速率1/T的点数,p为CP符号同步时的起始点,NFFT为有效符号周期点数,当取信号长度m≤Lp,相关的时间间隔为NFFT,则式(1)可简化为:
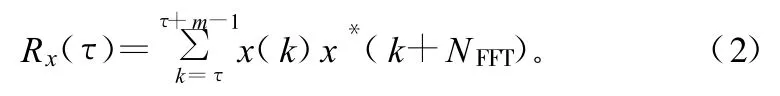
则
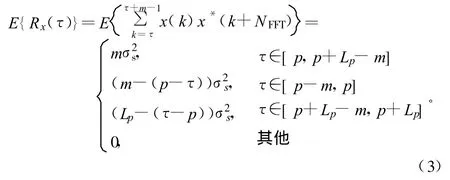
由此可以分析出一个OFDM符号周期T内,当取信号长度m=Lp时,周期自相关函数的最大值为,因此,利用周期自相关特性可获得的最大处理增益为Lp。但为了获得这样的处理增益,就必须保证符号定时同步的前提条件。
利用信号周期谱处理,实际上就是利用信号在α=0和 α≠0时的谱信息,即充分利用了OFDM信号的CP信息。周期平稳信号经过时不变信道后,接收信号仍然是周期平稳的,而经过时变信道的信号不再具有严格意义上的周期平稳性。但在信道相干时间内信道的变化很小时,接收信号仍可近似为周期平稳的。因此,利用OFDM信号周期平稳特性可以实现信号的循环前缀周期的精确估计、系统时延和频偏等同步参数盲估计。
2 CP检测方法
在OFDM侦察接收系统中,仅知道符号周期参数是无法完成准确的符号定时同步。帧检测有2个任务:分组检测和符号定时。分组检测的目的是确定数据分组的开始时间,而判决数据分组起始沿的最简单方法就是检测接收信号的能量。这里重点研究符号定时的同步点搜索方法。
符号定时是指确定每个OFDM符号开始和结束的精确时刻。符号定时的结果将决定离散傅里叶变换DFT的窗口,也就是用于计算每一个接收OFDM符号的一组取样值;然后DFT的结果用于符号子载波的检波,如图1所示,由于系统并未确定OFDM符号的起始位置,则截取连续2Tc个采样点,其中必包含一个完整的OFDM符号。一个符号周期内前后2个CP数据具有很强的相关性,而其他数据之间不具有相关性。所以利用此特性采用滑动窗时域相关的方法,搜索出符号定时同步点,并估计出有效符号宽度(即FFT周期长度TFFT)。
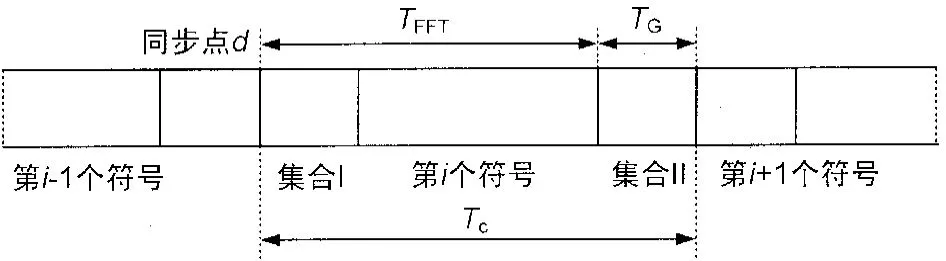
图1 带有循环前缀的OFDM信号结构
如图1所示,定义2个集合:
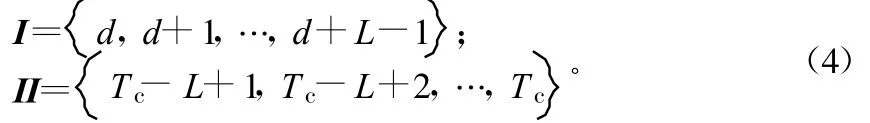
式中,集合 II是OFDM符号的后L个样值,集合 II中的元素复制后放到OFDM符号最前端形成集合I,也就是第i个OFDM符号的循环前缀(CP)。将这2Tc个采样点作为一个向量γ,
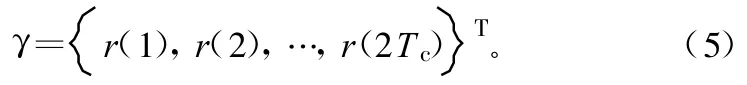
由于集合I与集合II中的元素完全相同,对于r(n)有如下关系:
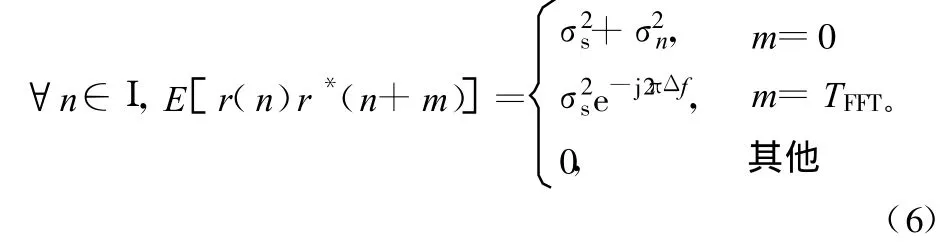
①接收端根据OFDM信号的带宽已完成对信号的时域过采样,得到中频信号s(k);
②根据估计的符号周期Tc对s(k)进行截取,取长度为2Tc的数据g(k)。选取滑动窗长N=,逐段计算窗内的信号gN(k)与g(k)的相关函数c(k)。当进入滑动窗的数据恰是CP时,相关函数就会出现2个峰值,由此可以检测到符号定时的同步点,同时,通过计算CP相关峰值之间的距离得到FFT长度;
③为进一步提高信噪比,若根据估计的符号周期Tc对s(k)进行分段,由于截取时跨2个符号的概率很大,所以为保证一个完整的符号周期仍以2Tc进行选取。计算每段数据的滑动窗与整个数据段的相关函数值Ci(k),并通过采取多段平滑的方法提高信噪比;
④精确估计OFDM信号的多个时域特征参数:FFT长度估计、符号位定时的起始时刻及CP宽度估计。
3 试验仿真与性能分析
3.1 时域平滑对信噪比的改善程度
保护间隔的准确估计有赖于对接收的OFDM信号信噪比的估计性能,所以在保护间隔估计之前需要通过时域平滑提高接收信号的信噪比。通过截取M段的分段数据对应M个OFDM符号,对Yi(k)进行时域平滑得到¯Ci(k)的最大值MAXi。由于AWGN中信号与噪声不相关,则Yi(k)和RC的信噪比分别用SNRY和SNRR表示:
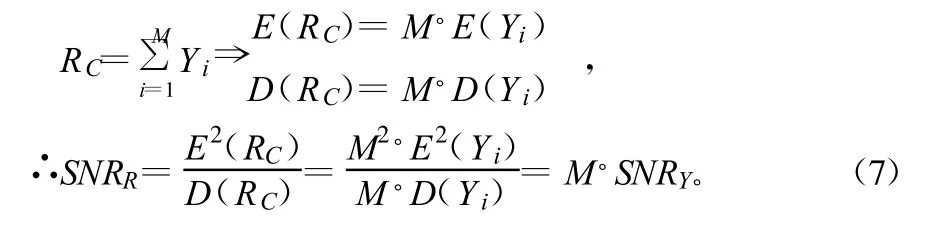
由式(7)可见,经过M次时域平滑,使得信号功率提高了M2倍,而RC中噪声功率为Yi(k)中噪声功率的M倍,这表明理论上信噪比可以改善10log dB。
3.2 试验仿真与结果分析
试验一:归一化采样频率下,fc=0.25,OFDM信号的子载波数为N=128,FFT为512点,CP长度为64,符号周期Tc=576,每个子信道均是QPSK调制。
试验条件:输入信噪比SNR=0 dB,随机选取的符号同步点为DOTsyn=100,以Tc为输入条件,滑动窗长选择为NW=60,平滑次数为100次,计算不同起始点时的平滑相关函数¯Ci(k)的第二峰值Csei。表1给出符号同步点附近第二峰值Csei对应的能量,由表1可见Csei最大能量值对应的位置正是612。
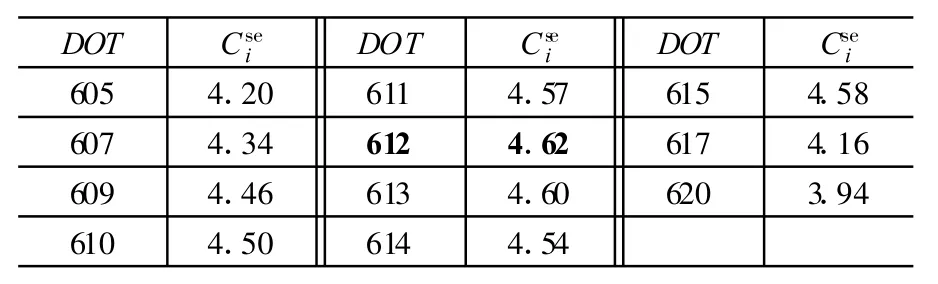
表1 符号同步点搜索试验数据
试验二:图2摘自文献[1]中对CP的估算结果,当其仅利用一个符号周期内的相关函数无法实现CP的有效搜索时,文献[1]也曾想到用将多个符号周期的相关函数累加进行CP估计,但其必须在完成准确同步后才能实现,且仅局限于每个符号周期内进行自相关计算,所以能够获得的CP相关增益并不高。
在与文献[1]中设置完全相同的试验条件下,图3给出了采用该方法平均相关函数平滑10次后的检测结果,通过对比可见,新方法的信噪比改善程度明显优于文献[1]中的方法,且可以准确地估计出信号的同步时刻、CP长度等时域特征参数。这是由于该算法在对分段数据进行时域平滑时选择了2个符号周期的长度,一方面避免了准确同步的前提限制,同时,CP信号与不同时刻的数据随机调制的非CP信号相关性较弱,且与随机噪声或干扰互不相关。滑动互相关比自相关函数更能充分利用了这一差异,所以新方法更能有效增强CP的相关增益,改善信噪比、抑制高斯噪声和干扰。
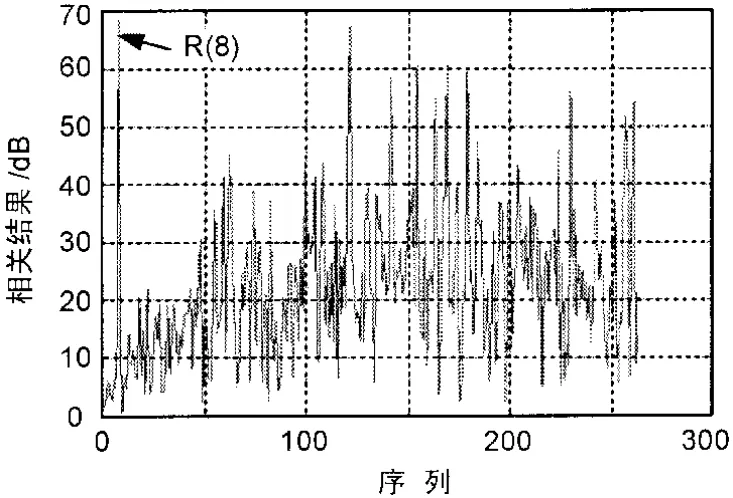
图2 文献[1]图5中的CP估计结果
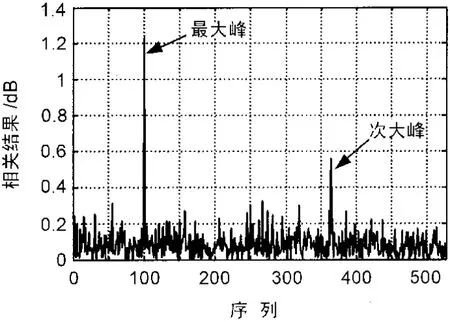
图3 新方法对应文献[1]条件下的检测结果
4 结束语
上述提出的基于循环相关的CP参数估计方法充分利用了OFDM信号的时域准周期性,在符号速率等参数估计的基础上,采取窗口滑动相关实现了对FFT时间长度、保护间隔周期和符号同步时刻等参数的精确盲估计,该方法无需任何先验信息,运算量小、精度高,适于硬件实现,对OFDM信号参数估计具有重要意义。
[1]HONG Li,YEHESKEL B N,ALIABDI,et al.OFDM Modulation Classification and Parameters Extraction[C].2006 1st International Conference on Cognitive Radio Oriented WirelessNetworks and Communications,2006:1-6.
[2]PAR KB,KO E,CHEONH,etal.ABlind OFDM Synchronization Algorithm Based on Cyclic Correlation[C].2001 Global Telecommunications Conference,San,Antonio,Texas,USA,2001:3116-3119.
[3]TANDA M.Blind Symbol-Timing and Frequency-Offset Estimation in OFD M Systems with Real Data Symbols[J].IEEE Transactions on Communications,2004:1609-1612.

