基于曲线内插理论的水库特性曲线计算

李文华，袁中军，谢 强

（临沂市岸堤水库管理处，山东 蒙阴 276217）

水库特性曲线是水库的重要技术指标，是水库规划设计和实际管理工作的重要依据。曲线的计算目前还一直是沿用直线内插的办法进行。这种直线内插近似计算办法优点是计算简便，但结果精度低，往往不能满足工程设计和管理工作的实际要求，目前也没有很好的曲线内插方面的研究和探讨，更没有这方面的解决方案。为此，通过对曲线内插方案的深入探讨和研究，得出了该曲线内插理论。曲线内插理论的核心，就是利用指数方程的曲线组合，平滑连接已知非连续特征点，实现非连续点间的曲线内插，获得非连续点间最符合实际的、优于直线内插的数据，为工程设计和管理，提供可靠的理论依据和计算方法。

现结合临沂市岸堤水库水位库容关系曲线，就怎么用曲线内插理论，取代直线内插办法，用平滑曲线连接非连续点数据这一技术课题，结合矩阵对曲线内插理论进行深入的探讨和研究。

1 曲线内插的基本原理

1.1 建立数学模型

1）理论分析。形如y=axk+b指数方程曲线，其形式是平滑连续曲线。只要合理的确定其参数a、k、b的数据，即可用该曲线，取代原非连续点之间的直线内插为曲线内插，真正寻找到最合理、最符合实际的中间过渡数据。

当然，单单依靠这三个参数a、k、b，实现用指数方程曲线，完全模拟现实生活中的不规则曲线是不现实的，故此，建立如下数学模型。

其中，a、k分别代表系数系列和指数系列。y代表纵坐标，x代表横坐标（下同）。解析该数学模型的关键，是合理的确立指数系列和系数系列数据。

2）指数系列数据的确定。为了用指数方程模拟现实中的不规则曲线，用3个局部特征点数据，通过下列方程组，求解指数系列中的1个指数数据。

建立方程组如下：

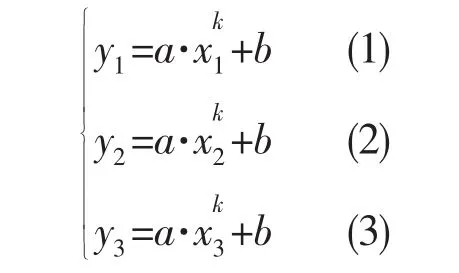
通过化简方程组，即可试算求解出指数k值。

确定指数系列。从已知特征点数据，每次取出3个特征数据，确立一个指数数据。通过选取多组特征点数据，即可分别求出相应的指数系列。

系数系列数据的确定。指数系列数据确定后，可根据特征点数据，建立如下矩阵，求解出系数系列数据a。由以下简化矩阵得到相应的系数系列数据：

2 曲线内插理论的应用

2.1 特征点的确定

首先按照需要内插的位置和已知数据，确定曲线内插方程的定义域，并在该定义域内，选取曲线内插特征点数据。选取更多的特征点坐标，有利于提高曲线内插数据精度，但会极大地增加计算工作量。因此，怎样合理确定特征点，应把握以下两个方面：1）特征点要反映出已知坐标数据的曲线走势；2）要根据数据内插精度要求，合理地确定特征点的数量。既要保证计算精度要求，又要尽量减少不必要的计算工作量。临沂市岸堤水库水位库容关系如图1所示。

假如要计算库水位为172.50时的库容。如图1，选定4个特征点数据（已用圆圈标注，实际应用时，如果对计算精度要求较高，可考虑选取6个或更多个特征点），其相应坐标数据分别为：（171.00，23482）、（172.00，27406）、（173.00，31696）、（174.00，36380），并定义内插方程的定义域为171.00 m～174.00 m。为改善数学模型的参数结构，纵坐标右偏移170个单位。

图1 岸堤水库水位库容关系图

2.2 确定指数系列数据

第一步选取特征点4个，因此指数系列的个数也是4个。1）由于 库水位＝0时，库容≠0，因此，指数系列数据的指数为0。2）由于某库水位对应的水面面积等于库容相对于库水位关系曲线在该水位下的导数，当库水位＝0时，水面面积≠0，因此，指数系列数据的指数为1。3）其他2个指数系列的数据，则根据前面讲到的指数系列数据的确定方法，采用曲线的局部指数表达式的指数值。

取第一组特征点（171.00，23482）、（172.00，27406）、（173.00，31696）将这些特征点坐标数据，分别代入指数方程y=a·(x-x0)k+b（其中x0是坐标偏移量），利用自定义windows动态库函数（或直接采用试算法），解析方程组得：a＝3134.377、b＝20347.6、k＝1.171，故取指数系列数据中的指数为1.171。

取第二组特征点（172.00，27406）、（173.00，31696）、（174.00，36380）计算过程和坐标偏移均同上，得指数系列数据中的指数为1.259。

通过以上计算和分析，在坐标偏移为170时，指数系列数据为 1.259、1.171、1.0、0， 这些指数数据，反映出了曲线的局部特征。

2.3 确定系数系列及方程

根据前面的内容，依据特征点数据和已求得的指数系列数据，建立相应矩阵，利用自定义windows动态库函数（或其他解析法），求得系数系列数据为：-0.000 141 380 894 796 8，0.000 171 387 660 256 7，3 922.80，19559.19。

2.4 数据计算对比

临沂市岸堤水库水位库容关系，局部范围内，可用如下指数曲线方程表示：

其中：y代表库容（万 m3），x代表库水位（1965 黄河基面），170是坐标偏移常数（指数系列和系数系列数据均依此常数计算得到），函数定义域为171.00～174.00 m。计算数据对比如表1示。

表1 数据对比表

由表1定义域范围内的误差百分比，可确定数据的可用性。

利用数学模型将库水位为172.50 m代入上面推导的数学模型方程，得库容为29 396.86万m3。

3 结论

通过以上对临沂市岸提水库水位库容关系的分析和计算，实现了用曲线内插理论，用平滑的指数曲线，连接非连续特征点，求得已知特征点间的中间过渡数据，为工程管理提供了符合客观实际的合理数据，同时也为水库规划设计中水库特性曲线计算提供了新的方法。