南芬露天矿拦水坝渗流与应力耦合分析

李有臣，董宪伟，蔡嗣经

(1．北京科技大学 土木与环境工程学院，北京 100083；2. 本溪钢铁(集团)有限责任公司， 辽宁 本溪 117000)

引言

拦水坝坝址区的地形条件、水文地质条件一般较为复杂，主要表现为覆盖层较厚且分层较多。为了提高坝体的安全性和稳定性，在拦水坝建设之前，首先要对整个坝区的水渗流情况有较全面地了解。根据坝区的工程地质和水文资料，将各地层的渗透特性进行有效地模拟，分析坝体内部渗流场、应力场的相互影响和相互作用，为改善坝体弱应力区和选择心墙提供依据。

1 拦水坝及坝区水文、工程地质概况

本钢南芬拦水坝为土石坝，坝高32 m，顶宽6 m，边坡比1︰2，最高洪水位28 m，坝体内拟设心墙或其它防渗措施。坝址区为山间U型河谷，原有一小溪流通过，小溪枯水期流量为10 m3/s，洪水期大于500 m3/s。两侧山体坡度20°～ 30°，植被发育。两侧山体为花岗岩，风化层厚度小于5 m。右坝肩为块石混杂砂壤土：松散，块石坚固，一般粒径200～500 mm，最大1 500 mm，无磨圆，无分选；河谷区为漂石-卵石混杂砂砾土：松散，块石坚固有磨圆，无分选，一般粒径200～50 mm，最大1 500 mm，厚度约15 m；左坝肩为块石充填黄色粘土，无架空现象，块石成分、组分同右坝肩。两侧坝肩在勘探深度内(孔深最大15 m)未见稳定地下水水位[1]。拦水坝纵剖面如图1所示。

图1 拦水坝心墙示意图

土石坝坝体内部的受力是由内部的渗流场和应力场相互影响、相互作用的结果。一方面，渗流场的改变引起渗流体积力和渗透压力的改变，使坝体作用的外荷载发生变化，从而改变了坝体应力场的分布；另一方面，应力场的改变引起体积应变的改变，使坝体各部位的孔隙率发生变化，渗透系数随之变化，从而也改变了坝体渗流场的分布。渗流场与应力场相互作用、相互影响会使双场耦合达到某一平衡状态，分别形成渗流场影响下的稳定应力场与应力场影响下的稳定渗流场[2-4]。目前对流固耦合问题的研究主要基于有限元方法。并且大多集中在裂隙岩体渗流场与应力场的耦合分析上，实际水利工程中，碾压混凝土坝、土石坝等坝体渗流与应力也存在着较强的耦合作用[5-8]。

2 工程分析

2.1 加载及边界条件

1)土坝中设计心墙的渗透系数远远低于周围土体的渗透系数，认为是不透水材料；

2)水载荷作为静止载荷适用于拦水坝体，最高水位为28 m；

3)计算时重点考虑最高水位的载荷；

4)坝体底部侧边界为零流量边界，且在计算过程中水位边界条件不变。

2.2 计算模型

采用工程分析软件FLAC3D建立分析模型，以坝体平行轴线方向为Y轴，垂直地表方向为Z轴，水平方向为X轴，建立三维有限差分析模型，如图2所示。

图2 拦水坝心墙三维模型

在计算过程中，根据该工程的地质勘察报告、水文资料，计算力学参数取值如下：体积模量为30 MPa，剪切模量为10 MPa，重力方向为垂直向下，大小为10 m/s2，流体的密度为1 000 kg/m3，渗透系数(各向同性渗透模型)为10-10m2/Pa-sec，孔隙率默认为0.5，流体抗拉强度为-1010MPa。

2.3 计算结果分析

1)坝体应力分析。

图3～图6分别是坝体水位上升前后的大小主应力等值线图。水位高度的变化引起坝体大小主应力的分布情况发生了改变。应力分布主要特点是：起初应力分布沿坝轴线近似成对称分布，但是随着水位的变化，在坝体内部防渗心墙的作用下，坝体应力将进行二次调整；防渗心墙内部的大小主应力基本不变，而防渗墙附近，即防渗墙带和坝体连接处大小主应力变化较大，最大值达521 kPa。应力变化的原因是由于水位上升导致坝体砂石料产生湿陷固结的结果。

图3 初始最大主应力云图

图4 初始最小主应力云图

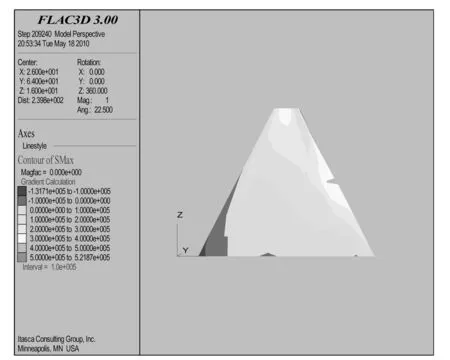
图5 最高水位的最大主应力云图

图6 最高水位的最小主应力云图

2)坝体位移云图分析。

图7～图10分别为初始应力、最高水位坝体垂直和水平位移等值线云图。图7和图9分别表示初始应力和最高水位的坝体垂直位移等值线云图；图8和图10分别表示初始应力和最高水位的坝体水平位移等值线云图。经过分析可以看到，最大竖向位移和最大横向位移均有所减小，有利于坝体的稳定。

图7 初始应力的z向位移云图

图8 初始应力的x向位移云图

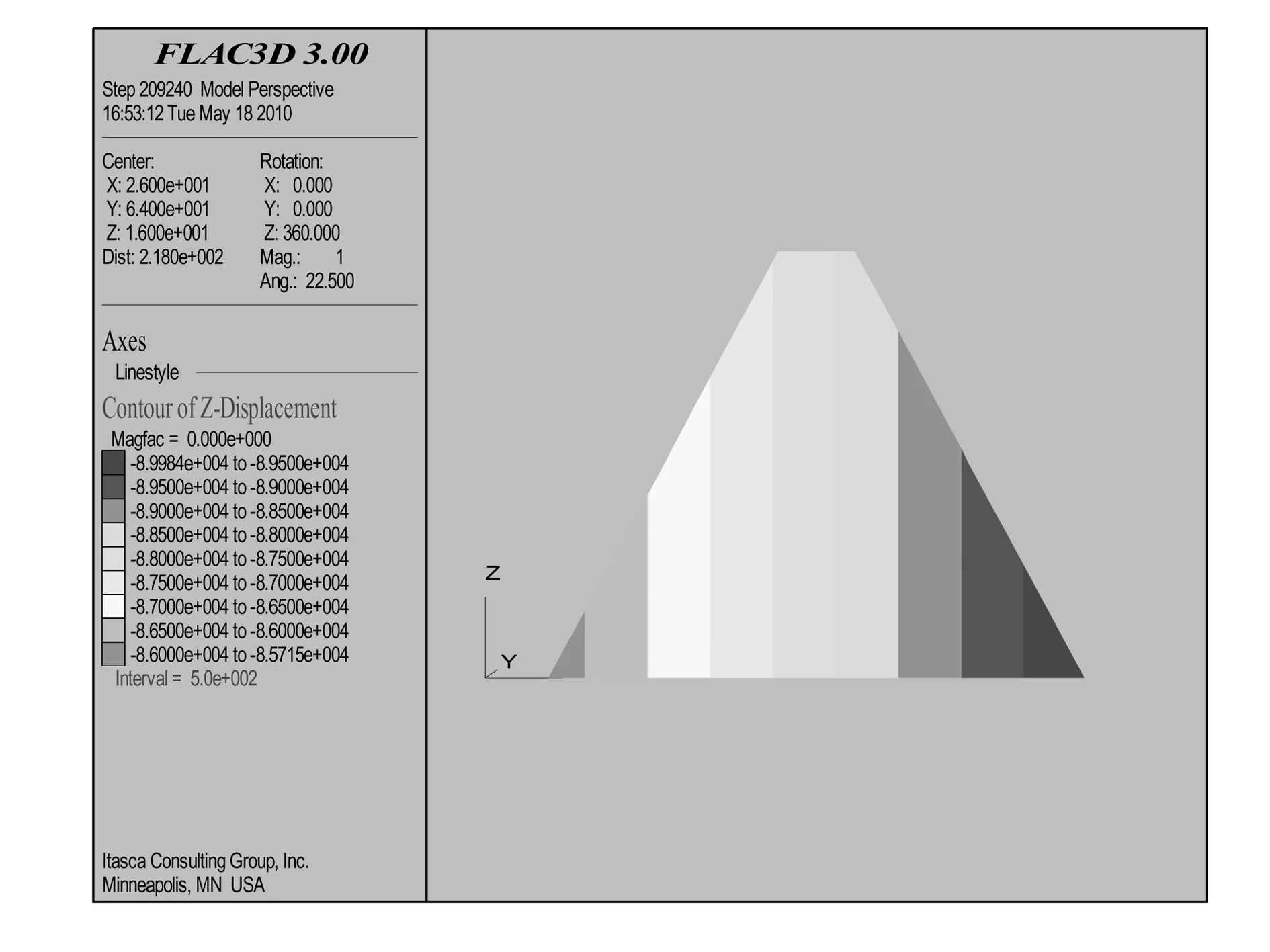
图9 最高水位的z向位移云图

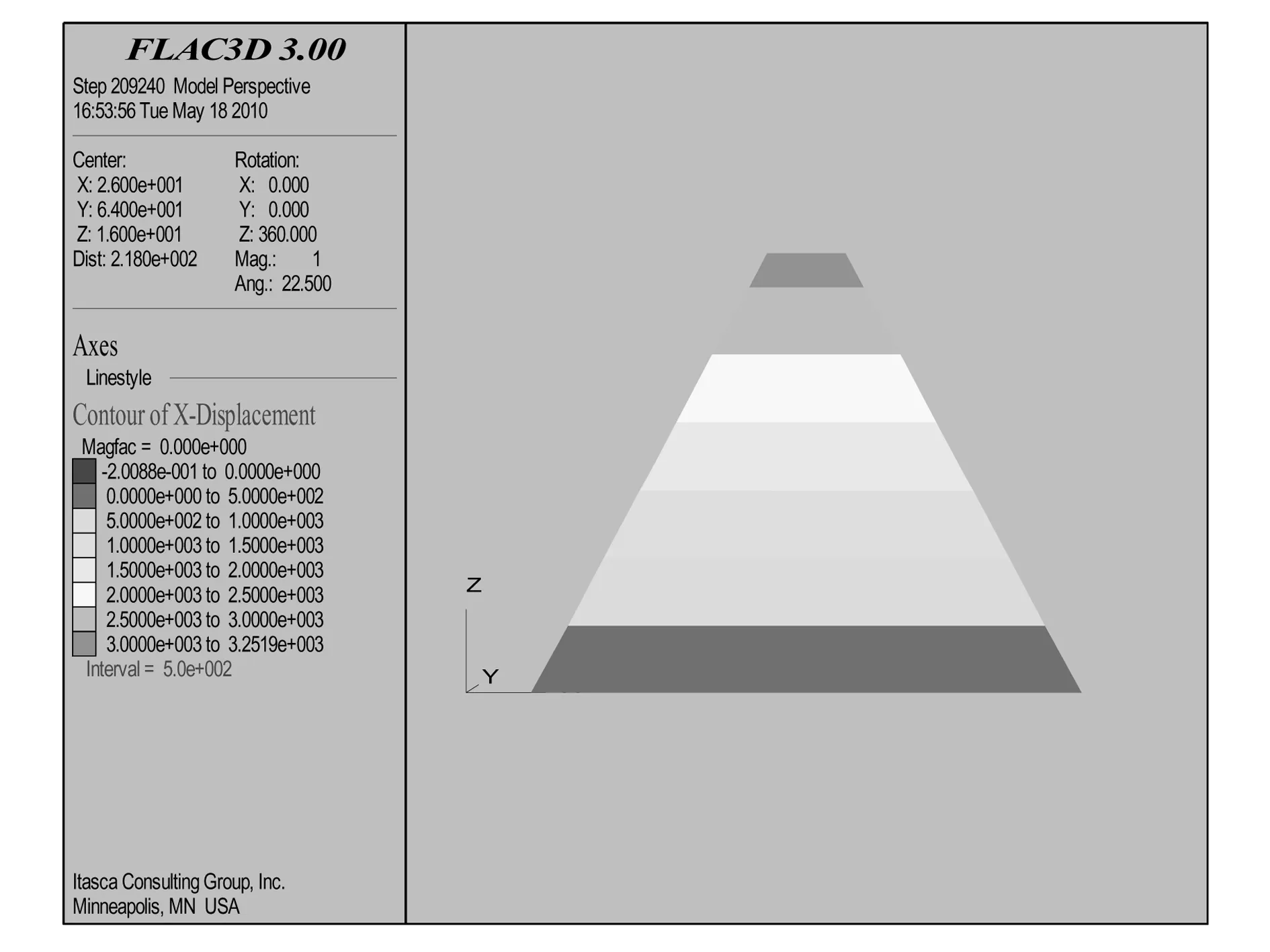
图10 最高水位的x向位移云图

3)坝体渗透孔隙水压力分析

图11、12分别为初始应力的孔压云图和最高水位坝体的渗透孔隙水压力云图。比较分析可知，在拦水坝体设置防渗心墙，可有效改善坝体的孔隙水压力分布，达到坝体防渗加固的要求。

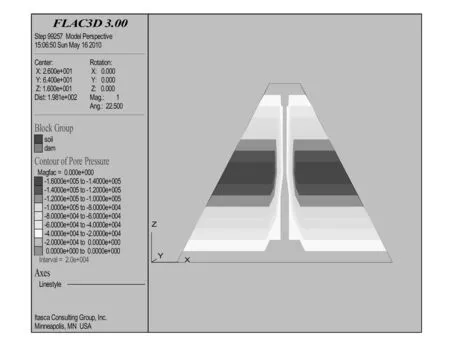
图11 初始应力的孔压云图

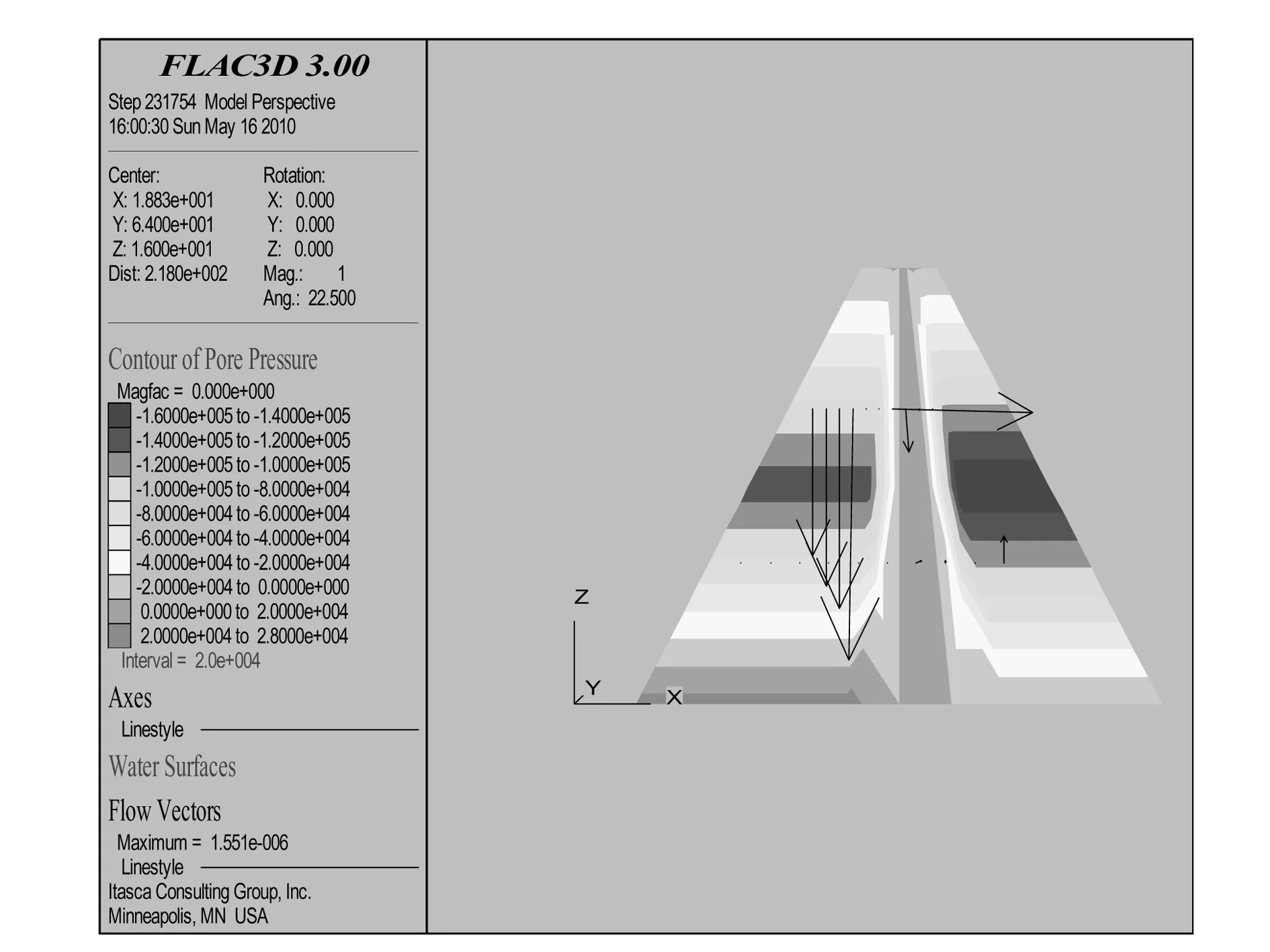
图12 最高水位的孔隙水压力云图

3 结论

1)心墙坝体在水载荷为零时，坝体的最大主应力和最小主应力近似对称地分布在心墙两侧。水位上升到最高点时，坝体主应力的最大值出现在左侧坝基处，应力水平等值线图显示了整个坝体处于安全稳定状态[9]。

2)应用FLAC3D软件对心墙土坝渗流过程进行分析，可以补充坝体弱应力区，调整大小主应力，改善坝体的稳定性。

3)三维快速拉格朗日分析方法可以较好地模拟土体材料的弹塑性力学模型[10]，与其它数值方法相比，该方法较简单，考虑影响因素少，并且计算结果与实际情况较接近。

[1] 张洪斌,孙永平,李万福,等. 本钢南芬拦水坝坝基渗透变形勘察[J]. 黑龙江水专学报, 2004, 31(1)：12.

[2] 项颜勇. 裂隙岩体中非饱和渗流与运移的概念模型及数值模拟[J]. 工程地质学报,2002,10(2)：204-209.

[3] 张国,朱济祥,庄军,等．岩质边坡稳定性的渗流耦合分析[J]. 天津大学学报,1999,32(5)： 560-564.

[4] 陈平, 张有天．裂隙岩体渗流与应力耦合分析[J]. 岩石力学与工程学报, 1994, 13(4)： 299-308．

[5] Oda M．An equivalent continuum model far coupled stress and fluid flow analysis in jointed rock masses[J]. Water Resources Research,1986(13)：1854-1865.

[6] 柴军瑞,仵彦卿．均质土坝渗流场与应力场耦合分析的数学模型[J]. 陕西水力发电, 1997, 13(3)：4-7.

[7] S Christensen, K R Rasmussen, K Moller. Prediction of regional groundwater flow to streams[J]. Groundwater, 1998, 36(2)：53-66.

[8] 陈晓平,茜平一,梁志松．非均质土坝稳定性的渗流场和应力场耦合分析[J]. 岩土力学，2004, 25(6)：860-864.

[9] 王祖强,张贵金,王明. 用FLAC3D模拟流固耦合评价病险土坝防渗加固效果[J]. 湖南水利水电, 2009(2)：41-43.

[10] 葛畅,张允亭. 本钢南芬拦水坝坝基渗透变形勘察-关于碎石类土的渗透变形试验[J]. 油气田地面工程, 2003(12)：37.