基于理想滑行路径的机场滑行道调度策略模型
牟德一,刘金凤
(中国民航大学 理学院,天津 300300)
0 引言
随着航空运输需求日益增长,飞机延误已成普遍现象,并有不断增长的趋势.据美国FAA研究表明,84%的飞机延误发生在地面,汉莎航空公司1999年由于飞机在空中等待降落而浪费了26000 t燃料[1].在我国的北京、上海、广州等大型机场,该问题也十分突出.飞机的地面延误主要发生在道面滑行,高峰时刻道面滑行冲突最为严重.由于扩大基础设施投资昂贵且短时间内难以实现,所以研究机场有限资源的整合优化,提高资源的合理利用率越来越重要.为了提高飞机滑行效率,减少地面滑行的等待时间,国内外学者做出了不同层次的研究,提出了多种解决方案.
在减少地面滑行时间,解决飞机滑行路径冲突问题上,一些学者试图从两个方面提出解决方案.一方面是为飞机确定无冲突的滑行路径,使飞机在停机位或跑道入口无限时等待并以最优放飞顺序放飞,J-P.Gotteland[2]和 B.Pesic[3]对这方面进行了研究,Sivakumar[4]以 Dall-Fort Worth 机场为例,运用混合整数规划进行分析,并将此模型应用扩展到任意机场的布局.另一方面是确定更多的无冲突的滑行路径,提供更多的无障碍路线.本文对第一种方案进行改进,同时兼顾第二种方法.即分散等待时间,把第一种方法的停机位或跑道入口等待转化为各个滑行道结点均可等待的新方案,这种做法在机场地面滑行指挥领域是允许的.此外,本文还采用了Floyd算法计算了多条无障碍路线,把最短路与理想路径严格区分,实现必要时安排优先级别较低的飞机按照次短路滑行,可以回避冲突,减少总调度时间,缓解机场地面忙碌状态.
1 飞机地面滑行调度问题
离港飞机从停机位到跑道出口,进港飞机从跑道入口到停机位所经过的路线称为飞机地面滑行路径.飞机地面滑行调度研究的主要目的是为空中交通管制员提供有效的滑行调度方案,以降低机场的地面滑行延误.
由于滑行过程要受到进离港过程给出的位置和时间上的约束,同时在庞大的滑行路径上进行滑行的进离港飞机也会发生各种冲突,突出表现为:追尾冲突——在同一条滑行路径上进港和离港的两架飞机相向滑行;相遇冲突——同一滑行路径上进港(或者离港)的两架飞机同向滑行或同一结点处两架飞机相遇(见图1).
通常情况下的一般作法是将交叉冲突看作结点冲突,把相遇冲突看作滑行边冲突,而追尾冲突既可以看作边冲突,也可以看作点冲突.因为如果在滑行速度保持不变的情形下,若两架飞机在滑行边相向滑行因间距不足而产生追尾冲突,则在构成该滑行边的两结点也会产生结点冲突,反之亦然.因此,本文只将冲突分为边冲突和点冲突.
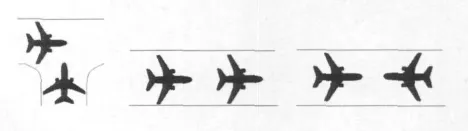
图1 三种类型相撞:交叉冲突(左),追尾冲突(中)和相遇冲突(右)
本文假设,所有飞机的优先级相同,即先到达结点先滑行原则.当时刻相等时,进港飞机优先于离港飞机,主要是为了减少进港飞机的空中等待时间,做到安全节油.
2 分散等待时间模型
为了更合理地利用机场滑行道资源,Sivakumar[4]与 Smeltink[5]以所有参加调度飞机的总滑行时间最短为目标:
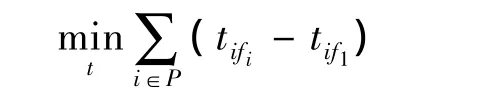
运用混合整数规划为每架飞机确定理想滑行路径,安排最优放飞顺序,让其他飞机在停机位或跑道入口无限时等待,为每架飞机找到到达且经过每个结点的时间,即.模型的目的是为每架飞机确定最短滑行路径,安排最优放飞顺序,确立滑行的初始时刻,滑行一旦开始滑行中途将不再停止.
固定时间段的飞机滑行时间指的是该时间段内所有滑行飞机的滑行时间总和;而调度时间是指该时间段内的第一架飞机开始滑行时计时,到最后一架飞机结束滑行时为止.通常,调度时间远小于滑行时间.目前涉及飞机地面滑行路径选择的研究中,如文献[4-5]等,大多以滑行时间最小为目标函数.显然,只有每架飞机选择了最短路才能达到滑行时间的绝对最短,但会导致多数飞机拥挤在最短路上,等待放飞.因此,从实际运用角度这种调度策略并不一定是最佳解决方案.因此本文将调度时间最短确定为目标函数,研究建立一种新的调度方案.
在实际的地面交通管制中,跑道出入口和滑行道的交叉点处是有等待线的(见图2),即滑行中的飞机为了避免冲突,保持相邻飞机之间的时间间隔或距离间隔,可以在等待线上等待,直到冲突消失为止.如此考虑,飞机在滑行路径的结点处就不再是一个固定的时刻,而很可能为一个时间段.比如,飞机在到达十字交叉结点后,发现前一个经过飞机还不满足时间间隔,就需要在结点处进行等待片刻,那么该飞机在此结点就要经历一个时间段.

图2 跑道和滑行道的等待线
因此本文引入两个时刻来表示飞机到达且经过该结点的时间:
下面对进离港飞机的特殊结点到达和离开时间进行特殊说明.
进港飞机:
第一个结点为滑行道入口,飞机到达该点的时间为飞机的进港时刻,离开该结点的时间为飞机接到指令开始滑行的时刻.即:=飞机着落时刻,=开始滑行的时刻;
最后一个结点为停机位,飞机到达该结点时间为实际到达时间,离开时间为无穷大(不考虑转机情形),在此模型中,设置为+整个研究的时间段即可.
离港飞机:
变量ziju=1表示飞机i在飞机j之前到达结点u,否则为0.
Tsep为滑行规定通过同一结点的两架飞机的时间间隔,一般因机型不同而有所差距.

3 确定多条无障碍路径的Floyd算法
上一节将滑行时间与调度时间区分开,下面将理想滑行路径与最短路径区分开.飞机最短路径是指地面交通网络上任意起始终止点间存在的多条路径中滑行距离最短或滑行时间最短的一条路径;飞机理想滑行路径是指在地面滑行调度中,以冲突最小,最终实现所有飞机调度时间最短为目标的路径,通常情况下是次短路.最短路径是飞机滑行的最基本路径,次短路径作为补充部分构成飞机滑行路径的理想路径.飞机只有按照理想滑行路径在机场地面交通网络上滑行才有助于网络上运行飞机的合理分布及网络上飞机流的动态均衡.
Floyd算法又称距离矩阵幂乘法.该算法在确定网络上任意两点之间的最短距离时,对有向和无向网络都是可行的.具体算法如下[6]:

计算次数p的确定:
(1)当wij≥0时,p由下式确定:P≥ln(n-1)/ln(2).这样的Dp就确定了网络各点间的最短距离.
(2)在其他情况下,如果出现Dk=D(k-1)或时,可取 p=k .
本文采用Floyd算法求出每架飞机的滑行路径之后,可以求出每架飞机到达最短路径上每个结点的时间.然后判断可能产生冲突的点和滑行边,并假设存在冲突的边为断路,再次采用Floyd算法求出新的最短路,即次短路,令优先级别较低的飞机避开高峰路段,选择次短路滑行.

图3 首都机声T2和东跑道部分简化图
以上是首都机场T2和东跑道的部分简化图,比如飞机i着落后要从跑道R7结点到停机位G217,可以为之确定多条理想路径:
①R7—T10—T11—T12—G217;
②R7—T10—T11—T27—G217.
在实际的滑行中就可以为飞机提供更多的选择,若此时恰好有飞机j在T10—T11中与其发生冲突,则可以假设T10—T11为断路,重新利用Floyd算法计算新的理想路径:
③R7—T10—T9—T26—T27—G217;
④R7—T10—T9—T11—T27—G217;
⑤R7—T10—T9—T11—T12—G217.
计算若将飞机甲在T10处等待若干秒后的滑行时间和绕行滑行时间相比较,采取总调度时间较短的方案执行.具体算法流程图如图4.

图4 算法流程图
图4为飞机到达滑行道任意结点A,而目的地设为F时的路径选择流程图.
4 模型计算与算例实现
本文采用首都机场T2和东跑道某天机场道面的滑行调度的实际数据进行研究,给出了某一高峰时刻15 min内在T2航站楼进行起降的10个飞机(见表1).针对以下3种方案进行了实验比较,主要包括总路长,滑行时间和调度时间,延误航班数等(见表2).

表1 航班计划

表2 验结果比较
方案1:以滑行时间最短为目标函数,确定飞机最短路径,使飞机在停机位或跑到入口无限时等待,以最优放飞数序放飞[4];
方案2:以滑行时间最短为目标函数,将等待时间分散到滑行中各个结点,避免停机位和跑道入口无休止等待;
方案3:以调度时间最短为目标,运用Floyd算法计算理想路径,确立多条无障碍路径,必要时绕开最短路,选择次短路,避开滑行高峰路段.
由此可以看出,方案2将等待时间分散到各个结点后,虽然总滑行时间不变,但是调度时间减少了,尤其是方案3中选择次短路后,回避了冲突,增加了滑行总路径和滑行时间,但是就总体调度来说,时间减少了,缓解了机场的忙碌状态,节约了调度时间.此外,进港飞机的空中等待时间减少,提高了机场跑道容量的实际利用率,在一定程度上,提高了航班的安全性.
比如一个机场年运行量30万架次,旅客吞吐量2700万的机场,如果每架飞机平均减少30 s的调度时间,那么每年就可以节省2500个飞机小时和22万多个旅客小时.这也说明了本文的模型不仅对机场滑行道高峰时刻飞机的调度是有效的,对于整个航空运输系统来说更是非常有意义的.
5 结论
本文在文献[4-5]的基础上,改进了目标函数,将滑行时间最短转化为调度时间最短,极大的缓解了机场地面滑行道的紧张状况.同时,Floyd算法的引入,提供了飞机滑行的多条无障碍路线,避免了最短路的拥挤,使机场资源得到最大限度的使用.
然而在本文的研究中为了问题的简化,忽略了机型的不同.实际的场面调度中,因机型的不同会产生飞机优先级的不同,最短安全间隔的不同,会增大问题的复杂度.因此,把飞机机型考虑在内是进一步研究的方向.
[1]刘兆明,葛宏伟,钱峰.基于遗传算法的机场调度优化算法[J],华东理工大学学报(自然科学版),2008,34(3):392-398.
[2]GOTTELAND J B,DURAND N,ALIOT J M,et al.Aircraft Ground Traffic Optimization[C].4th International Air Traffic Management R&D Seminar ATM 2001,Santa Fe,2001.
[3]PESIC B,DURAND N,ALIOT J M.Aircraft Ground Traffic Optimization using a Genetic Algorithm[C].Gentic and Evolutionary Conputation Conference GECCO 2001,San Francisco,2001.
[4]SIVAKUMAR RATHINAM,JUSTIN MONTOYA,YOON JUNG.An Optimization Model For Reducing Aircraft Taxi Times at The Dallas Fort Worth International Airport[C],26th International Congress of The Aeronautical Sciences,2008.
[5]SMELTINK J W,SOOMER M J,DeWaal P R,et al.An Optimisation Model for Airport Taxi Scheduling[C].Thirtieth Conference on the Mathematics of Operations Research,Lunteren,The Netherlands,2005.
[6]黄雍检,赖明勇,MATLAB语言在运筹学中的应用[M].长沙:湖南大学出版社,2005:75-84.
[7]VISSER H G,ROLING P C.Optimal Airport Surface Traffic Planning Using Mixed Integer Linear Programming[C].AIAA Aviation Technology,Integration and Operations(ATIO)Conference,Denver,CO,2003.
[8]BALAKRISHNAN H,JUNG Y.A Framework for Coordinated Surface Operations Planning at Dallas-Fort Worth International Airport,AIAA Guidance,Navigation,and Control Conferen-ce Hilton Head,SC,2007,20-23.
[9]郑洁,高剑明.机场地面作业调度问题研究[J],河北北方学院学报(自然科学版),2008,24(6):60-62.

