任意带任意投影面的平面坐标转换方法研究

方 杨

(中铁工程设计咨询集团有限公司,北京 100055)

在工程测量中,为了减小投影长度变形,通常需建立工程独立坐标系。工程独立坐标系仍采用高斯投影方法,但投影面不是标准的参考椭球面,而是选定的抵偿高程面,一般选择测区的平均高程面，投影带不采用国家6°带或3°带,而采用任意带,投影的中央子午线通常设在测区中央，这样就形成了任意带任意投影面的独立坐标系。在任意带任意投影面的计算中必然涉及坐标换带问题及椭球的变换问题,不同的椭球变换方法所得坐标结果不同。本文详细研究了各种椭球变换方法,椭球变换后计算大地坐标的不同方式及坐标换带计算,实现了任意带任意投影面的坐标换算。

1 椭球变换方法

选定任意的高程投影面,会引起标准椭球参数的变化。在某一测区或工程中,选择实际观测的某一点或者多个点归算得到的一个等效虚拟点作为基准点进行椭球变换,得到新的唯一椭球。假设椭球变换的基准点为P0(B0,L0,H0),投影面大地高为ΔH。常用的椭球变换方法会引起坐标系原点、椭球长轴及扁率的变化,但一般不会引起坐标轴的旋转和尺度的变化。

1.1 椭球膨胀法

椭球膨胀法仅椭球长轴变化,椭球扁率、平移、旋转、尺度参数均不变。一种以投影面大地高ΔH作为长半径的变化量,即

da=ΔH

(1)

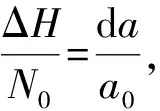
(2)

1.2 椭球平移法

椭球平移法仅椭球中心变动,即dX0≠0,dY0≠0,dZ0≠0,椭球长轴、扁率、旋转、尺度参数均不变。其值为

(3)

1.3 椭球变形法

椭球变形法使椭球长轴及扁率均变化,平移、旋转、尺度参数均不变,变化量为

(4)

2 椭球变换后计算大地坐标的两种方式

椭球参数变化后,新椭球面上的大地坐标也会有相应变化。计算新的大地坐标或者大地坐标变化量有两种方式。

2.1 大地坐标与空间直角坐标的关系

大地坐标与空间直角坐标间的关系式为

(5)

当椭球上一点大地坐标变化时,其对应的空间直角坐标保持不变。椭球变换后,首先根据原椭球参数由(5)式计算出一点的空间直角坐标,然后利用变换后的椭球参数求出新椭球面上的大地坐标。这样就完成了椭球变换后大地坐标的变换。

2.2 广义大地坐标微分公式

广义大地坐标微分公式为

(6)

式中,A、B、C、D的具体值参见文献[1]。代入不同的平移参数dX0,dY0,dZ0、旋转参数εX,εY,εZ、椭球几何元素da,df和尺度因子m,可算出不同的大地坐标变化量。

采用椭球膨胀法,根据式(7)可计算出各点大地坐标变化量

(7)

采用椭球平移法,根据式(8)可计算出各点大地坐标变化量

(8)

采用椭球变形法,根据式(9)可计算出各点大地坐标变化量

(9)

3 任意带任意投影面的坐标转换计算

(1)将第一带、指定高程投影面上的平面坐标(x,y,h)I换算为标准椭球面上的大地坐标(B,L,H)I。

若利用空间直角坐标和大地坐标的关系计算,其步骤为：①选择椭球膨胀法或椭球变形法,根据式(1)、式(2)、式(4)计算椭球长轴或扁率的变化量,并计算新的椭球参数a1=a+da,f1=f+df。②根据新椭球参数,利用高斯投影反算公式,计算新椭球上的大地坐标；③将新椭球上的大地坐标转换为空间直角坐标。④根据标准椭球参数将空间直角坐标转换为标准椭球上的大地坐标。

若根据广义大地坐标微分公式计算,其步骤为：①根据标准椭球参数和第一带中央子午线,按高斯投影反算公式,将第一带的平面坐标计换算为标准椭球上的大地坐标,其目的是为了后面计算大地坐标改正量；②选择一定的椭球变换方法,根据式(1)、式(2)、式(3)、式(4)计算椭球长轴或扁率或椭球中心的变化量；③根据式(7)、式(8)、式(9)计算出dB,dL,dH；④计算新椭球参数a1=a+da,f1=f+df,并根据新椭球参数和第一带中央子午线,按高斯投影反算公式,将第一带的平面坐标换算为新椭球上的大地坐标(B2,L2,H2)；⑤根据下式得到标准椭球上的大地坐标结果

B=B2-dB,L=L2-dL,H=H2-dH

(2)将第一步得到的标准椭球面上的大地坐标(B,L,H)I投影到第二带指定高程投影面上的平面坐标(x,y,h)II。

若利用空间直角坐标和大地坐标的关系计算,其步骤为：①根据标准椭球参数,将大地坐标(B,L,H)I转换为空间直角坐标。②选择椭球膨胀法或椭球变形法,根据式(1)、式(2)、式(4)计算椭球长轴或扁率的变化量,并计算新椭球参数。③根据新椭球参数,将空间直角坐标转换为新椭球上的大地坐标。④根据新椭球参数和第二带中央子午线,用上一步得到的大地坐标,按高斯投影正算公式计算第二带指定投影面上的平面坐标(x,y,h)II。

若根据广义大地坐标微分公式计算,其步骤为：①选择一定的椭球变换方法,根据式(1)、式(2)、式(3)、式(4)计算椭球长轴或扁率或椭球中心的变化量。②根据式(7)、式(8)、式(9)计算出dB,dL,dH。③计算新椭球参数a1=a+da,f1=f+df,及新大地坐标B2=B+dB,L2=L+dL,H2=H+dH。④根据新椭球参数和第二带中央子午线,用新椭球上的大地坐标(B2,L2,H2),按高斯投影正算公式计算第二带指定投影面上的平面坐标(x,y,h)II。

4 算例及分析

根据所给公式和计算步骤编制相应软件,并选取了某铁路工程中的部分点进行计算。该工程要求将中央子午线为129°、投影面大地高为500 m的平面坐标转换为中央子午线为130°、投影面大地高为350 m的平面坐标。本文分别采用了不同的椭球变换方法及不同的计算大地坐标变化量的方式进行坐标转换(限于篇幅,只列出了其中三点的转换结果)。基准点选择2号点。表1和表2分别是利用空间直角坐标和大地坐标的关系、广义大地坐标微分公式,不同的椭球变换方法求解的平面坐标结果。

表1 根据空间直角坐标和大地坐标的关系计算的平面坐标 m

表2 根据广义大地坐标微分公式计算的平面坐标 m

以2号点为基准,分别在原投影面和新投影面上求出各点至2号点的距离,将对应的距离相减得到长度变形值,其中两条边的结果见表3。长度变形值对比结果表明,采用不同的椭球变换方法得到的距离变形值基本相等,差距都在毫米级,说明采用不同的椭球变换方法所产生的距离变形是一致的。从限制长度变形的角度来说,各种椭球变换方法结果一致。

表3 不同方法计算的距离变形值 m

5 结束语

详细研究了任意带任意投影面的平面坐标换算,研究了不同的椭球变换方法和椭球变换后计算大地坐标的不同途径,给出了相应的计算公式,系统总结了坐标换算的步骤,并编制了相应软件,可为实际工程应用。根据工程实例分析了不同转换方法的结果。长度变形值的对比结果表明,各种椭球变换方法的结果一致。

[1]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2006

[2]邓兴升,汤仲安,花向红,等.椭球变换后的高斯投影正反算算法[J].大地测量与地球动力学,2010,30(2):49-52

[3]丁士俊,畅开蛳,高琐义.独立网椭球变换与坐标转换的研究[J].测绘通报,2008(8):4-6

[4]李世安,刘经南,施 闯.应用GPS建立区域独立坐标系中椭球变换的研究[J].武汉大学学报：信息科学版,2005,30(10):888-891

[5]施一民.适用于独立网的区域性椭球的确定方法及论证[J].解放军测绘学院学报,1994,11(2):88-93