螺栓连接结构的抗冲击简化算法*

陈 杨，孟庆芹，赵福燕

(南京船舶雷达研究所，南京 210003)

1 引言

抗冲击研究一直以来受到各军工行业的重视，尤以舰载、机载、车载设备对抗冲击的性能要求最高。国外舰船的抗冲击试验在上世纪60年代［1］就已经开始，而我国舰船的抗冲击研究从上世纪70年代才开始起步［2］，90年代以后加强了对该方向的研究，并关注舰船抗冲击的技术发展，近年来才开始对舰载设备的抗冲击能力进行研究。

在以往的舰载设备研究中，更多的是对设备结构所承受的静载荷和相当当量的动载荷进行验证分析［3］，即使进行抗冲击分析研究，也仅针对设备的结构本身，对各螺栓连接结构中螺栓的抗冲击研究较少。这主要是因为螺栓的受力复杂，模型建立的难度大，与设备耦合计算时会造成计算量大大增加。

2 抗冲击计算方法介绍

目前，舰载设备的抗冲击计算方法主要有3 种:静力法、时域法和频域法［4］。

(1）静力法，也称冲击因数法，由Buships 于1961年提出。它是将设备的重量与冲击因数的乘积来表示设备的冲击载荷，对设备进行静力学分析。该方法虽然计算简单，但实际上只针对设备的一阶响应进行了校核，并未考虑设备高阶响应产生的破坏，其计算局限性大。

(2）时域法，是用位移、速度和加速度与时间的函数模拟设备承受的冲击信号，将该函数作为冲击输入值，计算设备的冲击响应。其优点在于可以得到设备每一时刻每一节点的应力、应变值，适用于设备抗冲击详细阶段的计算，缺点是工作量较大。

(3）频域法，又称谱分析法，是将冲击谱作为设备的冲击载荷输入，对设备进行模态分析，并对计算结果进行合成，从而求得设备的冲击响应。频域法比时域法分析方便，但仅能够得到设备的最大受力情况的应力、应变结果，适用于设备抗冲击详细阶段的计算。

在实际工程设计中，针对螺栓连接结构中螺栓的抗冲击计算，采用上述任一方法均不能达到满意的结果。因此，本文结合上述3 种计算方法的优点，提出了一种针对螺栓连接结构的简化计算方法。

3 计算方法

该简化计算方法将静力法和时域法的优点相互结合，取消对模型的离散化处理，将螺栓结构处定义为柔性连接，在进行多体动力学计算后，再将柔性连接的受力情况与螺栓的结构强度进行校核。这样处理的好处是能够较为真实地模拟螺栓连接处的受力情况，且多刚体动力学方程求解更为简单，对时间和硬件的要求较低。

3.1 模型约束

为了简化螺栓连接结构模型，将螺栓连接结构简化为刚性体的柔性连接，在螺栓结构处定义柔性连接，产生一对与相对位移和相对速度成正比的三分量作用力，通过定义刚度系数、阻尼系数和预载荷来模拟真实的螺栓连接结构。同时，将结构本体定义为刚性体，简化其在强冲击作用下产生的变形效应。其具体计算方程如下［5］:

式中，x、y、z 表示3个方向的相对位移，θx、θy、θz表示3个方向的角位移，υ和ω分别表示相对速度和相对角速度，f和t 表示预载荷。

3.2 模型载荷

为了得到各个时刻的应力应变情况，将冲击谱转换为等效加速度谱，采用时域法对整个模型进行仿真计算。

参照国军标，水面舰船机械电子设备在不使用抗冲击隔离元件时采用的冲击谱如表1所示。对于安装在甲板上的设备，表中A0、V0按下列公式计算:

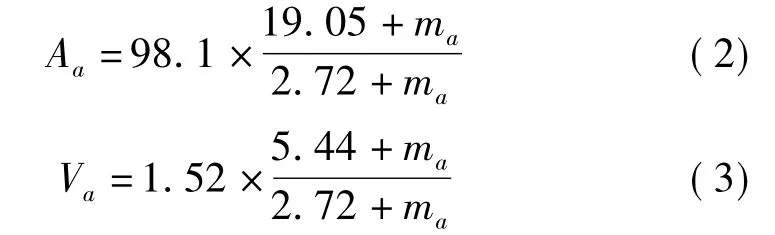
式中，ma为设备的模态质量，Aa为标称加速度谱，Va为标称速度谱。

表1 甲板设备各向弹性设计冲击谱

再将计算输入载荷转换为等效的时域加速度曲线，按照以下公式计算:

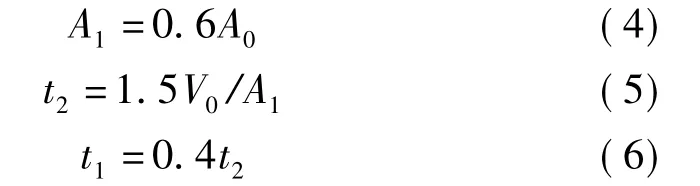
式中，A1为等效加速度峰值，t1为等效加速度峰值对应的作用时间，t2为等效加速度作用总时间。

3.3 数据处理方法

考虑到材料的特性限制，冲击载荷作用下结构响应的最大应力不得超过材料的静态屈服极限［6］，即满足

式中，n为失效系数，σbolt为螺栓连接结构受到的应力峰值，σs为材料静态屈服极限。

4 算例分析

本算例以某雷达天线产品为研究对象，根据上述抗冲击简化算法，对该产品基座螺栓连接结构的抗冲击能力进行仿真计算。

4.1 算例简介

借助多体动力学仿真软件MSC.ADAMS，将3个方向的时域加速度曲线用函数拟合而成，作用在雷达天线基座上，模拟出雷达天线在受到冲击响应后螺栓结构的受力情况，如图1所示。

4.2 约束和载荷

根据上述简化计算方法，在雷达天线基座螺栓结构处共设置15个柔性连接单元，定义刚度系数为2.1E+05(N/mm），阻尼系数为210(N*s/mm）。由于需要先计算柔性连接副的受力情况，再通过校核紧固件的强度的方法分析螺栓的抗冲击能力并在冲击计算前需要先进行静平衡计算，因此其连接副的预载荷设置对计算连接副的受力无任何影响，设置预载荷为零。而在雷达天线基座处设置的时域加速度谱可以由3.2节计算方法求得，具体参见表2所示。通过在计算模型上加载，对模型进行多体动力学计算。

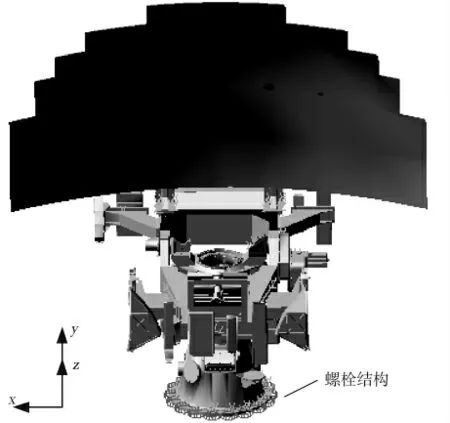
图1 雷达天线基座螺栓结构柔性连接示意图

表2 各向时域载荷参数

4.3 计算结果分析

图2 表示的是雷达基座结构响应加速度时历曲线，当冲击载荷作用时，雷达基座受到基座安装螺栓的束缚，产生响应运动。从图中可以看出，该冲击简化算法对设备的高阶响应的描述不清晰，但是对低阶的振动捕捉得十分准确。由于在设备的前期设计阶段，对高阶响应不是十分关注，因此该简化算法可以用于对设备设计初期的摸底计算。

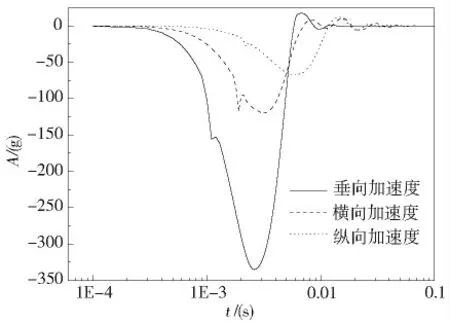
图2 雷达基座结构响应加速度时历曲线

图3 表示的是各螺栓结构单元失效系数对比。通过多体动力学计算后得到各柔性单元的受力情况，再与螺栓材料的静态屈服极限进行比较，折算出各螺栓结构单元的失效系数。从图2 可以看出，该雷达天线基座螺栓结构均能够满足表2的抗冲击要求，其中5号和12 号螺栓结构的拉应力失效系数较大。为了提高安全性，可以对该位置的螺栓作适当改进。

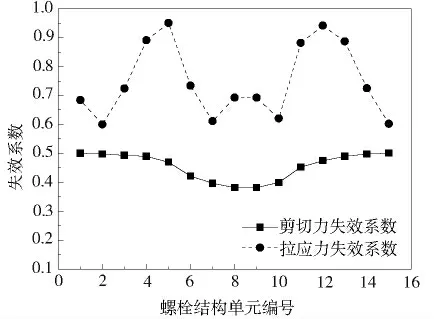
图3 各螺栓结构单元失效系数对比图

5 结束语

本文提出了一种新的螺栓连接结构的抗冲击简化算法。借助ADAMS 软件对模型进行多体动力学计算，得出螺栓结构的受力曲线，再与螺栓材料的静态屈服极限进行对比分析，得出设备中各螺栓结构的失效系数。通过对某雷达天线案例的计算分析，得出结论:该算法模型简单，计算量远远小于常用计算方法，适合在设计初期对设备螺栓结构抗冲击能力的摸底计算，大大提高设计人员的冲击仿真分析能力。

［1］FOREHAND W T.UNDEX testing:when，why ＆how it began［C］.Proceedings of the 70th Shock and Vibration Symposium，1999.

［2］陈继康，等.某艇水下爆炸试验资料汇编［G］.北京:第六机械工业部船舶系统工程部，1982.

［3］汪玉，华宏星.舰船现代冲击理论及应用［M］.北京:科学出版社，2005.

［4］冯维，徐青，吴广明.船体基座抗冲击研究现状［J］.中国舰船研究.2008，3(4）:6-9.

［5］李增刚.ADAMS 入门详解与实例［M］.北京:国防工业出版社，2006.

［6］陈海龙，姚熊亮，等.船用典型动力设备抗冲击性能评估研究［J］.振动与冲击，2009，28(2）:45-50.