带网状筋壁板弯曲中性层近似计算方法

边洪录，赵长喜，赖小明

（北京卫星制造厂，北京 100190）

0 引言

随着我国载人航天事业的发展，长期有人居住的空间站计划已经被列入日程。空间站主结构为大型密封舱结构，由整体壁板焊接而成。根据北京卫星制造厂现有壁板的制造流程，弯曲后的壁板外形不再进行机械加工，因此对于壁板的弯曲展开尺寸精度要求较高。确定壁板弯曲后展开中性层与弯曲内表面的距离（简称中性层位置）成为壁板制造过程中的关键步骤。

本文分析了整体壁板的结构特点，介绍了中性层位置计算的简化原则，通过计算确定了整体壁板中性层的位置，并与弯曲试验实测结果进行了比对，证明了该计算方法的有效性。这为今后结构近似的壁板展开计算提供了可靠的依据。

1 壁板的结构特点

整体壁板采用铝合金材料，材料牌号为5A06，其性能见表1。网格的长度和宽度均在150 mm左右。壁板弯曲后的内半径在500～3 000 mm之间；单块壁板的最大展开长度小于3 000 mm，其尺寸精度要求为±0.5 mm。

2 板材弯曲理论及假设

2.1 板材弯曲理论

板材在外界力矩的作用下，其变形区（图1中的ABCD区域）的曲率发生变化。在整个弯曲过程中，板材变形区外表面拉伸，内表面压缩。随着力矩的增大，板材弯曲程度逐渐增大，内部应力-应变变化可分为3个阶段：纯弹性弯曲阶段，弹塑性弯曲阶段，纯塑性阶段。各阶段板材变形区内部切向应力分布如图1中的(a)、(b)、(c)所示[1]。

图1 弯曲时板材变形区内部切向应力分布图Fig.1 Internal tangential stress distribution of curly plate material in deformation region

根据壁板结构特点可知，整体壁板弯曲变形区多处于弹塑性弯曲阶段。

2.2 壁板弯曲假设

由于板材弯曲过程中塑性形变方程较为复杂，

表 1 壁板材料性能表Table 1 Material properties of thin-walled plate

壁板为方形网格结构，主要包括腹板和加强筋两部分。腹板厚度为2.5～3mm；加强筋宽度为4～5 mm，高度约为17～17.5mm，壁板总厚度为20 mm。为了简化中性层位置的计算，在满足运算精度的同时，作出下述的假设：

1）假设壁板所采用的材料为理想塑性材料；

2）假设塑性弯曲时，壁板仍满足平面假设；

3）假设变形区内部弹性变形仍满足弹性弯曲理论；

4）假设壁板弯曲过程中应力中性层和应变中性层重合。

同时根据壁板的结构特点，对壁板沿弯曲线的剖面进行简化。由于壁板沿弯曲线的剖面实际上由数个变化的T型截面组成，因此根据对称原则，可将壁板沿弯曲线方向的剖面简化为单个T型截面。简化后的T型截面与原壁板T型截面的几何形心位置相同，其形状如图2所示。

图2 简化后的T型截面Fig.2 Reduced cross-section profile

3 中性层位置的计算方程建立

中性层位置的计算是建立在上述假设的基础上，即沿弯曲线方向的T型剖面形状不发生变化，其位置仅随弯曲角的变化而变化，且剖面上的总合力为零。

假设壁板弯曲半径为R，拉伸区域的合力为Ft，其面积为At；压缩区域的合力为Fc，其面积为Ac。根据本文第2节中的假设2），有：

将式(2)与式(3)代入式(1)，可得：

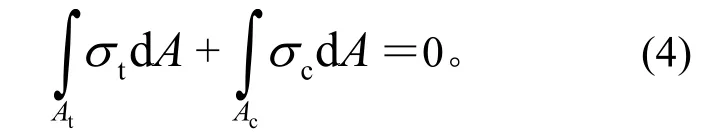
根据板材弯曲理论，假设壁板弯曲后的中性层半径为ρ，变形区内距中性层y处纤维的切向应变为[2]：

由式(5)可知，壁板变形区内的切向应变θε与距中性层的距离y近似成正比例关系。在中性层附近以弹性变形为主。若已知弹性变形阶段最大切向应变sε，则根据相似三角形关系，可确定壁板变形区内部弹性变形部分的厚度

式中sε为壁板弹性变形阶段产生的最大切向应变。结合上述分析结果及T型截面的几何特性，可知此时壁板变形区内的剖面上切向应力分布，如图3所示。

图3 壁板变形区沿弯曲线方向剖界面切向应力分布图Fig.3 Tangential stress distribution of cross section along curved line direction in plate deformation region

图中：yc为壁板中性层距弯曲内表面的距离；t为壁板厚度；σt、σc为壁板材料拉伸和压缩时屈服强度。

根据弯曲变形区内的几何关系，中性层弯曲半径可表示为：

由图3及假设1）可知，当壁板拉伸区域的最外侧和压缩区域的最内侧均处于塑性变形区域时，则有

根据图3中的几何关系，当壁板中性层两侧的拉伸和压缩区域处于弹性变形区域时，距中性层x处的应力为：

将式(5)～(9)带入式(4)，就可得到关于壁板中性层位置的计算方程。

4 中性层位置与弯曲半径的关系

本文采用MatLab软件进行编程求解中性层位置方程。求解思路如下：

1）根据截面形心位置和完全塑性弯曲状态下的中性层位置确定中性层位置的变化区间。

2）使用二分法假设中性层位置，并计算此位置下的切向合力。

3）判断合力是否为零。如果合力为零，则此位置为该状态下的中性层位置。

4）如果合力不为零，则利用二分法重新确定中性层位置，对上述计算过程进行迭代，直至找到切向合力为零。求解流程如图4所示。

根据中性层位置计算方程，对于截面形心位置距内弯曲表面的距离为 3.7 mm的壁板，通过MatLab软件求解并描绘出壁板中性层位置和弯曲半径的关系，如图5所示。

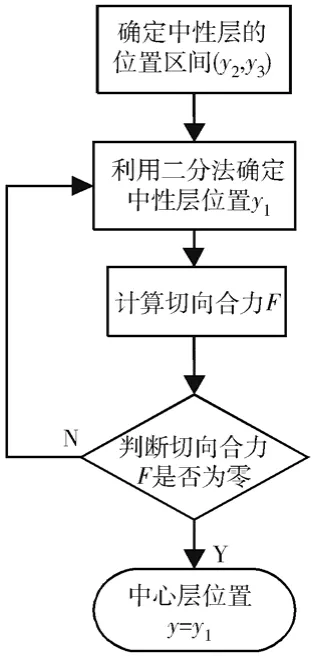
图4 中性层位置求解流程图Fig.4 Flow chart for solution of neutral layer

图5 中性层位置与弯曲半径的关系图Fig.5 Relationship between neutral layer position and bending radius

由中性层位置计算方程及图5可知：壁板弯曲过程处于弹塑性阶段时，中性层位置曲线为抛物线；当内弯曲半径R＜ 600 mm时，中性层位置基本不再发生变化，因此可以近似认为此时壁板弯曲已进入纯塑性阶段。

5 实测数据与理论计算结果的对比分析

壁板弯曲中性层位置的弯曲试验测量数据与计算结果列于表2。

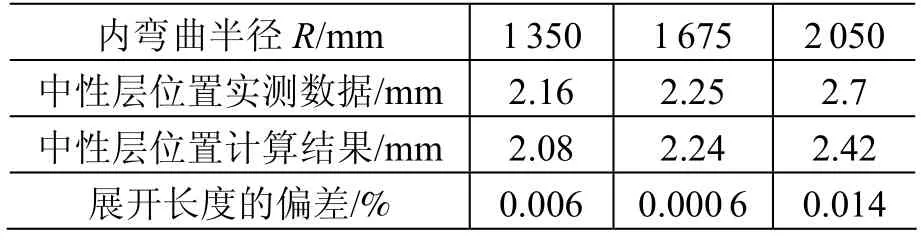
表2 中性层位置实测数据与计算结果对比Table 2 Comparison between measured data and computed result of the neutral layer’s location

式中：L实为实际展开长度；L理为理论计算展开长度；y实为实测的中性层位置；y理为理论计算的中性层位置；R为壁板的内弯曲半径。

由于材料、加工工艺和加工设备的限制，单块壁板的展开长度小于3 000 mm，因此展开长度误差小于0.42 mm，能够满足壁板展开的精度要求。

6 结论

本文通过对壁板弯曲过程的分析及中性层位置计算方程求解结果和弯曲试验实测结果对比分析，得到如下结论：1）壁板弯曲过程处于弹塑性阶段时，中性层位置曲线为抛物线；2）壁板弯曲中性层位置计算方程的计算结果能够满足现有产品壁板展开长度的精度要求；3）由于中性层位置方程的建立前提包含诸多假设，因此该方程的计算结果只是实际中性层位置的近似值。

（References）

[1]黄庆宝.板料成形及模具数值模拟分析[D].哈尔滨理工大学硕士学位论文, 2007

[2]胡世光.板材冷压成形原理[M].北京： 国防工业出版社, 1979