大跨度桥梁抗风技术挑战与基础研究

项海帆,葛耀君

(同济大学土木工程学院桥梁工程系,上海 200092)

1 前言

自1978年改革开放以来,经济的高速发展对交通基础设施建设提出了巨大的需求。在30年中建成的数以十万计的桥梁中,出现了为数众多的大跨度桥梁,已经建成的400 m以上跨度的桥梁有64座,其中包括18座悬索桥、36座斜拉桥和10座拱式桥。其中,最具代表性的4座大跨度桥梁是:1991年建成的423 m跨度的上海南浦大桥,是我国第一座跨度超过400 m的桥梁;2003年建成的上海卢浦大桥,以550 m的跨度创造了新的拱式桥世界纪录,获得了2008年国际桥梁及结构工程协会(International Association for Bridge and Structural Engineering,IABSE)杰出结构奖;2008年建成的世界最大跨度斜拉桥——苏通长江大桥,将斜拉桥跨度的世界纪录提高到1 088 m;2009年建成的1 650 m跨度的舟山西堠门大桥,是目前世界上跨度最大的钢箱梁悬索桥,并且首次采用新型分体式钢箱梁技术,提升了钢箱加劲梁悬索桥的抗风性能和跨越能力[1,2]。

随着桥梁跨径的不断增大,结构质量越来越轻、结构刚度越来越小、结构阻尼越来越低,从而导致了对风致作用的敏感性越来越大。文章主要介绍悬索桥颤振、斜拉桥拉索风雨振和拱式桥涡振等方面的抗风技术挑战以及基础研究中的桥梁风振精细化分析方法[1,2]。

2 悬索桥颤振及其控制

在过去的一个多世纪里,大跨度悬索桥的建设取得了举世瞩目的成就。在全世界已经建成的跨径排名前十的悬索桥中(见表1),中国占有5座,美国2座,日本、丹麦和英国各有1座。前4座悬索桥和香港青马大桥均存在着颤振或涡振等风振问题,需要采取控制措施来改善桥梁的抗风性能,例如,香港青马大桥和润扬长江大桥采用了中央稳定板,舟山西堠门大桥采用了分体双箱梁,明石海峡大桥采用了开槽加稳定板形式的桁梁,大海带桥采用了导流板等[3]。

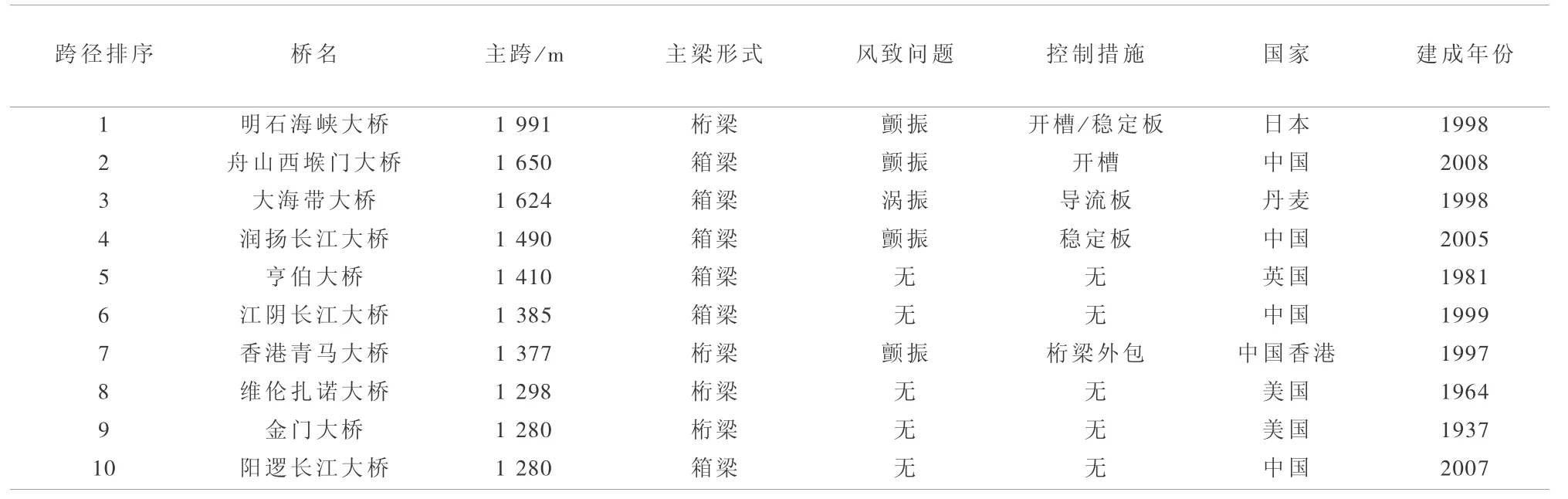
表1 世界跨径排名前十的悬索桥Table 1 The long span suspension bridges ranked in the top ten in the world

2.1 润扬长江大桥

2005年建成的润扬长江大桥是中国第二、世界第四大跨径悬索桥。该桥为典型的三跨简支悬索桥,跨径布置为510 m+1 490 m+510 m,如图1所示。加劲梁断面为传统的闭口钢箱梁,高3 m,宽36.3 m。桥面双向各3车道,每个车道宽3.75 m,桥面两侧各留出一道3.5 m宽的紧急停车带,如图2所示[3]。

根据润扬长江大桥结构参数,对桥梁动力特性进行了有限元分析,计算获得了侧弯、竖弯和扭转振型的对称及反对称基频,并与同样是钢箱梁的大海带大桥和西堠门大桥进行了比较,如表2所示。润扬长江大桥的竖弯和侧弯振动频率基本合理,但是扭转频率比其他两座悬索桥相对偏低,主要是由于钢箱梁梁高较小的原因[3]。

图1 润扬长江大桥立面图(单位:m)Fig.1 Elevation of Runyang Bridge across Yangtze River(unit:m)

图2 润扬长江大桥主梁横断面(单位:m)Fig.2 Cross section of box girder of Runyang Bridge(unit:m)

表2 钢箱梁悬索桥的基频Table 2 Fundamental natural frequencies of suspension bridges with box girder

为了研究江苏润扬大桥的气动稳定性,在同济大学TJ-1边界层风洞中进行了节段模型试验,几何相似比为1∶70,该风洞试验段宽1.8 m,高1.8 m,长15 m。第一阶段试验结果表明,原结构不能满足54 m/s颤振检验风速的要求。为了提高结构的颤振稳定性,需考虑采取气动控制措施。在进一步的节段模型试验中,在主梁断面上增设了中央稳定板(见图2)。为了确认节段模型风洞试验结果,又在同济大学TJ-3风洞中进行了全桥气弹模型试验,该风洞试验段宽15 m,高2 m,长14 m。节段模型试验(SM)和全桥气弹模型试验(FM)所获得的颤振临界风速如表3所示,通过比较可以发现两种试验的结果十分接近,而0.88 m高的中央稳定板(见图3)能有效地提高颤振临界风速,以满足抗风稳定性要求[3]。

表3 润扬长江大桥颤振临界风速Table 3 Flutter critical speeds of Runyang Bridge

图3 润扬长江大桥的中央稳定板Fig.3 Central stabilizer on the deck of Runyang Bridge

2.2 舟山西堠门大桥

舟山西堠门大桥作为浙江舟山连岛工程的主体工程,是跨越西堠门水道、连接金塘岛和册子岛的一座大跨度桥梁。桥址选在册子岛和金塘岛之间水道最窄的地方,约2 200 m宽。在靠近册子岛处有一个小岛,称为老虎礁,可以布置一个缆索承重桥梁的主塔。如果将三跨悬索桥的一个主塔设在老虎礁上,那么另一个主塔就要落在金塘岛的斜礁上。为了确定主塔在金塘岛上的位置,进行了多种跨径方案的比选,例如,当跨径为1 310 m时,金塘侧主塔基础将建在水下35 m处,跨径为1 520 m时水深仍有20 m,而1 650 m是保证主塔基础不在水下的最小跨径。为了避免水下基础施工,西堠门大桥设计方案最终确定为两跨连续的悬索桥,主跨1 650 m(见图4)。

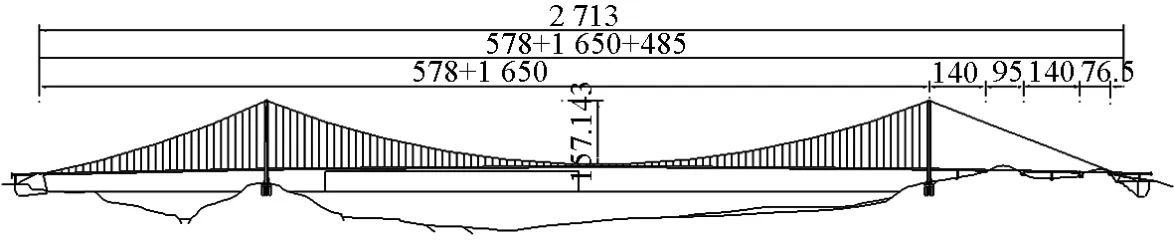
图4 舟山西堠门大桥立面图(单位:m)Fig.4 Elevation of Xihoumen Bridge in Zhoushan(unit:m)

主跨1 490 m的润扬长江大桥的颤振临界风速是51 m/s,主跨1 624 m的大海带桥的颤振临界风速是65 m/s,根据这些现有桥梁的经验来判断,1 650 m跨径的钢箱梁悬索桥将遇到颤振稳定性问题,更何况西堠门大桥的颤振检验风速要求更为严格,达到78.4 m/s。为此,在初步设计阶段提出了4种比选的箱梁断面,进行节段模型风洞试验。除传统的整体钢箱梁外,另外3种主梁断面形式分别为附加中央稳定板的单箱梁(见图5(a))、中央开槽宽6 m的分体双箱梁(见图5(b))和中央开槽宽10.6 m的分体双箱梁(图5(c))。其中,附加2.2 m高稳定板的单箱梁和两种分体双箱梁均能满足颤振稳定性的要求(见表4),最终采用了中央开槽宽6 m的分体双箱梁,并进一步优化成图5(d)所示的最终形式[3]。

图5 舟山西堠门大桥箱梁断面比选方案(单位:m)Fig.5 Alternative schemes of box girders for Xihoumen Bridge in Zhoushan(unit:m)

表4 舟山西堠门大桥的颤振临界风速Table 4 Flutter critical speeds of Xihoumen Bridge in Zhoushan

2.3 极限跨径悬索桥

作为人类的长久期待和梦想,超大跨度桥梁结构已经进入了一个新的发展时代,例如,意大利墨西拿海峡、中国琼州海峡、日本津轻海峡以及连接欧洲大陆和非洲大陆的直布罗陀海峡。作为最具挑战意义的桥梁跨径的极限,特别是悬索桥跨径的极限,一直是桥梁工程师们所关心的。为此,将5 000 m中跨和1 600 m边跨的三跨悬索桥进行了抗风概念设计[4]。为了提高加劲梁颤振稳定性,提出了两种断面形式,即不带稳定板的宽开槽断面(WS),如图6(a)所示,以及带竖向和水平稳定板的窄开槽断面(NS),如图6(b)所示。WS断面总宽80 m,选用4根主缆,而NS断面宽50 m,采用2根主缆[4]。

根据动力特性和风洞试验识别得到的颤振导数,并假定结构阻尼比为0.5%,采用多模态颤振分析方法计算求得了颤振临界风速。广义质量和广义质量惯矩以及颤振临界风速如表5所示。对于两种断面,虽然扭转与竖弯频率比随主缆矢跨比n的减小而稍微递减,但是颤振临界风速均随着n的减小而增大,出现这一现象的最主要原因是在颤振稳定性分析中广义质量特性的显著增加。WS断面和NS断面的最低临界风速分别为82.9 m/s和74.7 m/s[4]。

图6 宽开槽和窄开槽主梁断面的几何尺寸(单位:m)Fig.6 Dimensions of WS and NS cross sections(unit:m)

表5 主跨5 000 m悬索桥颤振临界风速Table 5 Flutter critical speeds of suspension bridge with a main span of 5 000 m

3 斜拉桥风振问题

目前世界跨径排名前十的斜拉桥如表6所示,其中7座在中国,1座在日本,1座在韩国,还有1座在法国。表6中,除了福建青州大桥由于采用钝体结合梁断面需要同时考虑颤振稳定问题外,全部斜拉桥均碰到了拉索风雨振动的问题,而且采用了一到两种振动控制措施,包括在拉索表面刻凹坑或加螺旋线,以及在拉索下端部安装机械式阻尼器[2,3]。

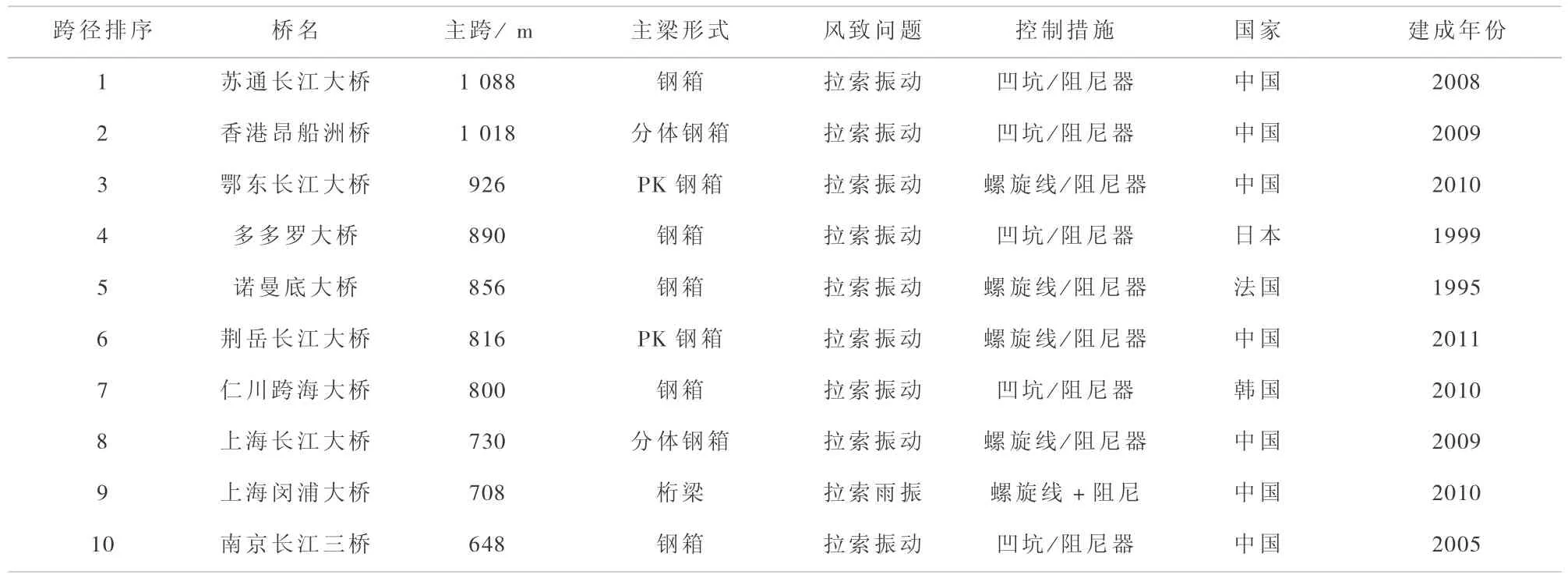
表6 世界跨径排名前十的斜拉桥Table 6 The long span cable-stayed bridges ranked in the top 10 in the world

3.1 千米级斜拉桥

2008年苏通长江大桥建成之前,世界最大跨度的斜拉桥是890 m的多多罗大桥。下面主要介绍已经建成或将要建成的主跨超过这一世界纪录的2座斜拉桥,即1 088 m苏通长江大桥、1 018 m的香港昂船洲大桥。苏通长江大桥共有7跨,其中主跨1 088 m,两边各有300 m+100 m+100 m的3个边跨。主梁断面为流线型正交异性钢箱梁,宽35.4 m,高4 m。桥面双向各3车道,每车道宽3.75 m,桥面两侧各设一道3 m宽的紧急停车带(见图7)。香港昂船洲大桥共9跨,其中主跨1 018 m为钢主梁,两边各有79.75 m+70 m+70 m+69.25 m的4跨混凝土主梁。钢主梁横断面为双流线型正交异性钢箱,宽2×15.9 m,高3.9 m。桥面双向各有11 m宽的三车道,两侧各有3.3 m的紧急停车带(见图8)[3]。

图7 苏通长江大桥单主梁横断面(单位:m)Fig.7 Cross section of single box girder of Sutong Bridge across Yangtze River(unit:m)

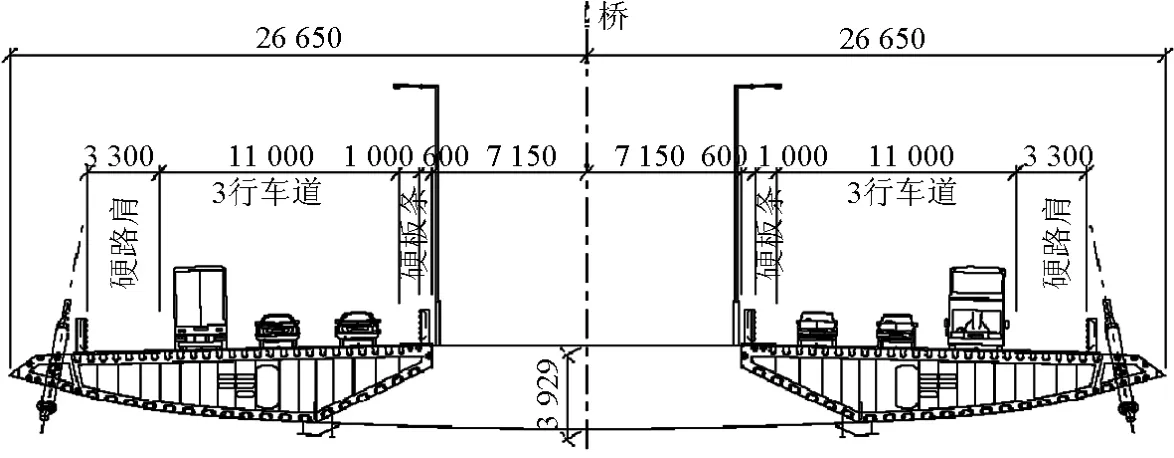
图8 香港昂船洲大桥双主梁横断面(单位:mm)Fig.8 Cross section of twin box girder of Stonecutters Bridge in Hong Kong(unit:mm)

3.2 斜拉桥的颤振稳定性

为了研究斜拉桥的动力特性,表7列出了5座主跨超过800 m的斜拉桥的侧弯基频、竖弯基频和扭转基频等参数。在这5座斜拉桥中,多多罗大桥是一个例外,该桥箱梁高度和宽度最小从而导致其基频最低,但是其扭转基频与竖弯基频的比值却最大。由于香港昂船洲大桥特有的分体双箱梁形式,该桥侧弯基频和竖弯基频排名倒数第二,但是扭转基频几乎与多多罗大桥和诺曼底大桥相等。作为跨度最长的斜拉桥,苏通大桥的扭转基频比其他4座斜拉桥都大,主要原因是桥宽大,斜索面的有利作用比较大[3]。

表7 斜拉桥基频和颤振风速Table 7 Fundamental natural frequencies and flutter critical speeds of cable-stayed bridges

颤振是最重要的抗风稳定性能,为了确定颤振临界风速,可以通过节段模型风洞试验或全桥气弹模型风洞试验方法,也可以基于试验识别的气动导数进行数值计算。检验风速是通过设计基准风速的修正而获得的。这5座桥的颤振临界风速和检验风速如表7所示。由于这些斜拉桥采用了空间索面和闭口钢箱梁,均不存在颤振失稳问题[3]。

3.3 拉索风雨振

表7所列的斜拉桥遇到的最普遍的抗风问题是长拉索在风和雨的环境下的振动。为此,分别对苏通大桥外径为139 mm拉索(采用最多)和158 mm拉索(最长索)的原型进行了节段模型风洞试验,并且在无雨和有雨两种条件下进行。风洞试验结果显示,两种拉索在风雨条件下的振动比干风条件下的振动要剧烈得多(见图9)[3]。

图9 干风和风雨条件下的拉索振动Fig.9 Cable vibration under dry wind and wind and rain

为了减小剧烈的拉索风雨振动,对拉索阻尼和振动频率进行了研究。不同的现场实测表明,拉索阻尼比平均值约为0.15%。为此针对0.12%到0.44%的5种阻尼比和1.0 Hz到2.6 Hz的4种振动频率进行了对比试验,如果能够将拉索阻尼比提高到0.30%,拉索风雨振动将得到有效的控制,而增大阻尼比可以采用基于不同机理的阻尼器,如油阻尼器、油粘性剪切型阻尼器、摩擦型阻尼器、高阻尼橡胶阻尼器、磁力阻尼器和电力阻尼器等[1]。控制风雨振动的另一种有效方法是防止拉索表面形成水线,因为水线是导致拉索风雨振动的直接原因。针对在拉索表面缠绕螺旋线和刻制凹坑两种气动措施进行了试验(见图10),结果表明两种措施都能有效地将振幅减小到允许值范围内[3]。

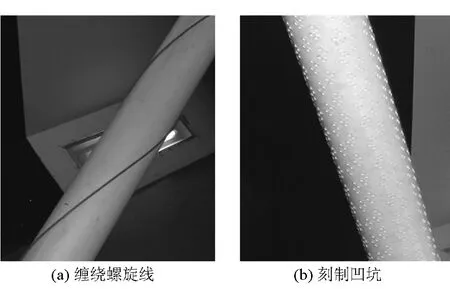
图10 阻止雨线生成的拉索风雨振动控制措施Fig.10 Countermeasures for preventing from rivulets to ease wind-rain vibration of stay cables

4 拱桥的涡激振动

世界跨度排名前十的拱桥如表8所示,其中只有上海卢浦大桥存在风致振动问题,即涡激共振,该桥涡激共振主要是由于拱肋的钝体横断面所造成的(见图11)。

表8 世界跨度排名前十的拱桥Table 8 The long span arch bridges ranked in the top 10 in the world

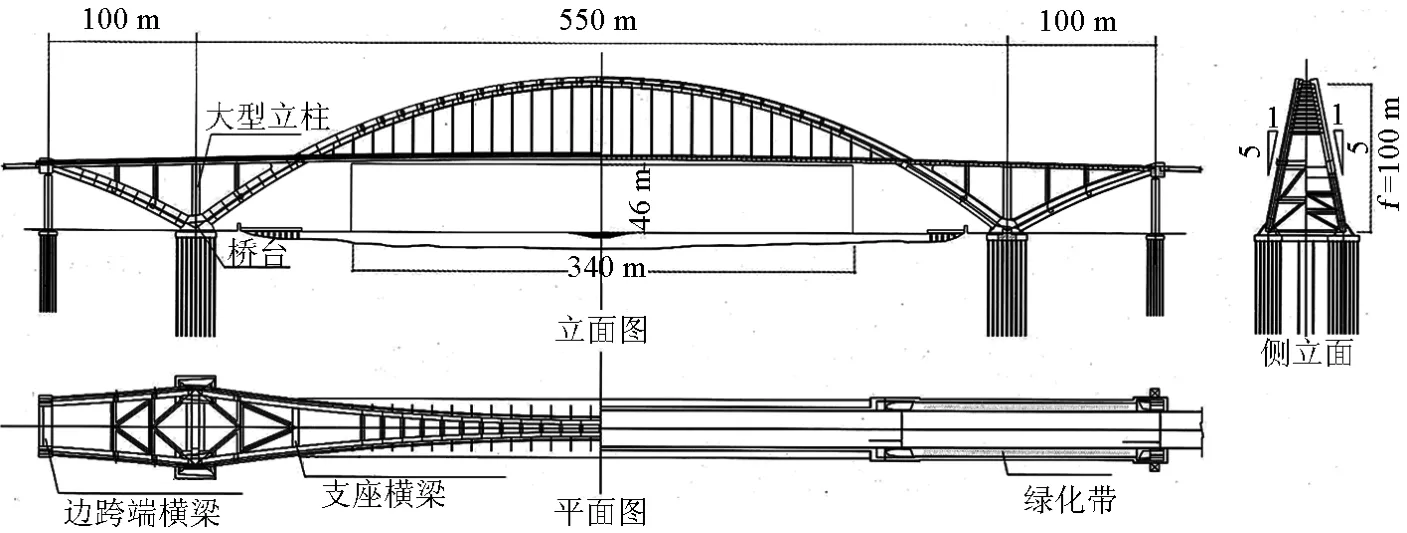
图11 上海卢浦大桥整体布置图(单位:m)Fig.11 General arrangement of Lupu Bridge in Shanghai(unit:m)

4.1 拱桥结构布置

上海卢浦大桥是一座中承式拱桥,跨径100 m+550 m+100 m,是当时世界上跨径最大的拱桥。桥面6车道,两侧各设一条观光人行道。主梁为正交异性钢梁,由拱肋连同吊杆和立柱共同支撑。在端横梁之间的主梁两侧各设有43根水平后张系杆,以平衡中跨拱肋内恒载引起的水平推力。整个钢拱-梁组合结构由拱肋、正交异性主梁、空间吊杆和立柱、拱肋间的横撑、以及水平后张系杆组成,如图11所示[3]。

两个倾斜的拱肋从拱脚到拱顶高100 m,单个拱肋横断面是经改良后的矩形钢箱,宽5 m,拱顶处高6 m,拱座处高9 m,如图12所示。这种外形导致了拱肋的竖弯和侧弯模态发生涡激振动,而且涡激振动在成桥状态和施工状态(拱肋最大悬臂阶段和拱肋合龙)均可能发生。为了确保拱肋和全桥在施工阶段和成桥状态的气动稳定性和安全性,基于桥址处的风环境特点,对卢浦大桥的涡激振动问题进行了深入研究[3]。

4.2 涡振数值模拟

应用同济大学2002年开发的离散涡方法程序RVM-FLUID[1]对双拱肋横断面二维模型进行数值分析,计算模型选用了平均高度为7.5 m的拱肋断面。计算结果表明,当Strouhal数(折减频率)St=0.156时,涡激振动的振幅可高达0.028倍于拱肋断面的高度。为了改善拱肋钝体断面涡激振动现象,针对图13所示的几种气动控制措施进行了数值试验比较,Strouhal数和相应振幅在内的计算结果如表9所示。包括 CS-2、CS-6、CS-7和 CS-8在内的4种方案能在一定程度上减小涡激振动振幅,其中,最佳的方案是全封闭隔流板(CS-8),该方案能将原结构的涡振振幅减小60%左右[3]。

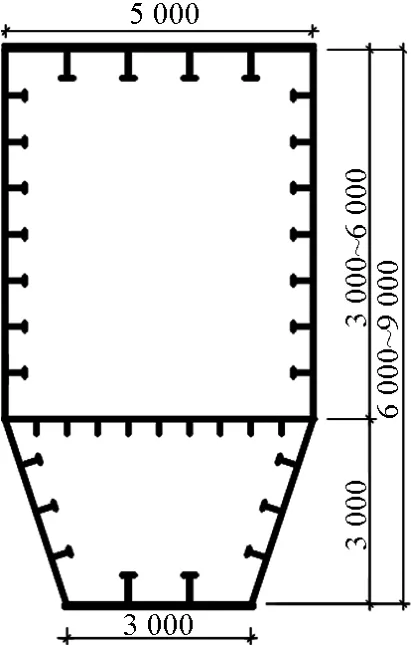
图12 拱肋横断面(单位:mm)Fig.12 Cross section of arch rib(unit:mm)

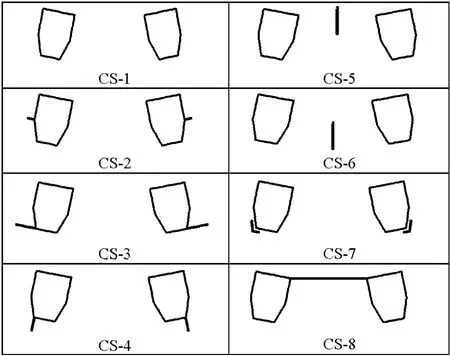
图13 拱肋涡激振动的控制措施Fig.13 Countermeasures of vortex induced vibration of arch rib

4.3 风洞试验验证

为了进一步检验全封闭隔流板的有效性,设计并制作了缩尺比为1∶100全桥气弹模型,除雷诺数外,其他无量纲参数均满足相似比的要求。上海卢浦大桥全桥气弹模型共模拟了3种施工状态:拱肋最大悬臂状态、拱肋合龙状态和全桥成桥状态。全桥气弹模型的涡激振动风洞试验是在同济大学TJ-3边界层风洞中进行的,如图14所示[3]。全桥气弹模型风洞试验结果表明,全封闭隔流板(措施A)和30%透空的隔流板(措施B)都能有效地减小涡振振幅[3]。

5 桥梁风振的精细化方法

同济大学从20世纪70年末开始桥梁抗风研究,通过80年代的学习与追赶,为1991年建成的我国第一座跨度超过400 m的大桥——上海南浦大桥抗风作出了重大贡献。经过90年代的提高和跟踪,有力支撑了我国第一座跨度超过1 000 m的特大桥——江阴长江大桥等桥梁的建设。进入21世纪后,面对特大桥梁建设的国家需求和桥梁抗风研究的学科使命,开展了创新和超越研究工作。经过30多年的全面跟踪和近10年的重点突破,形成了精细化的桥梁风振理论,其中包括:桥梁颤振的三维全模态精确分析方法和二维三自由度全耦合分析方法、桥梁抖振的任意斜交风分析方法和正确性的足尺实桥现场实测验证、桥梁颤振和抖振的随机性可靠度评价法。

5.1 三维颤振全模态精确分析

桥梁颤振是一种发散性的自激振动,传统的三维桥梁颤振频域分析方法基于结构模态叠加原理,需要人为选择几阶对颤振贡献较大的模态进行分析,所以称为多模态颤振分析法,该方法从20世纪70年代末提出一直沿用到20世纪90年代末。该方法主要缺陷有:在进行分析计算之前,需要人为指定多少阶模态和哪些模态参与了颤振;仅仅选择几个模态的组合往往只能是颤振模态的某种近似表达式,不可能是精确解;从理论上讲,选择的模态越多,叠加结果就越逼近精确解,但是多模态永远不可能是精确解[5]。

基于现代控制理论的状态空间法,将桥梁结构和周围气流作为一个整体系统,即振动方程描述的对象从结构拓展到系统,系统振动方程与传统的风荷载作为外荷载的结构振动方程分别表示为:

系统振动方程:

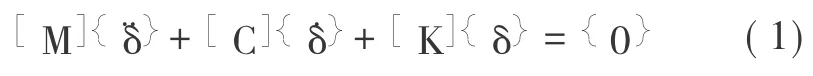
结构振动方程:

式(1)和(2)中,[M]为系统质量矩阵,下标 s表示结果,且[M]=[Ms];[K]为系统刚度矩阵,且[K]=[Ks]+[As];[C]为系统阻尼矩阵,且[C]=[Cs]+[Ad];[Ad]和[As]是非对称气动阻尼矩阵和气动刚度矩阵,所以[K]和[C]也都是非对称的,且结构响应具耦合特性;δ为结构位移向量,且 δ = φeλt,代入系统振动方程可得:

式(3)中,λ=μ+iω是系统复特征值,{φ}={ξ}+i{ξ}是系统复特征向量。显然,当所有复特征值的实部(μj)均为负时表明系统振动收敛,当有一对以上特征值的实部为正时系统颤振发散,而当只有一对特征值的实部为零时,系统处于临界状态,此时的风速即为颤振临界风速,而振动频率即为颤振频率。

引进一个附加方程后可以将二次特征值问题转化为如下2n组线性形式颤振运动状态方程:

由此可得全模态和多模态求解颤振临界状态的统一特征方程——正向和逆向标准特征方程:

正向标准特征方程(用于全模态精确分析):

逆向标准特征方程(用于多模态近似分析):

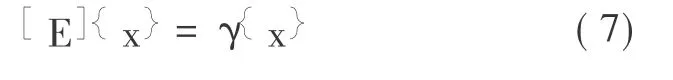
式(7)中,γ=1/λ为逆特征值。值得注意的是,矩阵[A]、[B]、[D]和[E]都是2n阶非对称矩阵。

提出了结合矢量逆迭代的QR转换矩阵方法,并直接用于求解正向标准特征方程——全模态分析方法,表10给出了悬臂平板桥、上海南浦大桥斜拉桥和瑞典Hoka Kusten悬索桥3座典型桥梁采用多模态颤振分析和全模态颤振分析的结果比较[5]。

表10 三维桥梁颤振多模态和全模态分析结果比较Table 10 Comparison of 3D flutter analysis results with multi-mode and full-mode methods

5.2 二维三自由度全耦合颤振分析

基于传统的桥梁颤振理论,桥梁颤振性能随施工阶段的演化规律只能采用气弹模型风洞试验方法进行研究,桥梁颤振机理及形态研究主要采用二维两自由度计算模型和二维节段模型风洞试验方法,桥梁颤振控制一般需要改变主梁断面的形式以便使得断面更具有流线型。

同济大学从虎门大桥和江阴长江大桥开始研究悬索桥施工阶段的颤振性能,20世纪末发现的瑞典Hoga Kusten悬索桥施工阶段颤振性能演化规律被大量引用[6]。该项研究首次系统涉及到了全部3种悬索桥梁段施工方法,即从跨中开始的对称拼装(Sequence A)和非对称拼装(Sequence B)以及从桥塔开始的对称拼装(Sequence C)。采用三维桥梁颤振分析方法得到了各个阶段的结构固有频率(见图15)和颤振临界风速(见图16),揭示了悬索桥固有频率和颤振性能随不同施工方法和梁段拼装率的演化规律,发现了从跨中开始的对称施工会在15%拼装率时出现临界风速的低谷,而从桥塔开始的对称拼装方法具有最好的颤振稳定性[6]。

图15 结构固有频率演化规律Fig.15 Evoluation of fundamental natural frequencies

通过引入不同自由度运动间的激励—反馈机制,建立了精确的二维三自由度全耦合颤振分步计算方法,提出了定量描述耦合颤振中各自由度参与颤振形态分析法,用于定量分析桥梁断面扭转、竖弯和侧弯3个自由度在颤振发生过程中的振动形态(自由度运动耦合效应)。在国际上率先将典型主梁断面归纳为5个大类13种形式(见图17),并较为全面和系统地研究了颤振驱动机理和颤振形态特征,揭示了气动负阻尼是桥梁颤振唯一驱动机理,发现了颤振形态主要取决于弯曲与扭转自由度的参与程度[7]。

结合工程实际研发了风嘴、开槽、稳定板、裙板和检修轨道移位等颤振控制措施,并采用二维和三维桥梁颤振分析方法揭示了这些措施的气动控制原理,同济大学承担完成了我国采用颤振控制措施的大多数桥梁抗风研究项目(见表11)。

图16 颤振临界风速演化规律Fig.16 Evoluation of flutter critical speeds

图17 5个大类13种典型主梁断面形式Fig.17 Thirteen typical bridge deck cross sections divided into 5 types

表11 我国采用颤振控制措施的桥梁抗风研究项目Table 11 Projects of wind resistance on bridges using flutter controlling measures in China

5.3 斜风作用下抖振的频域分析

桥梁抖振是指结构在自然风脉动成分作用下的随机性强迫振动,是一种限幅振动。桥梁抖振理论和方法主要是指确定抖振响应和评价抖振刚度或强度失效的理论和方法。传统的确定桥梁抖振响应最有效的方法是基于正交风作用计算模型的三维桥梁抖振计算方法和有效性验证的基于缩尺模型的三维全桥模型风洞试验方法。从理论上讲,作用于桥梁结构上的风荷载与桥梁轴线是任意斜交的,传统的正交风作用模型只是一种简化;采用全桥模型风洞试验方法进行有效性验证也只是一种过渡,理论方法的正确性验证必须采用实桥现场实测结果。

图18 香港青马大桥主梁跨中加速度计算和实测结果比较Fig.18 Calculation and measured results of accerations at the mid-span girder of Tsing Ma Bridge in Hong Kong

通过引入与桥轴线斜交的顺风向斜气动片条模型,提出了任意斜风作用下大跨度桥梁抖振响应频域分析方法及其基本理论框架[8]。该方法已成功应用于南京长江三桥和香港青马大桥的斜风抖振研究中。图18和图19表示在台风森姆作用下青马大桥主梁跨中加速度计算和实测结果的对比,其中风攻角2.25°,风偏角29.15°,风速17.1m/s。参数分析研究发现:最不利的抖振响应常在斜风下发生,法向风最不利的传统观点可能会造成不安全的结果,由此也证明在大跨桥梁抖振性能研究中考虑斜风效应是非常必要的[9]。

图19 香港青马大桥主梁跨中位移随风偏角变化曲线Fig.19 Skew wind angle vs.displacement at the mid-span girder of Tsing Ma Bridge in Hong Kong

5.4 桥梁风振可靠性评价

传统的桥梁颤振和抖振评价方法完全采用确定性安全系数方法,对颤振的评价主要依据综合安全系数K的大小,对抖振的评价主要比较抖振响应的数值与结构强度或刚度允许值的大小,不适合于随机性较大的桥梁抗风评价。在国际上首次提出了缆索承重桥梁风振可靠性评价体系——桥梁颤振失稳和桥梁抖振失效可靠性评价方法[10]。

在桥梁颤振失稳可靠性理论中,颤振极限状态方程可以表示为临界风速抗力减去设计风速效应,提出了设计风速概率模型和临界风速概率模型:

设计风速概率模型:

临界风速概率模型:

式(11)和(12)中,Gs表示阵风系数,服从正态分布;Ub表示年最大风速,服从极值I型分布;Cw表示风速换算系数,服从均值为1的正态分布;Uf表示基本颤振临界风速,服从对数正态分布。建立了基于一次或二次二阶矩可靠度理论的桥梁颤振失稳概率计算方法,成功应用于14座大跨桥梁中(见表12)[10],表12中β是可靠指标,Pf是相应的失效概率。

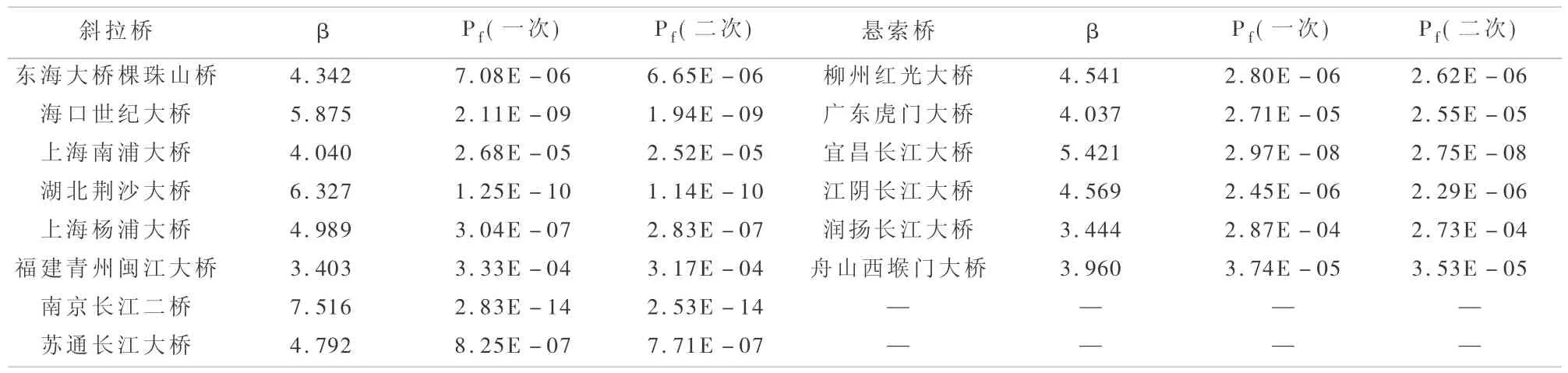
表12 桥梁颤振失稳可靠性评价计算结果Table 12 Calculation results of reliability evaluation for bridge flutter instability

采用结构动力可靠性基本模式——首次超越失效,提出了多自由度体系基于超越时间可靠性分析的Poisson过程法和Markov过程法以及基于超越极值可靠性分析的Rayleigh分布法和Gauss分布法,应用于桥梁抖振刚度或强度失效的可靠性评价,表13给出了上海杨浦大桥和江阴长江大桥的计算结果[10]。

表13 桥梁抖振刚度或强度失效概率计算结果Table 13 Calculation results of reliability evaluation for bridge buffeting stiffness or strength failure

6 结语

根据近年来建成的大跨度悬索桥的经验,无论采用流线型钢箱梁还是透风性较好的钢桁梁,由颤振稳定性控制的悬索桥跨径上限约为1 500 m,超过甚至接近这一上限时,设计者必须采取措施改善加劲梁的抗风稳定性,其中有效的措施包括在加劲梁上设置竖向或水平稳定板和中间开槽以及被动和主动控制措施等。初步研究表明,宽开槽断面或带竖向和水平稳定板的窄开槽断面能保证主跨5 000 m的悬索桥满足世界上大多数地区的抗风稳定性需求。实践证明:空间索面和流线型钢箱梁的千米级大跨度斜拉桥仍具有足够高的颤振临界风速,其主要抗风问题是长拉索的风雨振动;从抗风稳定性角度来看,随着拉索风雨振动控制措施的不断完善,斜拉桥主跨跨径还有一定的增长空间。在10座最大跨径拱桥中,只有一座出现了涡激振动的抗风性能问题,这一事实说明,拱桥跨径的增大还没有受到结构抗风性能的影响,但也许会受其他因素的制约,如静力稳定性、水平推力、施工技术等。

特大跨度桥梁风振的精细化理论是对传统理论的拓展,在三维桥梁颤振分析方面将近似的多模态分析拓展到了精确的全模态分析,实现了悬索桥施工阶段颤振性能演化规律、典型主梁断面颤振驱动机理和多种颤振控制措施原理的精细化;将桥梁抖振理论分析从正交风作用拓展到了任意斜交风作用,并完成了理论分析结果从模型风洞试验验证到实桥现场实测验证的拓展;初步建立的缆索承重桥梁风振可靠性评价方法,将确定性安全系数评价法拓展到了随机性可靠度评价法。今后应当继续深入进行风振理论精细化、桥梁风振机理和可靠性评价等方面的基础性研究,同时要积极开展计算流体动力学(computational fluid dynamics,CFD)技术和数值风洞以及桥梁等效风荷载方面的创新性研究,为未来跨海工程中的特大跨度悬索桥、斜拉桥和拱桥的风振控制做好准备。

[1]项海帆,葛耀君,朱乐东,等.现代桥梁抗风理论与实践[M].北京:中国交通出版社,2005.

[2]Ge Yaojun,Xiang Haifan.Great demand and various challenges—Chinese major bridges for improving traffic infrastructure nationwide[C]//Keynote Paper in Proceedings of the IABSE Symposium 2007 on Improving Infrastructure Bringing People Closer Worldwide.Weimar,Germany,2007:9-12.

[3]Ge Yaojun,Xiang Haifan.Aerodynamic challenges in long-span bridges[C]//Keynote paper in Proceedings of the Centenarey Conference of Institute of Structural Engineering.Hong Kong,China,2008:89-109.

[4]Xiang Haifan,Ge Yaojun.On aerodynamic limit to suspension bridges[C]//Keynote Paper in Proceedings of the 11th International Conference on Wind Engineering.Texas,USA,2003:81-95.

[5]Ge Yaojun,Tanaka H.Aerodynamic flutter analysis of cable-supported bridges by multi-mode and full-mode approaches[J].Journal of Wind Engineering and Industrial Aerodynamics,2000,86:123-153.

[6]Ge Yaojun,Tanaka H.Aerodynamic stability of long-span suspension bridges under erection[J].Journal of Structural Engineering,ASCE,2000,126:1404-1412.

[7]Xiang Haifan,Ge Yaojun.Refinements on aerodynamic stability analysis of super long-span bridges[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90:1493-1515.

[8]Zhu L D,Xu Y L.Buffeting response of long-span cable-supported bridges under skew winds[J].Journal of Sound and Vibration,2005,281(1-3):647-697.

[9]Zhu L D,Xu Y L,Xiang H F.Tsing Ma bridge deck under skew winds-Part II:Flutter derivatives[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90(7):807-837.

[10]Ge Yaojun,Xiang Haifan,Tanaka H.Application of a reliability analysis model to bridge flutter under extreme winds[J].Journal of Wind Engineering and Industrial Aerodynamics,2000,86:155-167.