基于经验模态分解和小波变换声发射信号去噪

于金涛，赵树延，王 祁

(1.哈尔滨工业大学自动化测试与控制系，150001 哈尔滨，hityjt@sina.com;2.哈尔滨商业大学计算机信息与工程学院，150028 哈尔滨)

基于经验模态分解和小波变换声发射信号去噪

于金涛1，2，赵树延1，王 祁1

(1.哈尔滨工业大学自动化测试与控制系，150001 哈尔滨，hityjt@sina.com;2.哈尔滨商业大学计算机信息与工程学院，150028 哈尔滨)

为了解决声发射信号去噪问题，在分析经验模态分解去噪和小波阈值去噪优缺点的基础上，提出将二者相结合的去噪方法，包括IMF-Wavelet方法，EMD-Wavelet方法和Wavelet-EMD方法.利用标准信号及断铅模拟声发射信号对所研究方法进行了去噪性能分析.结果表明:对于标准信号，Wavelet-EMD方法无论在高信噪比还是低信噪比情况下，都具有较稳定的去噪效果;小波阈值去噪对声发射信号去噪效果不理想，EMD-Wavelet和Wavelet-EMD方法对于声发射信号去噪效果较稳定.

经验模态分解;小波变换;阈值;去噪;声发射

声发射信号含有大量与缺陷性质相关的信息，但同时也掺杂着各种干扰和噪声，从背景噪声中识别出微弱的缺陷信号一直是个难题.对于由偶然因素引起的脉冲干扰噪声很容易通过限幅滤波法、中值滤波法和算术平均法等方法去除［1］.而对于被检测材料内部产生的一些在时域上看似随机分布的背景噪声，为检测缺陷带来困难.另外在声发射波传播的各个环节也极易引入各种噪声，包括因检测系统和各种原因引起的回路噪声，如前置放大器引起的电子噪声及因加载装置在加载过程中的相对机械滑动引起的摩擦噪声等，这些复杂噪声对声发射信号的影响更为严重，信噪比恶化问题更为突出，已成为制约着声发射检测和评价技术可靠性提高的关键因素之一.因此，声发射信号去噪是声发射信号处理的重要步骤，采用有效的去噪预处理技术提高信噪比，有利于提高后续声发射信号处理的精度.

小波分析具有良好的时频局域性，特别适合于非平稳信号的分析，在信号去噪领域得到了广泛的应用［2－3］，但是小波去噪方法也存在一些缺点，如去噪效果与信号特点及小波基函数有很大关系，当信噪比较小时，去噪效果不理想等.经验模态分解(Empirical mode decomposition，EMD)方法是由Huang［4］等于1998年提出的一种新的数据处理方法，它的特点是能够对非线性、非平稳信号进行线性化和平稳化处理，并在分解的过程中保留数据本身的特性.EMD方法最大的优点是基于信号本身的时间尺度特征，无需选择基函数就可把复杂信号由精细尺度到粗大尺度分解为若干本征模态分量(Intrinsic mode function，IMF)和一个余项，精细尺度分量频率最高，其余分量按频率高低依次排列.在基于EMD的信号消噪方法研究方面也取得了不少成果［5－7］，克服了小波去噪需要选择基函数的缺点，但是 Boudraa等［8］对EMD消噪算法和小波阈值消噪算法进行比较发现，EMD消噪算法效果整体上不如小波阈值消噪算法.本文将EMD去噪和小波阈值去噪结合起来，充分发挥各自的优点，并且利用标准信号和声发射信号进行了仿真验证.

1 经验模态分解及去噪原理

1.1 经验模态分解

在EMD方法中，Huang定义本征模态分量为满足以下2个条件的函数或信号:1)在整个数据序列中，极值点的数量与过零点的数量必须相等或者至多相差1个.2)在任何一点，由数据序列的局部极大值点确定的上包络线和由局部极小值点确定的下包络线的均值为零，即信号关于时间轴局部对称.

EMD分解的本质是一个筛选过程，对信号x(t)进行 EMD 分解的具体步骤如下［5－6］:1)求取x(t)的全部极大值和极小值点，利用三次样条函数分别拟合为该信号的上下包络线，计算两包络线的均值m1(t)及x(t)和m1(t)的差值h1(t)，h1(t)=x(t)－m1(t)，判断h1(t)是否满足IMF的2个条件，如果满足则令h1(t)为x(t)的第1个IMF分量imf1(t)，即imf1(t)=h1(t)，求出原信号与该 IMF的差值r1(t)，r1(t)=x(t)－imf1(t).2)如果h1(t)不满足IMF条件，则将其作为新的信号序列，重复1)，求均值m11(t)及h1(t)与m11(t)的差值h11(t)，h11(t)=h1(t)－m11(t)，对h11(t)重复上述步骤k次，直到h1k(t)满足IMF的条件，则令h1k(t)为x(t)的第一个IMF分量，imf1(t)=h1k(t)，求出原信号与该IMF的差值r1(t)，r1(t)=x(t)－imf1(t).3)把r1(t)作为新的信号序列重复1)、2)，逐次提取出第2、3直至第n个IMF分量，imf2(t)，imf3(t)，…，imfn(t);r2(t)=r1(t)－imf2(t)，…，rn(t)=rn－1(t)－imfn(t)，此时rn(t)为1个单序列，不再包含任何模态的信息，为原始信号的残余项.

经过分解后，原始信号可表示为

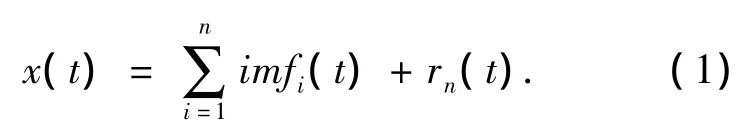
可见EMD可将任何一个信号x(t)分解为n个基本模态分量和一个残余项之和，分量imf1(t)，imf2(t)，…，imfn(t)分别包含了信号从高到低不同频率段的成分，rn(t)则表示信号x(t)的中心趋势.

1.2 经验模态分解去噪原理

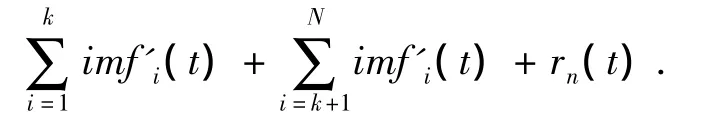
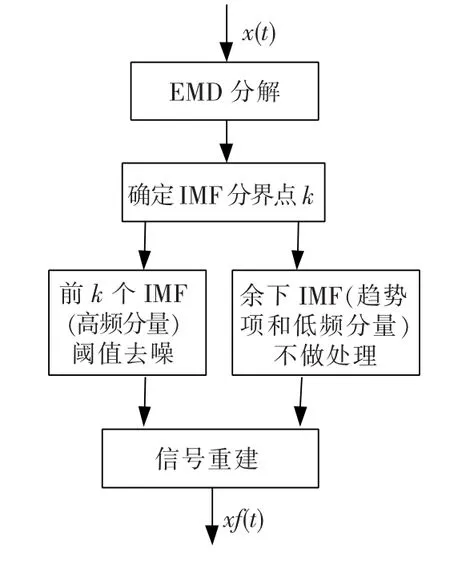
图1 EMD去噪原理框图

2 小波阈值去噪原理

Donobo 和 Johnstone［9］提出了基于小波阈值的去噪方法，其基本原理是小波变换能把信号的能量集中在少数的小波系数上，而高斯白噪声在正交基上的变换仍然是白噪声，且幅度相同.因此，信号的小波系数的值要大于能量分散幅值较小的噪声的小波系数值.所以，在信号去噪时，认为幅值较大的小波系数主要为信号信息，而幅值较小的小波系数被认为是噪声.小波阈值去噪的基本操作如下:首先对含噪信号x(t)做小波变换，对变换后各层的系数设定一个阈值，对大于和小于这一阈值的系数分别进行处理，最后利用处理后的小波系数重构原始信号，得到去噪后信号xf(t).阈值函数包括软阈值函数和硬阈值函数，软阈值函数为

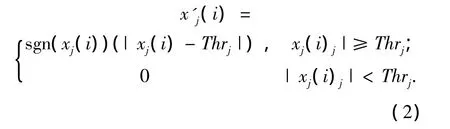
硬阈值函数为

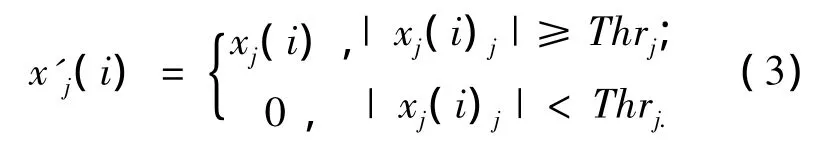
其中:xj(i)为第j层小波分量第i个系数;x'j(i)为经过阈值处理后的第j层小波分量第i个系数.

阈值确定准则包括固定史坦无偏估计(Rigrsure)、自适应史坦无偏估计(Heursure)、极大极小准则(Minimaxi)和固定门限准则(Sqtwolog).从某种意义上说，阈值处理直接决定了信号去噪的质量.因此，阈值的估计和阈值函数的选取成为阈值去噪方法的一大难点和重点.大量研究［10］表明，小波阈值去噪方法适用于高信噪比的信号去噪.

3 EMD及小波分解结合去噪原理

由于EMD去噪和小波阈值去噪各有优缺点，因此本文研究将二者结合起来的方法，以充分发挥各自优点.将EMD去噪和小波阈值去噪结合起来主要有3种方式:1)对信号进行EMD分解后，对得到的每IMF分量和残余项利用小波阈值进行去噪.本文称之为IMF-Wavelet方法.2)先对信号进行EMD去噪，然后再对去噪后信号进行小波阈值去噪，本文称之为EMD-Wavelet方法.3)先对信号进行小波阈值去噪，然后再对去噪后信号进行EMD去噪，本文称之为Wavelet-EMD方法.

4 仿真实验及分析

为了验证本文随提方法的有效性，并且选择最合理的结合方法，利用去噪算法分析的标准信号和在直升机常用碳纤维材料试件上的断铅模拟声发射信号进行仿真分析.采样信噪比(RSN)来评估算法的性能.

4.1 标准信号去噪实验

利用Matlab中的wnoise函数生成具有不同信噪比，长度为 2 048的“Blocks”，“Bumps”，“Heavy sine”和“Doppler”4类具有典型特征的测试信号.图2为“SQRT－”信噪比为2 dB时生成的4类含噪信号波形.图3为利用IMF-Wavelet方法对4类含噪信号去噪后的波形，图4为利用EMD-Wavelet方法对4类含噪信号去噪后的波形，图5为利用Wavelet-EMD方法对4类含噪信号去噪后的波形.其中3种方法中，小波基函数都选用db10小波函数，并且都进行3层分解，采用软阈值方法，阈值采用自适应史坦无偏估计得到.

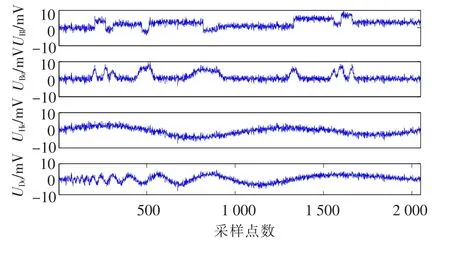
图2 用wnoise产生的含噪信号

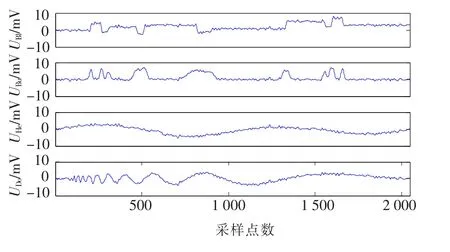
图3 用IMF-Wavelet方法去噪结果

为了进一步验证本文所提方法的有效性，生成了不同信噪比的4类含噪信号，对直接小波去噪，直接 EMD去噪，IMF-Wavelet去噪，EMDWavelet去噪和Wavelet-EMD去噪性能进行了比较.其中小波基函数都选用db10小波函数，并且都进行3层分解，采用软阈值方法，阈值采用自适应史坦无偏估计得到.

通过比较可以看出，小波阈值去噪适合于信噪比较高的情况，本文所提出的EMD和Wavelet结合的3种方法中，Wavelet-EMD方法无论在高信噪比情况下，还是在低信噪比情况下，都具有较稳定的去噪效果，特别是在低信噪比情况下，仍然能够有效地去除噪声.

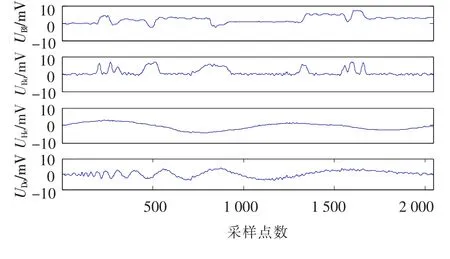
图4 用EMD－Wavelet方法去噪结果

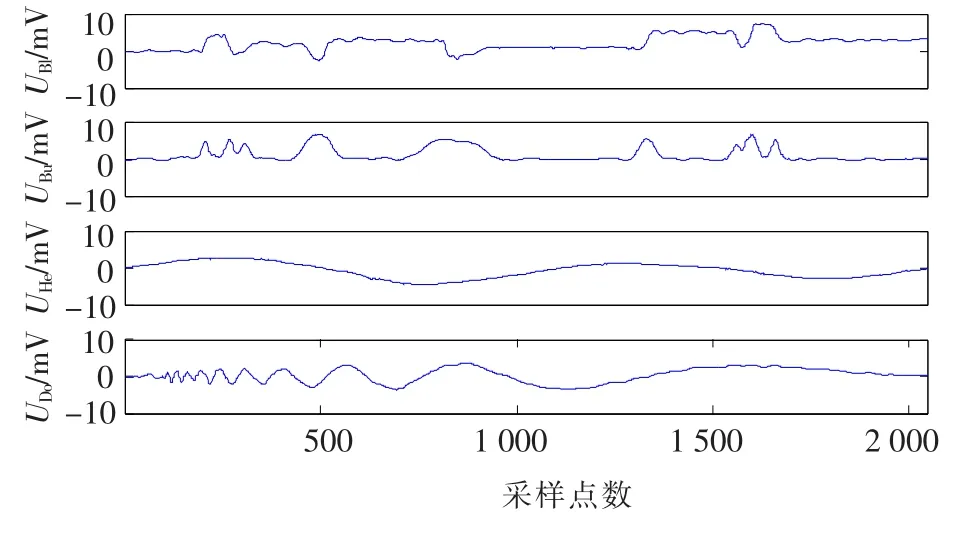
图5 用Wavelet-EMD方法去噪结果

4.2 断铅模拟AE信号去噪实验

为了验证本文所提方法对于声发射信号的去噪效果，在直升机常用的碳纤维材料试件上进行断铅试验，模拟声发射信号，然后对其叠加不同强度的高斯白噪声，对直接小波去噪，直接EMD去噪，IMF-Wavelet去噪，EMD-Wavelet去噪和 Wavelet-EMD去噪性能进行比较.图6为对信噪比为4.309 2的断铅AE信号去噪结果，其中S代表含噪信号，IW代表IMF-Wavelet去噪信号，EW代表EMD-Wavelet去噪信号，WE代表 Wavelet-EMD去噪信号，W代表直接小波去噪信号，E代表直接EMD去噪信号，图7为对信噪比为－1.808 3的断铅AE信号去噪结果，可以明显看出直接小波去噪方法效果较差，EMD-Wavelet和 Wavelet-EMD去噪方法效果最好.

通过比较可以看出，直接小波阈值去噪对于声发射信号去噪效果不是很明显，特别是在信噪比较低的情况下更为明显.本文所提方法EMDWavelet和Wavelet-EMD方法对于含噪声发射信号去噪效果均优于直接小波阈值去噪，直接EMD去噪和IMF-Wavelet去噪算法，并且Wavelet-EMD方法的性能略优于EMD-Wavelet方法，因此在声发射信号去噪中建议采用Wavelet-EMD去噪方法.

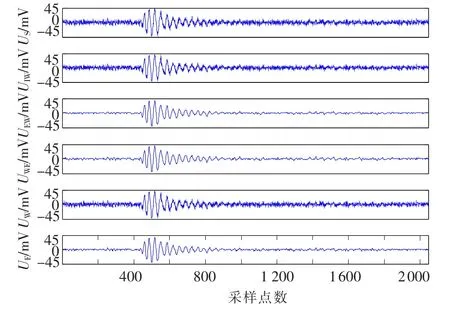
图6 断铅AE信号去噪结果

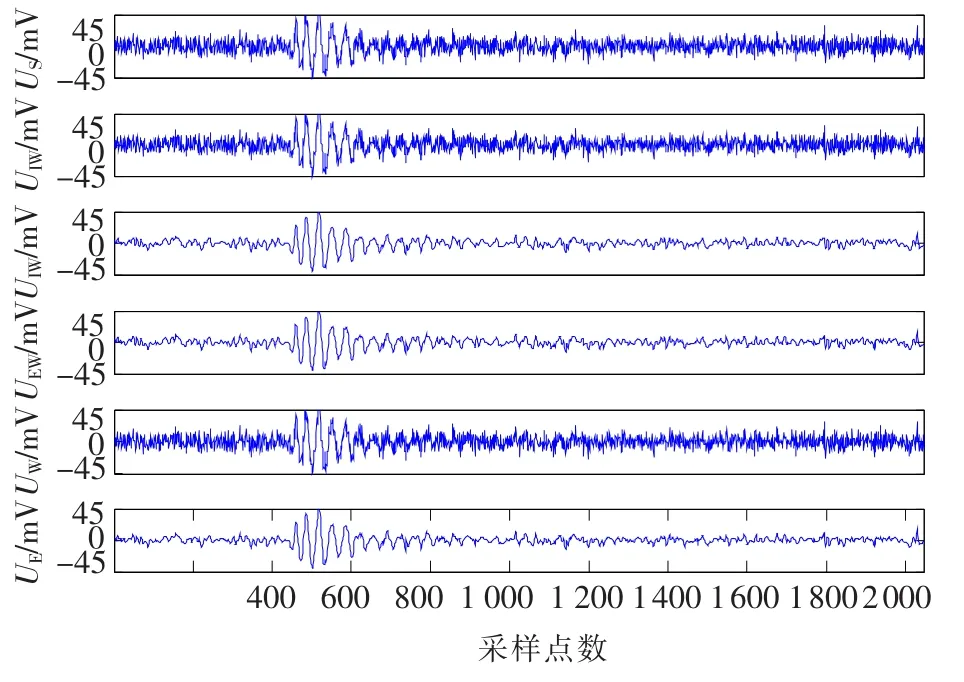
图7 断铅AE信号去噪结果

5 结论

1)将EMD去噪方法和小波阈值去噪方法结合起来，提出了 IMF-Wavelet去噪方法，EMDWavelet去噪方法和Wavelet-EMD去噪方法，小波阈值去噪在信噪比较低的情况下，性能急剧下降，Wavelet-EMD方法无论在高信噪比情况下，还是在低信噪比情况下，都具有较稳定的去噪效果.

2)利用标准信号和断铅模拟声发射信号对算法性能进行分析，直接小波阈值去噪对于声发射信号去噪效果不是很明显，EMD-Wavelet和Wavelet-EMD方法对于声发射信号去噪效果较稳定.

［1］耿荣生，沈功田，刘时风.声发射信号处理和分析技术［J］.无损检测，2002，24(1):23－28.

［2］唐世伟，林君.小波变换与中值滤波相结合图像去噪方法［J］.哈尔滨工业大学学报，2002，24(1):1334－1336.

［3］SHAO Qunfeng，ZHANG Xiaoping，QIA Xiaoqiong，et al.Optical wavelet de-noising applied in multi-span nonlinear fiber links ［J］.Optics Communications，2010，283(7):1261－1267.

［4］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis ［J］.Proc R Soc Lond A，1998，454:903－995.

［5］BOUDRAA A O，CEXUS J C.EMD-based signal filtering［J］.IEEE Transactions on Instrumentation and Measurement，2007，56(6):2196 －2202.

［6］MANUEL B V，WENG B W，BARNER K E.ECG signal denoising and baseline wander correction based on the empirical mode decomposition［J］.Computers in Biology and Medicine，2008，38(1):1－13.

［7］曲从善，路廷镇，谭营.一种改进型经验模态分解及其在信号消噪中的应用［J］.自动化学报，2010，36(1):67－73.

［8］BOUDRAA A O，CEXUS J C.De-noising via empirical mode decomposition［C］//Proceedings of the IEEE International Symposium on Control Communications and Signal Processing.Marrakech，Morocco:IEEE，2006:4－8.

［9］DONOHO D L.De-noising by soft-thresholding［J］.IEEE Transactions on Information Theory，1995，41(3):613－627.

［10］杜修力，何立志，侯伟.基于经验模态分界(EMD)的小波阈值除噪方法［J］.北京工业大学学报，2007，33(3):265－272.

De-nosing of acoustic emission signals based on empirical mode decomposition and wavelet transform

YU Jin-tao1，2，ZHAO Shu-yan1，WANG Qi1

(1.Department of Automatic Measurement and Control，Harbin Institute of Technology，150001 Harbin，China，hityjt@sina.com;2.School of Computer and Information Engineering，Harbin University of Commerce，150028 Harbin，China)

To solve the acoustic emission(AE)signal de-noising problem，de-noising approaches based on empirical mode decomposition and wavelet transform were proposed，including IMF-Wavelet method，EMDWavelet method and Wavelet-EMD method.The standard noise signals and AE signals by pencil lead break were used to analyze the de-noising performance.The simulation results indicate that for the standard noise signals，Wavelet-EMD method has stable de-noising performance whether in high or low signal to noise ratio(SNR)case.Wavelet threshold method is not suitable for AE signal de-noising，EMD-Wavelet and Wavelet-EMD method have stable de-noising performance for AE signals.

empirical mode decomposition;wavelet transform;threshold;de-nosing;acoustic emission

TG115;O3271

A

0367－6234(2011)10－0088－05

2011－07－05.

国家自然科学基金资助项目(60901042);黑龙江省自然科学基金资助项目(F201018).

于金涛(1974—)，男，副教授，博士研究生;

王 祁(1944—)，男，教授，博士生导师.

(编辑 魏希柱)