大跨度拱桥中钢管混凝土应用的探讨

侯志伟

(保定市交通局公路勘测设计院)

大跨度拱桥中钢管混凝土应用的探讨

侯志伟

(保定市交通局公路勘测设计院)

介绍了钢管混凝土的几种计算方法，可以根据不同的阶段采用合适的计算理论，但前三种方法都是钢筋混凝土的计算理论，结合目前国内的钢管混凝土三大理论体系及规范对钢管混凝土的力学性能进行了简单介绍;还简单介绍了钢管混凝土在拱桥应用时稳定问题的有限元分析理论。

大跨度;拱桥;钢管混凝土

1 概述

在最近的50多年里，国内外众多的学者采用各种研究方法和手段，对钢管混凝土的基本理论进行了大量的研究，取得了丰硕的研究成果。

在不同的施工状态下，钢管混凝土拱桥截面几何特性的合理计算有待于探讨。目前在计算钢管混凝土拱桥的几何特性时，一般采用如下方法。

(1)换算截面法：将混凝土面积按一定原则换算为钢管的面积，从而将钢管混凝土视为单一材料。钢管混凝土构件弹性模量采用钢管弹性模量Es

组合面积为

抗弯刚度为

抗扭刚度为

其中

E为弹性模量;G为剪切模量;I为惯性矩;Ip为扭转惯性矩;A为截面积;下标s表示钢材;下标c表示混凝土。

(2)双单元法：将钢管混凝土中的钢管与混凝土分别用不同的单元来模拟，保证其节点坐标相同，分别按各自的截面面积、抗弯刚度进行计算。

(3)组合单元法：将钢管混凝土中的钢管与混凝土合成一个单元。

对钢管混凝土受压构件采用另外一种表达方式计算。

以上三种计算方法都是采用的钢筋混凝土的计算理论，没有考虑钢管的套箍作用。

(4)统一理论法：将钢管和混凝土作为一种新的组合性材料，在其力学和物理指标中予以体现。

钢管混凝土作为一种复合材料是在钢管内填充混凝土，其工作性能较单一材料有较大提高。钢管的套箍作用大大提高了混凝土的塑性性能，使得混凝土，特别是高强混凝土的脆性弱点得到克服。因此，钢管混凝土材料应用于以受压为主的构件中，较之钢结构和混凝土结构有着极大的优越性。

(1)轴心受压构件的基本工作性能

钢管混凝土材料主要用于受压结构，轴心受压时其受力机理分为三个阶段，即：弹性工作阶段、弹塑性工作阶段、强化阶段。

①含钢率很低时(ρ＜4%或D/t＞100)，钢管对混凝土的产生的侧压力很小。

②含钢率较低时(ρ为5% ～6%或D/t＜67～80)，曲线由三段组成。

③含钢率较高时(ρ为6% ～7%或D/t＜57～67)，曲线由三段组成。

对于含钢率较高的第三类型构件，与钢结构类似有明显的强化作用。对轴心受压的钢管混凝土短柱，N-ε曲线几乎不下降，有些试验还出现压不坏的现象。

(2)轴心受压构件的强度计算

我国自20世纪50年代开始对钢管混凝土的基本理论进行了大量的研究，取得了可喜的成果，大致形成了三个理论体系。

中国工程技术标准化协会标准《钢管混凝土结构设计与施工规程》，国家建材工业局颁布的《钢管混凝土结构设计与施工规程》，能源部颁布的《钢-混凝土组合结构设计规程》，该规程所依据的基本理论视钢管混凝土为一种材料，采用统一理论，以建立在试验基础上的理论公式为主，在公式形式方面更多的借鉴了钢结构的设计理论，对压弯构件采用应力表达方式，而不是承载力，由于公式较繁，更多地采用了表格的形式，因此实际应用时受到应用表格范围的限制。

(3)偏心受压构件承载力的计算

钢管混凝土压弯构件，一开始受力就存在着挠曲，截面上的应力分布不均匀。判断构件是否强度破坏取决于其长细比。

极值点破坏的荷载挠度曲线由上升段和下降段组成，分界点就是极值点。由于构件的不同长细比和荷载相对偏心率的不同，危险截面上应力的分布有三种情况。

2 钢管混凝土拱桥的稳定分析

桥梁失稳事故的发生促使了桥梁稳定理论的发展。1988年恩格塞(Engesser)建议用切线模量Et代替欧拉公式中的弹性模量E来计算临界荷载。

恩格塞以康西特尔的概念为基础导出了有效模量的一般公式，即双模量公式。1910年卡门(Karman)独立地重新导出了双模量理论，并进行了一系列的实验去校核这一理论的正确性。证明其临界荷载值大大低于欧拉理论的临界值，同时又不能用分支点的概念来解释。因而引入了极值点失稳的观点以及跳跃现象的稳定理论。

研究表明，只有通过对结构几何非线性关系以及材料非线性本构关系的研究，才能深入揭示复杂稳定问题的实质。

2.1 线弹性稳定的基本理论

线弹性稳定的有限元平衡方程为

其中：KD为单元几何刚度矩阵;KG为通常的单元弹性刚度矩阵。

解此线性代数方程组即可求出节点位移{d}，然后再求出杆件的内力。

对结构进行稳定分析，关心的就是结构的稳定系数lcr。因为几何刚度矩阵KD由轴力决定，故可以知道此时的几何刚度矩阵为lcrKG，由(1)可得

对于处在随遇平衡状态的结构，即使再给一个微小的位移扰动D{d}，(2)的平衡方程仍然成立，即

而能够同时使(2.19)和(2.20)成立的条件为：

(［KD］+lcr［KG］)D{d}={0}这就是计算稳定安全系数的特征方程，如果方程有n阶，那么在理论上存在n个特征值{l}={l1，l2，…，ln}。

这就是计算稳定安全系数的特征方程，即

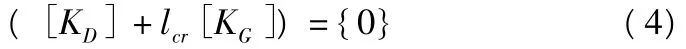
对于通常的桥梁结构，直接求解(2.4)的特征值相当困难，通常采用迭代法求解，其迭代格式为

2.2 考虑几何非线性的稳定基本理论

结构在荷载{F}作用下有一定的变形，严格来说，结构的几何参数这样带来的计算误差较大，就不能满足工程问题的要求，这就成为几何非线性问题即通常所说的大变形或大挠度理论。

由虚位移原理有：外力因虚位移所做的功等于结构因虚位移应变所产生的应变能。即

初始应力矩阵或几何刚度矩阵。由下式给出

òd［BL］T{s}dv=［Ks］{d} 式中{d}由(2.26)给出。

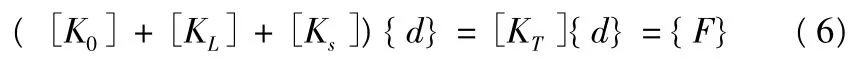
于是，考虑几何非线性的有限元一般平衡方程可以用下式写出其中：［KT］=［K0］+［KL］+［Ks］称为考虑几何非线性的切线刚度矩阵。

这种算法在每一次迭代时都要不断地修正刚度矩阵，很费机时，不利于编制计算机程序。

2.3 虑材料非线性的稳定基本理论

材料非线性的基本假定：

(1)加载过程中平截面假定始终成立。

(2)忽略剪应力和剪应变的影响。

(3)钢管和混凝土之间无纵向滑移，在环向变形协调。

2.4 双重非线性的稳定基本理论

对于大跨径钢管混凝土拱桥不可避免地需要进行同时考虑结构材料、几何非线性的双重非线性的分析。将荷载分成许多等级，由程序自动计算荷载增量步长，各级荷载增量也可以不等，在各级荷载之间考虑材料非线性，在每一级荷载内部由迭代法考虑几何非线性，这是比较理想的。

［1］叶列平，方鄂华.钢骨混凝土构件的受力性能研究综述［J］.土木工程学报，2000.

［2］肖季秋等.劲性钢筋混凝土粘结性能的试验研究.四川建筑科学研究院，1992.

［3］过镇海.钢筋混凝土原理［M］.清华大学出版社，1999.

［4］项海帆.高等桥梁结构理论［M］.北京：人民交通出版社，2000.

U445

C

1008-3383(2011)09-0254-02

2011-06-26

侯志伟(1973-)，女，河北定州人，工程师，主要从事公路及桥梁工程勘察设计工作。