自适应干扰对消系统中的积分控制与低通控制

蒋云昊 潘启军 唐 健 李 毅

（1.华中科技大学电气与电子工程学院 武汉 430074

2.海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033）

1 引言

从混有噪声的信号中提取有用信号通常是设计滤波器。如果按照某种准则，使设计的滤波器在该准则下最优，这就是最优滤波问题。随着自适应概念的出现，人们又对自适应滤波给以极大的兴趣，其中很重要的一个应用领域就是自适应噪声对消。B.Widrow等早先对自适应噪声对消进行了研究，并提出如今广泛应用的LMS算法[1]。只要能从噪声场中获得参考输入，就能将该噪声从信号中衰减或滤除以获得有用信号。J.Glover从频域研究了正弦信号下的自适应噪声对消技术[2]，随后人们对LMS算法的统计性能和改进算法进行了大量的研究[3-9]，并将自适应噪声对消技术应用到干扰抑制和噪声控制等方面[10-14]。Compton从统计分析的角度对自适应阵列中积分器极点对系统性能的影响进行了理论分析[15]。

本文针对共平台接收机受到临近发射机的阻塞式干扰的突出问题进行研究，采用自适应干扰对消技术来抑制干扰。研究的干扰信号为窄带信号，载波频率在2MHz至数十MHz，因此从实际器件速率和信号特性考虑，以模拟电路实现的单频干扰信号的分析作为系统设计的参考。

有关LMS算法的数字理论研究较多，大多从统计信号理论进行分析。LMS算法权值更新从模拟实现的角度需要理想积分器，而实际器件无法实现真正的积分，通常用低通近似积分，带来的问题就是权值不会收敛到最优。本文针对研究对象的特点，从低通控制的角度研究系统的时域特性，并和通常低通控制忽略高频项的分析方法进行比较，得出一些有益结论。为了和理想的积分控制下系统的特性比较，首先对积分控制进行分析。

2 系统模型

自适应干扰对消系统如图1所示，图中XI（t）为干扰信号，Xε（t）为误差信号，相互正交的参考信号为Xs1（t）和Xs2（t），W1（t）和W2（t）为权值，Y1（t）和Y2（t）为加权输出信号，Y（t）为加权输出合成信号，k为权值支路增益。

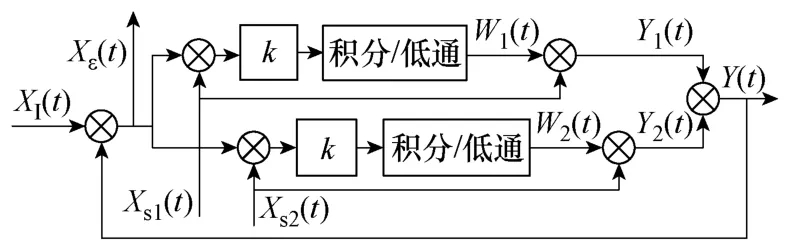
图1 自适应干扰对消系统Fig.1 The adaptive interference cancellation system

假设参考信号为

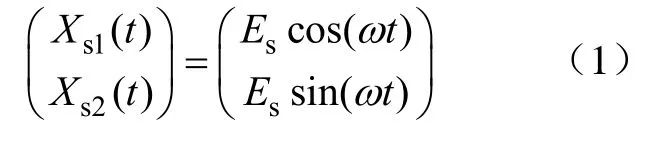
干扰信号为

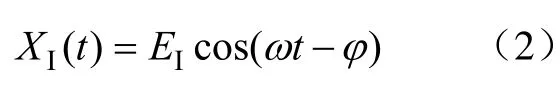
剩余误差为

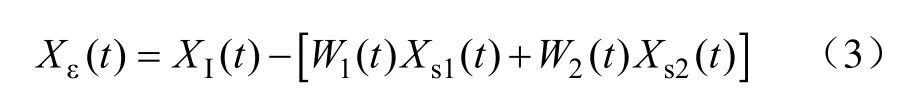
式中φ—干扰信号初相位；

ω—信号角频率；

Es—参考信号的幅值；

EI—干扰信号的幅值。

3 信号乘积与相关性

参考信号和误差信号的乘积为

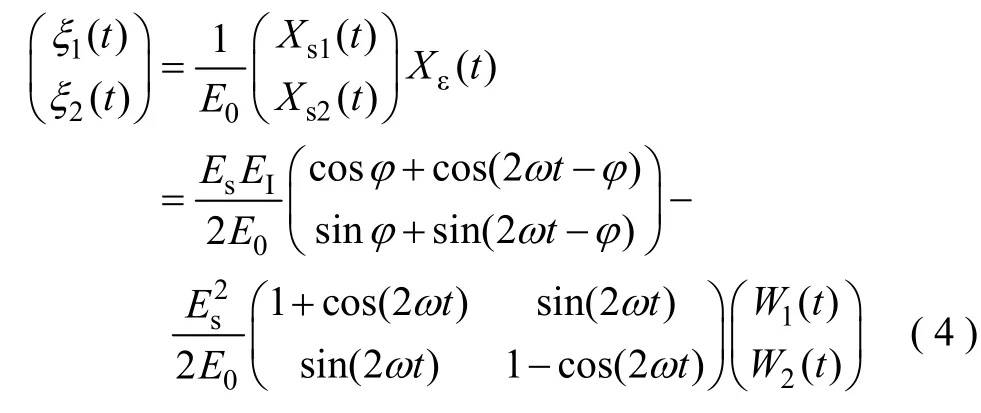
参考信号和误差信号的相关性为

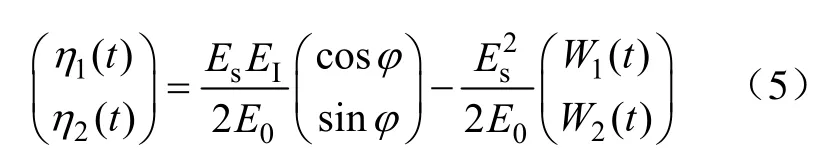
式中，E0为乘法器的标准信号。

由式（5），当相关性为零时，可得系统的最优权值为

4 积分控制时域分析

根据图1，积分的传递函数表达式为1/(τs)，其中τ为时间常数。可得权值微分方程组为

将式（4）代入式（7），可得

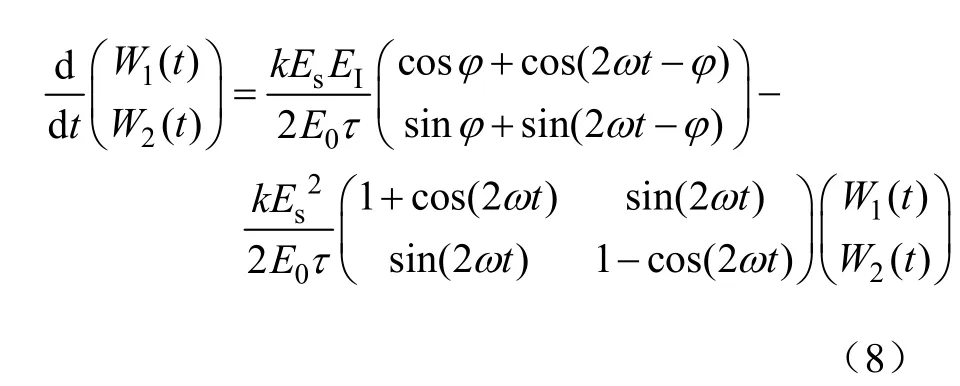
式（8）为周期时变微分方程组，取权值系数矩阵的特征矢量构造变换矩阵

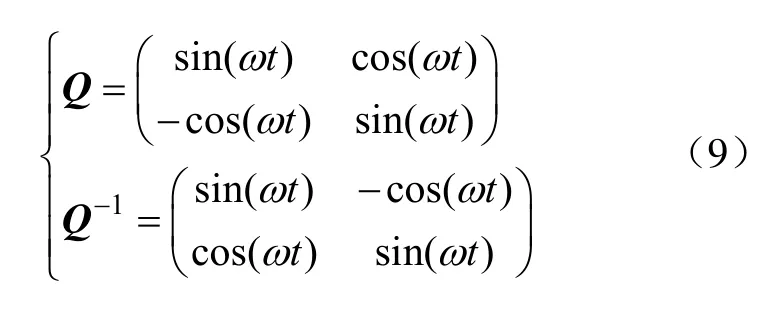
满足

式中，0和2为系数矩阵的特征根。

令

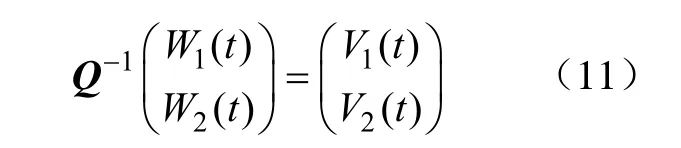
权值微分方程组可化为

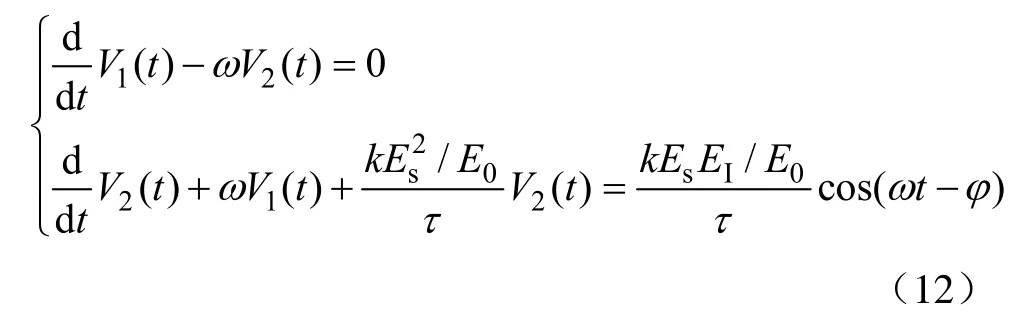
求解式（12）的特征根为

由式（13）可见，系统是稳定的。

式（12）的特解为

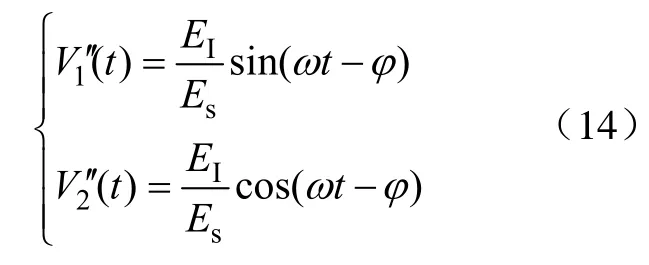
利用式（11）可得自适应干扰对消系统的稳态权值为

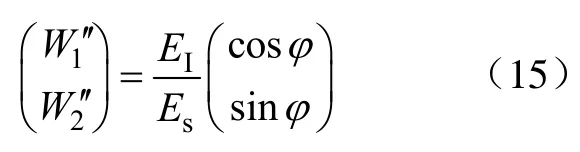
可见，积分控制下系统的稳态权值就是使干扰对消至零的最优权值。

下面将讨论V1（t）和V2（t）在三种阻尼特性下，系统权值和误差的收敛过程。

4.1 过阻尼

V1（t）和V2（t）工作在过阻尼状态的条件为

可求得V1（t）和V2（t）的解为

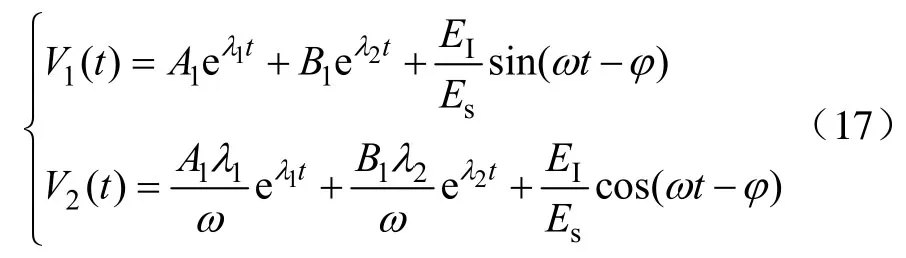
式中，A1、B1为待定常数。

由式（11）反变换可得此时系统的权值解为

由式（3）可得此时系统误差的收敛过程为

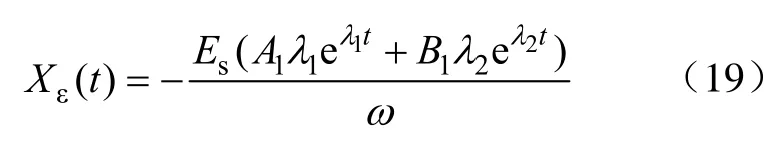
4.2 临界阻尼

V1（t）和V2（t）工作在临界阻尼状态的条件为

可求得此时系统的权值解为

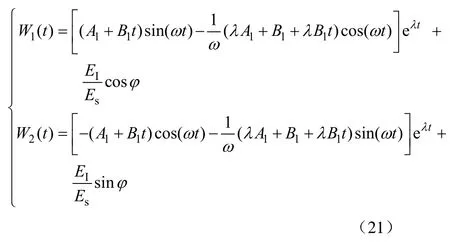
式中，A1、B1为待定常数。

由式（3），此时系统误差的收敛过程为

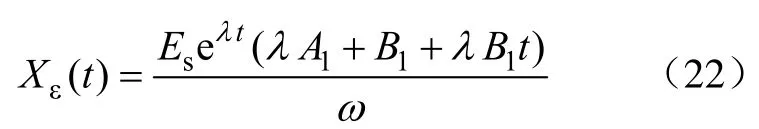
4.3 欠阻尼

V1（t）和V2（t）工作在过阻尼状态的条件为

此时系统的特征根可表示为

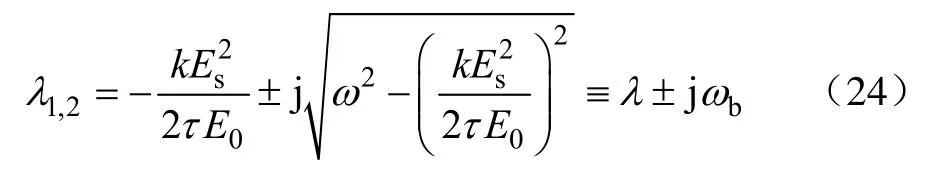
可求得此时系统的权值解为

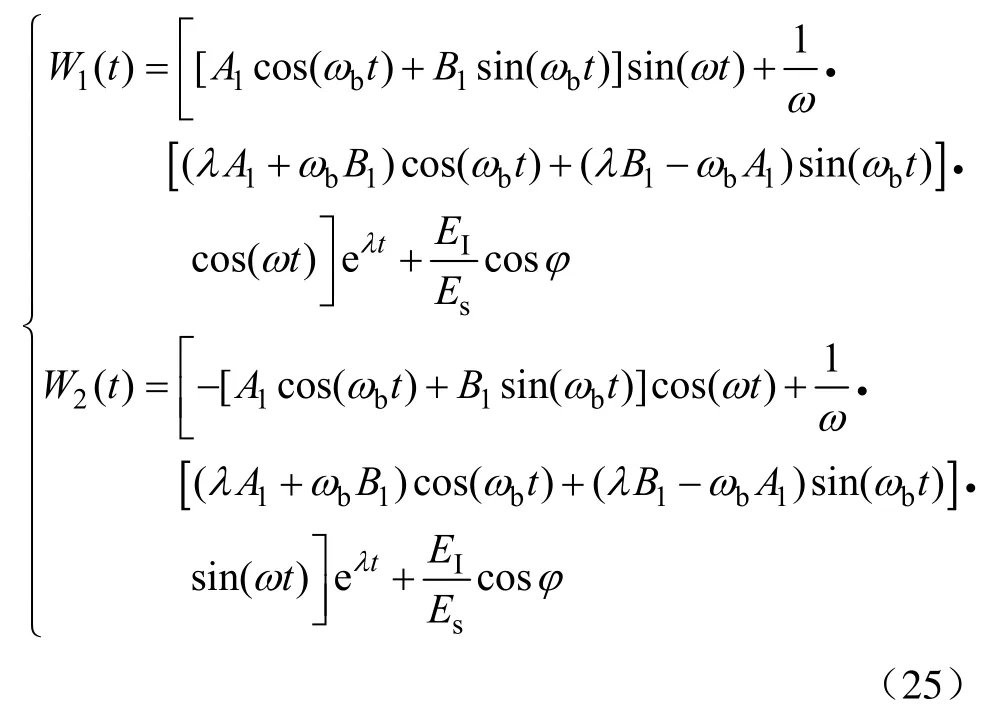
式中，A1、B1为待定常数。

由式（3）可得此时系统误差的收敛过程为

由以上三种情况的权值收敛过程可见，稳态后的权值就是系统的最优权值，并由误差收敛过程可见系统的稳态误差为零。

当系统工作在临界阻尼时，有最快的收敛速度。所以设计时，对系统参数的选择要尽量使系统工作在临界阻尼附近，以获得综合的最佳效果。

5 低通控制时域分析

如图1所示，低通的传函表达式为（τ2/τ1）/（τ2s+1），可得权值的微分方程组为

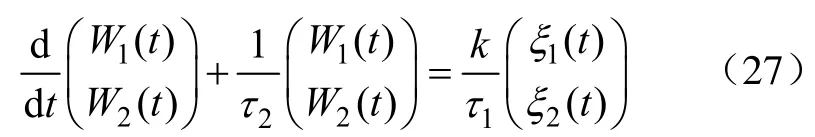
式中，τ1和τ2为有源低通的两个时间常数。式（4）代入式（27）可得

由于权值系数矩阵与式（8）一样，采用同样的变换方法可得常系数微分方程组为

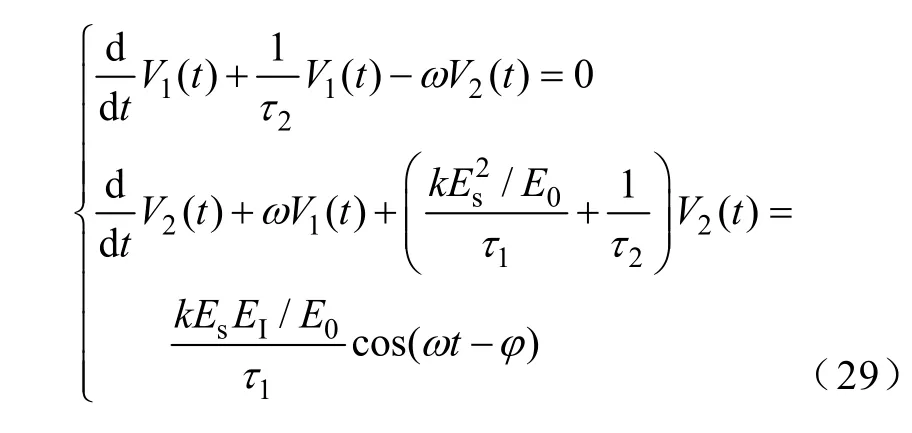
特征根为

由式（30）可见，系统是稳定的。与积分控制的特征根比较可见，若τ1=τ，其他条件相同，则低通控制有比积分控制更快的收敛速度。

5.1 权值和误差的暂态解

根据式（30）可得不同阻尼特性下V1（t）和V2（t）的暂态解，经过反变换可求得权值以及误差的暂态解。不同阻尼情况的条件与积分控制的一样，只是将τ换成τ1。

5.1.1 过阻尼

可求得权值暂态解为

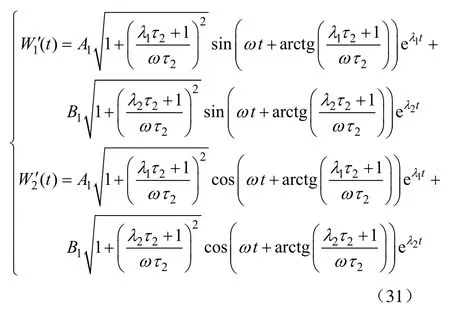
式中，A1、B1为待定常数。

误差的暂态过程为

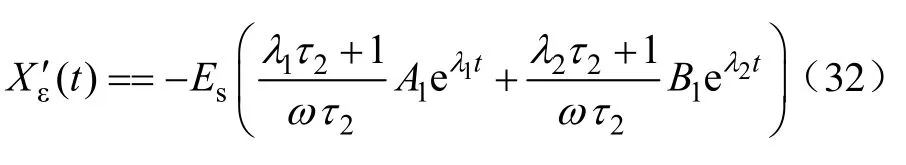
5.1.2 临界阻尼

可求得权值暂态解为

式中，A1、B1为待定常数。

误差的暂态过程为

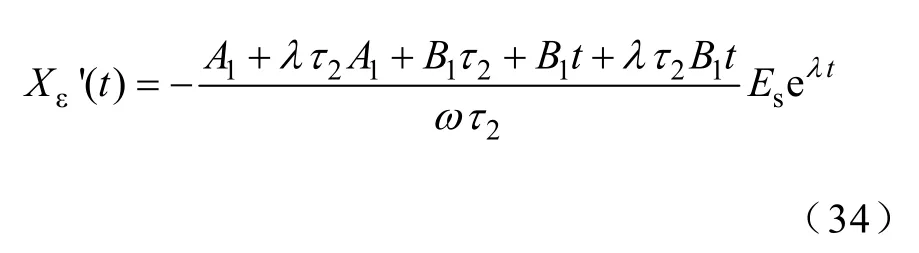
5.1.3 欠阻尼

此时系统的特征根可表示为

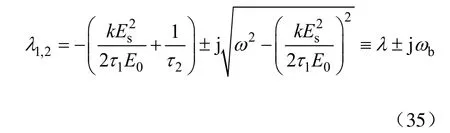
可求得权值暂态解为

式中，A1、B1为待定常数。

误差的暂态过程为

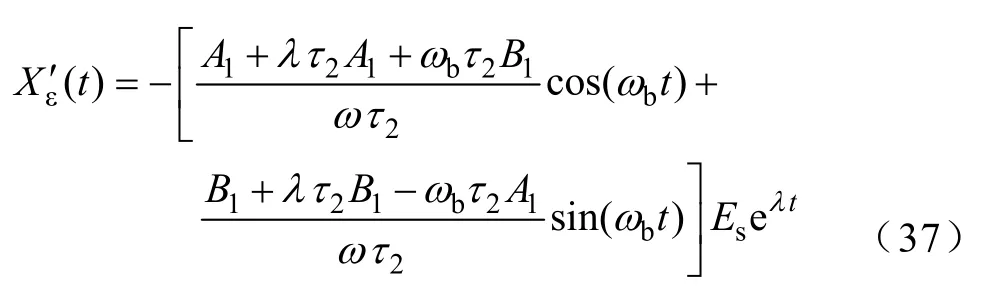
与积分控制一样，当系统工作在临界阻尼时，有最快的收敛速度。所以设计时，对系统参数的选择要尽量使系统工作在临界阻尼附近，以获得综合的最佳效果。

5.2 权值和误差的稳态解

由式（29）可得V1（t）和V2（t）的稳态解，利用式（11）和式（3）可求得系统的权值稳态解和稳态误差。

权值的暂态解为

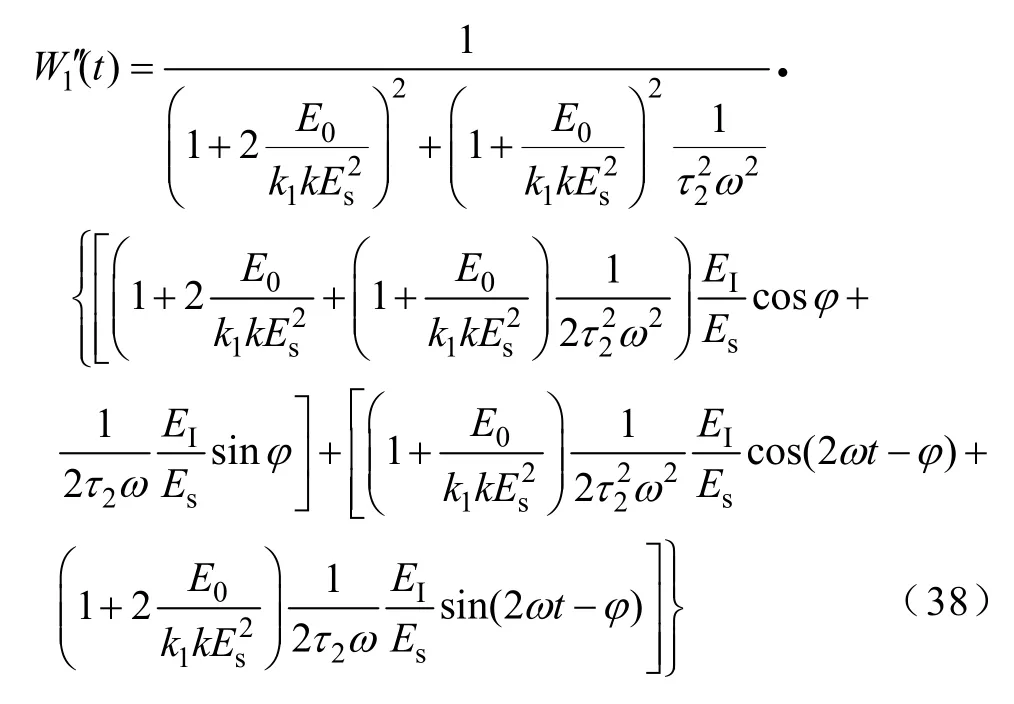
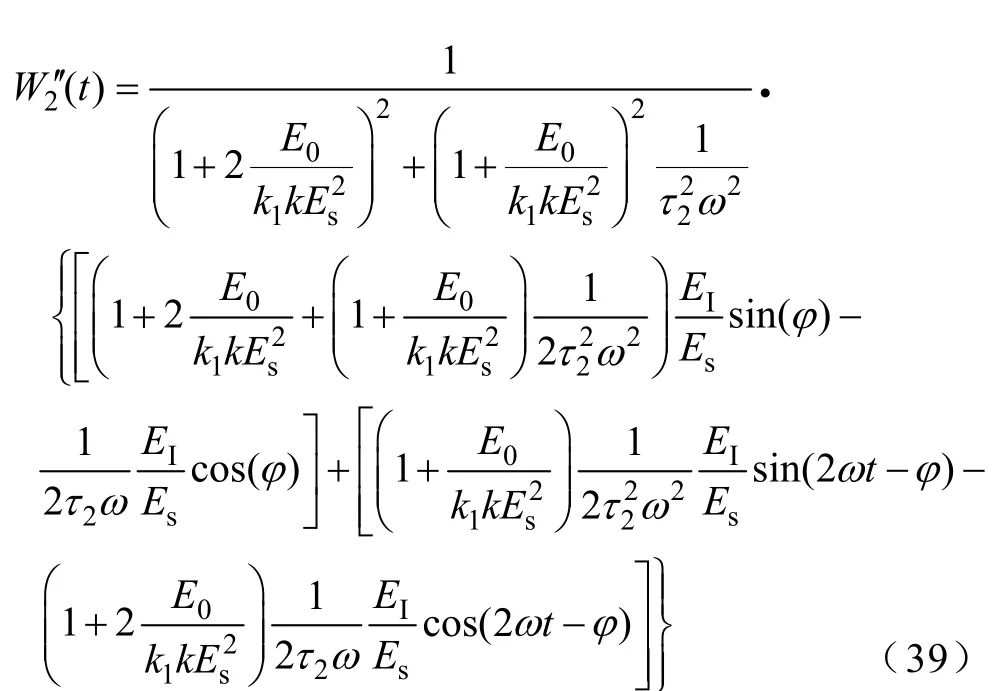
稳态误差为

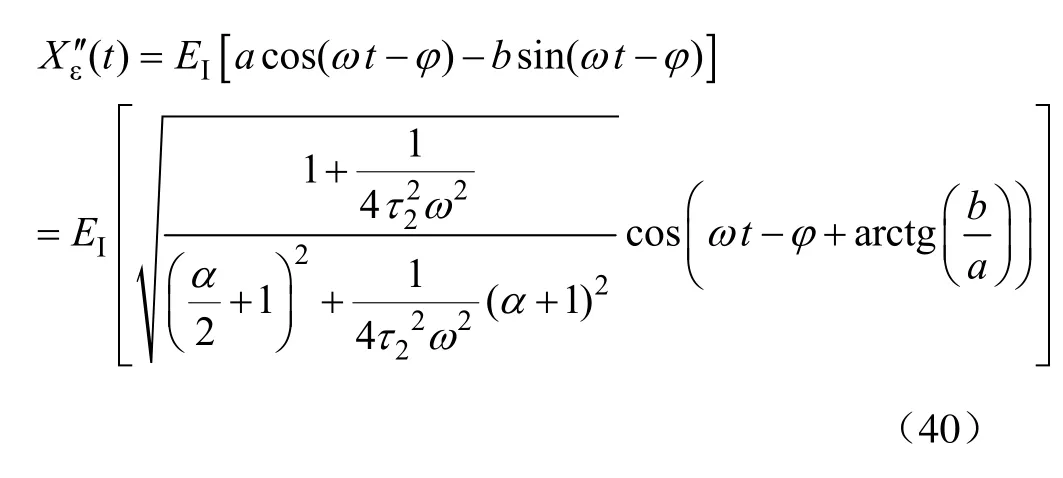
式中

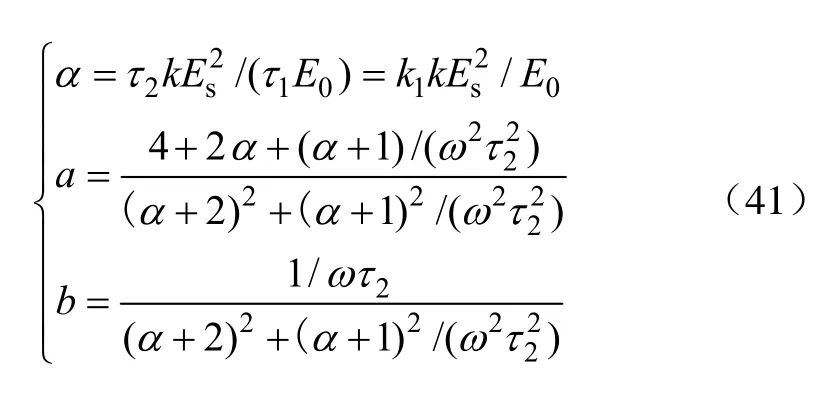
由式（40）可得干扰对消比为

当干扰信号频率较高，满足ωτ2≫1时，若忽略频率项，由式（40）可得

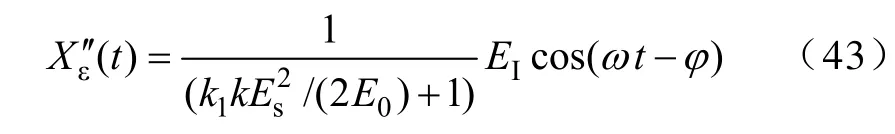
此时的干扰对消比为

由式（38）～式（40）可见，低通控制下，系统的稳态权值已不是式（6）的最优权值，所以稳态误差不为零。当干扰信号的频率较高，忽略该频率项时，系统的稳态权值为

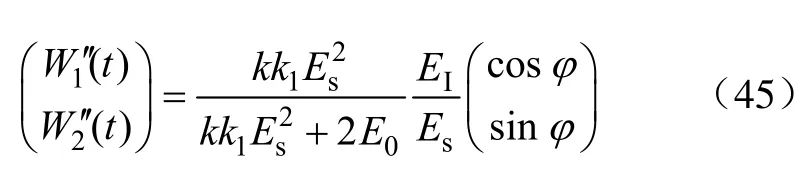
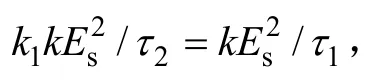
5.3 有用信号权值和误差的稳态解

图1输入端含有用信号时，系统的暂态特性不变。设有用信号为

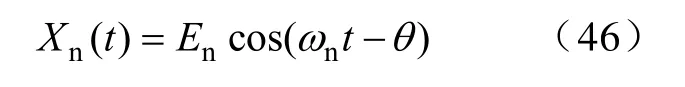
式中En—有用信号的幅值；

θ—有用信号初相位；

ωn—有用信号角频率。

采用与5.1和5.2同样的方法可得稳态权值为

式中

有用信号稳态值为

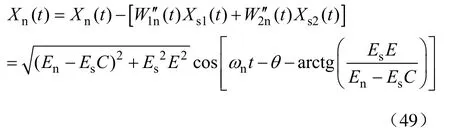
系统对有用信号的对消比为

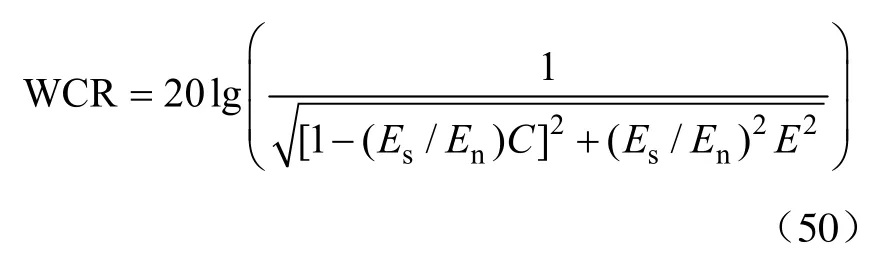
6 算例分析

采用提高增益k和调节τ2的方法进行比较。算例参数设为：En=0.1V，Es=2V，EI=0.2V，E0=1V，τ1=10-4s，ω=2π×2×106rad/s，ωn=(2π×2×106-2×105)rad/s，φ=30°，θ=60°。当τ2=10-4s，k=10～100时，精确计算的干扰对消比ICR1、忽略高频计算的干扰对消比ICR2以及系统对有用信号的对消比WCR随增益k变化的曲线如图2所示。由图2可见，由于干扰信号频率较高，精确计算和忽略高频计算的结果非常接近。而通过增大k提高干扰对消比的同时，对有用信号的衰减也会同样增加。

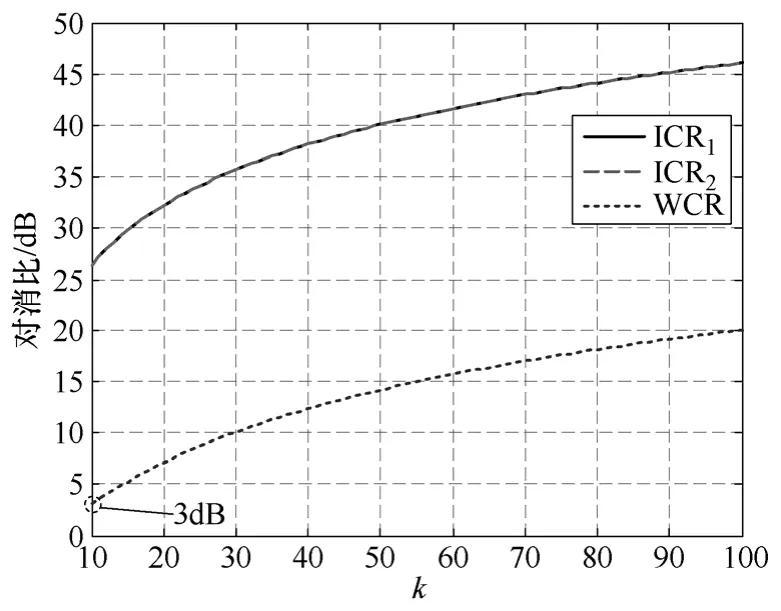
图2 干扰信号和有用信号的对消比随k变化的曲线Fig.2 The cancellation ratio of interference signal and desired signal variation with k

图3 和图4为τ2=10-4s，k=10和k=100时精确计算和忽略高频计算的剩余干扰信号以及剩余有用信号的稳态时域波形。其中的剩余干扰信号为精确计算和忽略高频计算的结果，两者的曲线几乎完全重合。k=100时的剩余干扰信号和剩余有用信号均比k=40时的减小。计算可得k=100时的干扰对消比和有用信号对消比约为46dB和20dB；k=40时的干扰对消比和有用信号对消比约为26dB和3dB，与图2相同条件下的结果一致。

当k=10，τ2=（10-4～10-3）s时，精确计算的干扰对消比ICR1、忽略高频计算的干扰对消比ICR2以及系统对有用信号的对消比WCR随增益k变化的曲线如图5所示，由图可见，精确计算和忽略高频计算的结果非常接近。在干扰对消比提高的同时，有用信号的衰减没有变化。

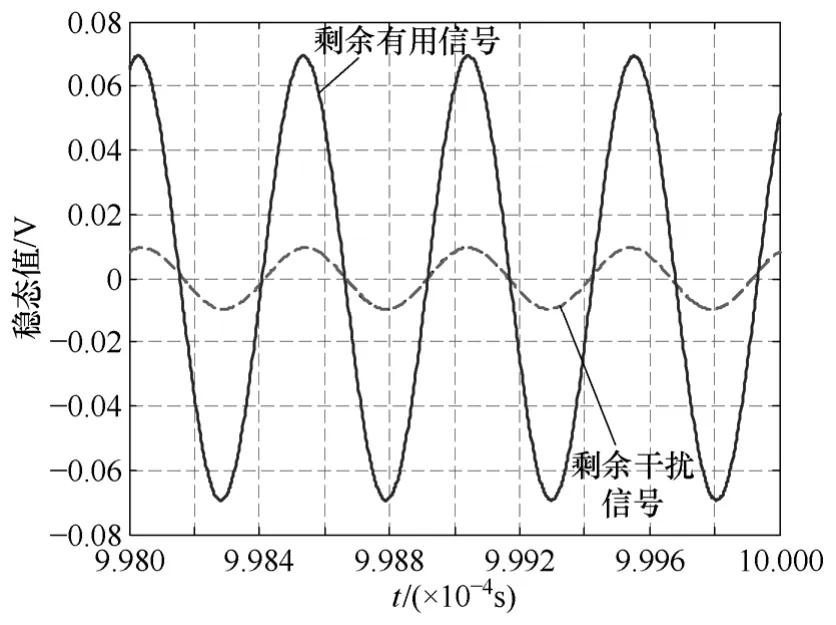
图3 剩余干扰信号和剩余有用信号的时域波形(k=10)Fig.3 The waveforms of residual interference signal and residual desired signal(k=10)

图4 剩余干扰信号和剩余有用信号的时域波形（k=100）Fig.4 The waveforms of residual interference signal and residual desired signal（k=100）

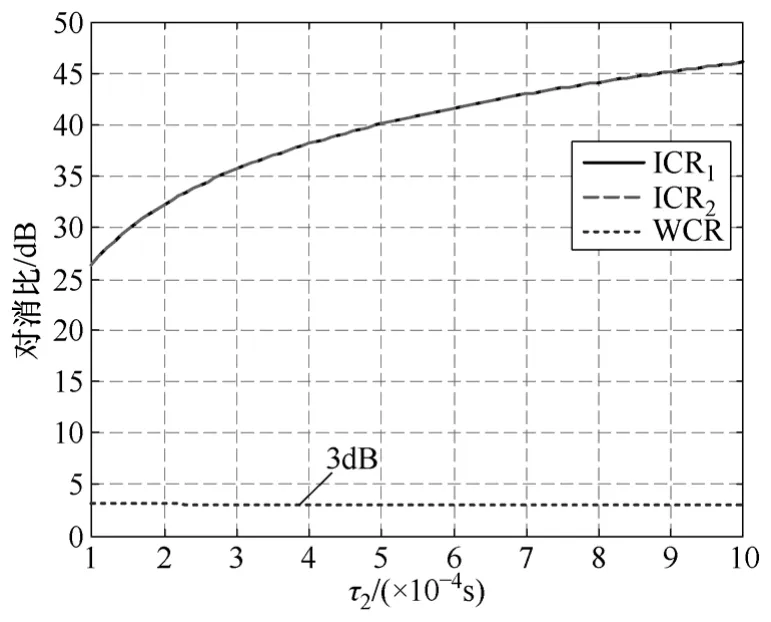
图5 干扰信号和有用信号的对消比随τ2变化的曲线Fig.5 The cancellation ratio of interference signal and desired signal variation with τ2

图6 为k=10，τ2=10-3时的剩余干扰信号和剩余误差信号的时域波形，其中剩余干扰信号为精确计算和忽略高频计算的结果，两者曲线几乎完全重合。比较图6和图3可见，τ2增大使剩余干扰信号减小，计算可得此时的干扰对消比约为46dB与图5相同条件下的结果一致。而有用信号的衰减没有变化，仍为3dB，与图5的结论一致。

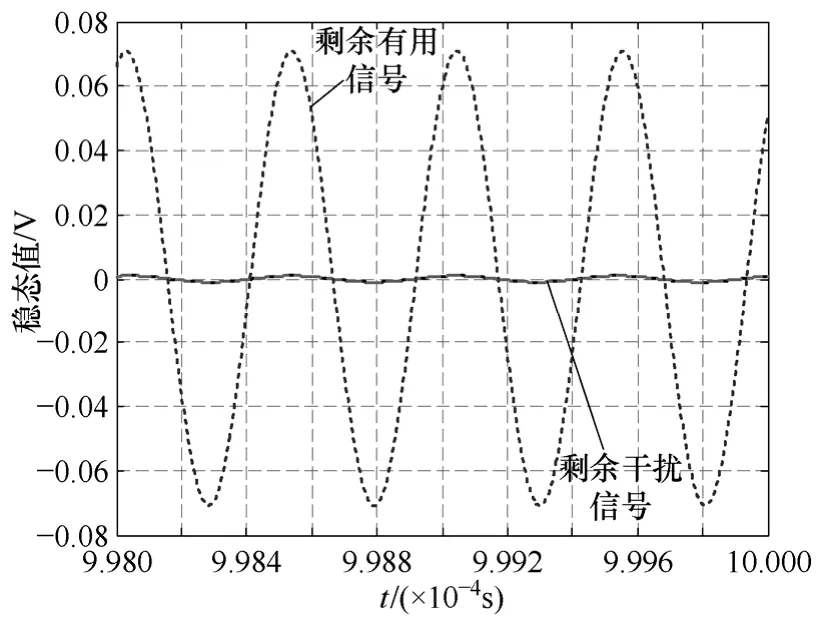
图6 剩余干扰信号和剩余有用信号的时域波形Fig.6 The waveforms of residual interference signal and residual desired signal

7 结论

本文求解了自适应干扰对消系统中采用积分控制和低通控制的权值和误差的解析解，得到以下结论：

（1）通常忽略高频项对系统模型的求解得到的暂态特性是平均意义下的，不能反映系统的不同阻尼特性，对稳态权值和稳态误差以及干扰对消比的计算也是近似的。

（2）当τ2→∞时，低通控制等效为积分控制。仅通过增大k来提高干扰对消比会使系统的3dB带宽随之增大，而通过增大τ2来提高系统的增益和干扰对消比可以保证系统的3dB带宽不变，有利于保证系统的频率选择性。

[1] Widrow B,Glover J R,Cool Mc J M,et al.Adaptive noise cancelling: principles and applications[J].Proceedings of the IEEE,1975,63(12): 1692-1716.

[2] Glover J R.Adaptive noise canceling applied to sinusoidal interferences[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1977,25(6): 484-491.

[3] Widrow B,Kamenetsky M.On the statistical efficiency of the LMS family of adaptive algorithms[C].Proceedings of the International Joint Conference on Neural Networks,2003: 2872-2880.

[4] Flores A,Widrow B.Assessment of the efficiency of the LMS algorithm based on spectral information[C].Conference Record of the 38th Asilomar Conference on Signals,Systems and Computers,2004: 120-124.

[5] Kamenetsky M,Widrow B.A variable leaky LMS adaptive algorithm[C].Conference Record of the 38th Asilomar Conference on Signals,Systems and Computers,2004: 125-128.

[6] Akhtar M T,Abe M,Kawamata M.A new variable step size LMS algorithm-based method for improved online secondary path modeling in active noise control systems[J].IEEE Transactions on Audio,Speech and Language Processing,2006,14(2): 720-726.

[7] Tobias O J,Seara R.On the LMS algorithm with constant and variable leakage factor in a nonlinear environment[J].IEEE Transactions on Signal Processing,2006,54(9): 3448-3458.

[8] Zhang Y G,Chambers J A,Sanei S,et al.A new variable tap-length LMS algorithm to model an exponential decay impulse response [J].IEEE Signal Processing Letters,2007,14(4): 263-266.

[9] 李嘉全,王永.一种新的滤波X-LMS算法研究[J].振动与冲击,2008,27(3): 5-9.Li J Q,Wang Y.Study on filtered X-LMS algorithm[J].Journal of Vibration and Shock,2008,27(3): 5-9.

[10] Wang Z L,Zhang X W.A high performance speech enhancement algorithm based on double-channel adaptive noise cancelling[C].IEEE International Symposium on Microwave,Antenna,Propagation and EMC Technologes for Wireless Communications Proceedings,2005:983-986.

[11] Das D P,Panda G,Kuo S M.New block filtered-X LMS algorithms for active noise control systems[J].IET Signal Processing,2007,1(2): 73-81.

[12] 周峰,李亚超,邢孟道,等.利用改进的LMS算法抑制时变SAR窄带干扰的研究[J].电波科学学报,2007,22(5): 722-727.Zhou F,Li Y C,Qing M D,et al.Time variable narrow band interference suppression for SAR using the algorithm of improved LMS[J].Chinese Journal of Radio Science,2007,22(5): 722-727.

[13] Huang Y F,Hung H L,Wen J.Performance of a novel adaptive multistage full parallel interference canceller for CDMA systems[J].IEEE Transactions on Vehicular Technology,2008,57(3): 1944-1941.

[14] Paschedag J,Lohmann B.Error convergence of the filtered-X LMS algorithm for multiple harmonic excitation[J].IEEE Transactions on Audio,Speech,and Language Processing,2008,16(5): 989-999.

[15] Compton R T.The effect of integrator pole position on the performance of an adaptive array[J].IEEE Transactions on Aerospace and Electronic Systems,1981,17(4): 598-602.