三维边坡稳定性分析的一种适用方法

黄传志，曹永华，杨京方

（中交天津港湾工程研究院有限公司，港口岩土工程技术交通行业重点实验室，天津市港口岩土工程技术重点实验室，天津 300222）

边坡稳定性分析问题是岩土工程中的主要问题之一。无论是人工边坡、还是天然边坡，滑坡的情况均是在三维条件下发生的，因此，三维边坡问题的研究越来越受到重视。相关的研究成果已有许多文献介绍[1-6]。尽管三维稳定分析具有重要意义，但是，有关的稳定分析方法和程序开发方面的工作还远远不能满足实际需要，大部分研究工作都仅限于学术领域，未见实际应用[7]。所有的三维分析程序都存在引入大量假定的缺欠[7]。研究的方法大多是二维问题的条分法推广到三维问题的条柱法。尽管经过多年的发展，但条柱法并未像二维问题的条分法那样成熟，在实际工程中也未普遍应用[8]。可以说这是国内外学者的普遍看法，也是三维边坡稳定性分析研究的基本现状。

很显然，“存在引入大量假定的缺欠”的原因是对三维边坡稳定问题所应当满足的基本方程研究不足。最近，李树奇[9]等人提出了一套对三维边坡稳定问题普遍适用的基本方程，只需要和二维问题一样引入一个假定条件就能获得具体的分析方法；并基于类似二维问题简化Bishop法的假定，得出了一种分析方法。

众所周知，最早建立的边坡稳定性分析方法是二维问题的简单条分法（Fellenius法），这一方法获得了广泛的应用。本文将基于类似二维问题简单条分法的假定，得出三维边坡稳定分析的一种方法，并讨论方法的应用问题。

1 基本方程

众所周知，边坡稳定问题采用屈服条件：

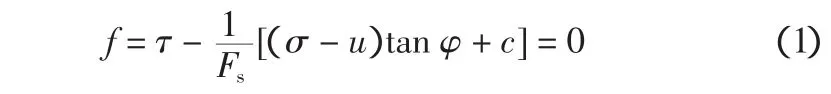
取垂直坐标（z坐标）向下为正，文献 [9]得出以下基本方程。

1.1 曲面上一点的应力关系

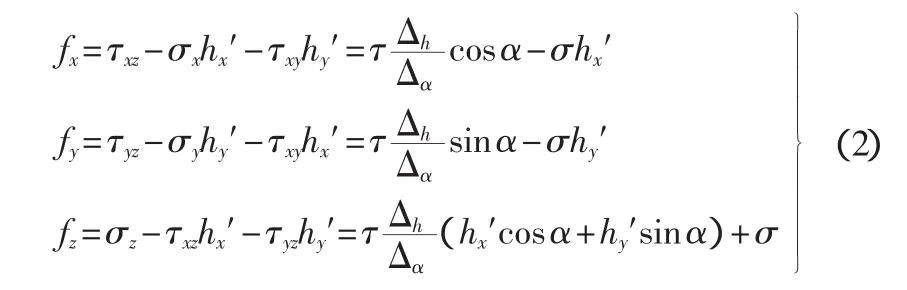
其中：

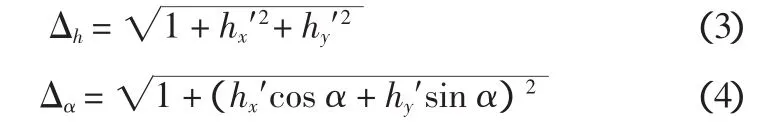
式中：fx、fy、fz分别为平行于坐标轴x、y、z的应力；σx、σy、σz、τxy、τxz、τyz为应力分量；hx′、hy′为空间曲面 z=h（x，y）（可能的滑动面） 的一阶偏导数；σ、τ分别为法向应力、剪应力；α为由剪应力的方向余弦引出，是剪应力在水平面上投影与x坐标轴的夹角，也是滑动面上任意一点的水平破坏方向的方向角。

1.2 土柱上力的平衡方程

设边坡表面方程为：z=s（x，y），s（x，y）≤h（x，y）。有：高度为h-s、截面积为d x d y的土柱上力的微分平衡方程：

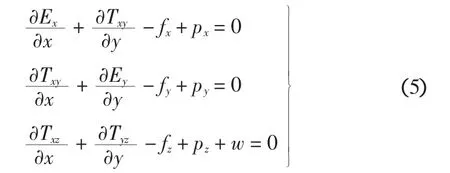
式中：Ex、Txy、Ey、Txz、Tyz分别为土柱间的柱间力，Ex=w是高度为h-s、截面积为单位面积的土体重力，px、py、pz分别为作用在边坡表面的x、y、z方向应力。

1.3 力矩平衡方程

在曲面 z=h（x，y）与边坡表面 z=s（x，y）围成的封闭区域Ω内，力矩平衡方程的一般组合形式为：

式中：A1、A2、A3为任意常数；xR、yR、zR为取矩点坐标。将式 （6） 改写为：

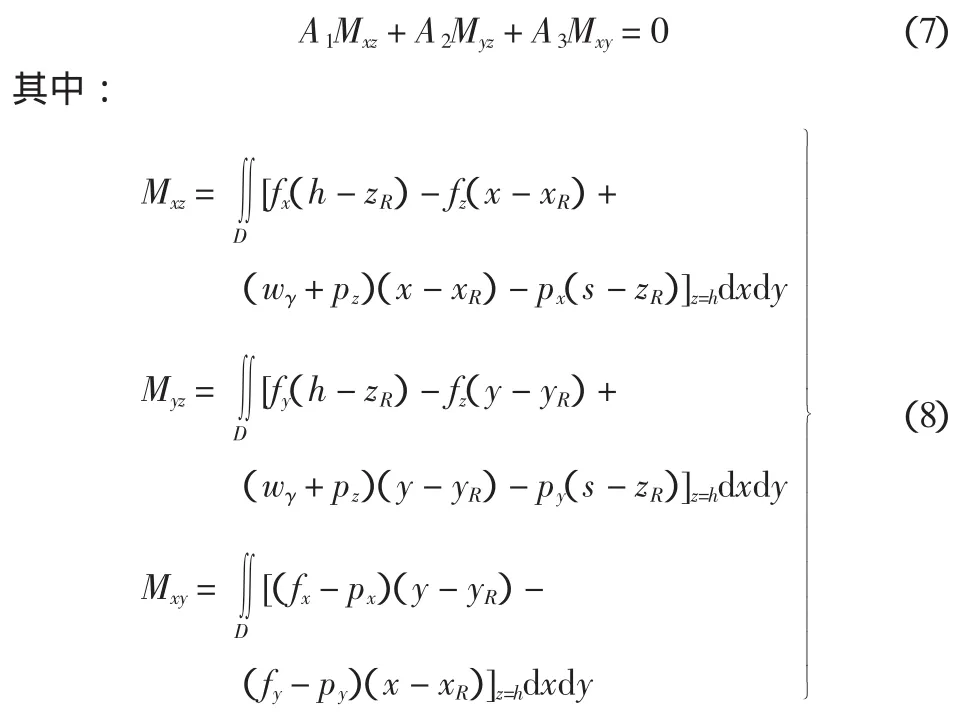
容易看出：Mxz是平行于oxz坐标面（y=0平面）的力产生的力矩之和；Myz是平行于oyz坐标面（x=0平面） 的力产生的力矩之和；Mxy是平行于oxy坐标面（z=0平面）的力产生的力矩之和；所以A1、A2、A3是平行于3个坐标面的力产生的力矩之和的组合系数，其意义是明确的。

2 分析方法的一般计算公式

由库仑屈服条件，式（2）可写为：

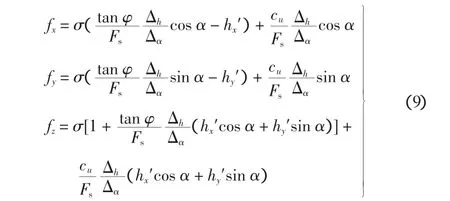
式中：cu=c-u tanφ

而由式（2）、式（5），有：

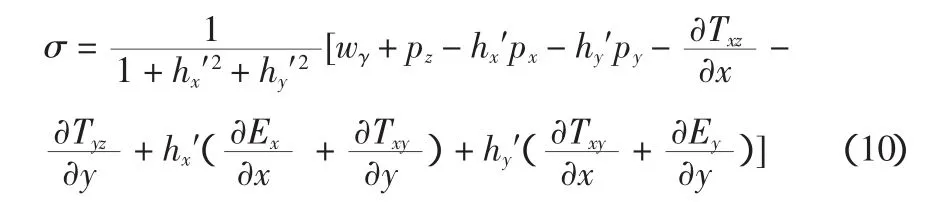
将式（9）、（10） 代入力矩平衡方程（6），整理得：

并略去δF（假定δF=0），就得出安全系数的一般计算公式：

式中：MR、M0分别为抗滑力矩、滑动力矩。

如果A1=A2=A3=1，则这一分析方法就是基于对空间一点（xR、yR、zR）力矩平衡方程的方法。

分析方法的假定条件只有一个：δF=0，这相当于假定：

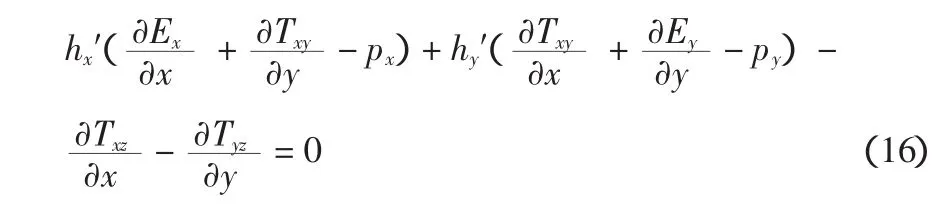
另外，在计算公式中，除含有可以适当选定的滑动面外，还有一个需要确定的α。对于滑动面上的任意一点，α可能都是不同的，或者说破坏方向可能是不同的；这是三维边坡稳定问题需要解决的一个问题。

下面，以常见的边坡形式为例，说明这一分析方法的应用。

3 坡顶局部区域作用荷载二维边坡

3.1 计算公式

二维边坡的坡顶局部区域作用荷载（图1），这是工程中常见的一种情况，应按三维问题计算。

如果坡顶局部作用荷载的区域和荷载、边坡（包括土层分布及相应的土性指标）、选取的滑动面均是关于y=0对称的，且取矩点的y坐标为yR=0。则这一问题是关于垂直平面y=0对称的。

在上述条件下，σ、cos α、hx′、h、（h-zR）、（x-xR）及 pz均是关于y的偶函数，而sinα、hy′、y均是关于y的奇函数 （py=0）。式 （14） 和式 （15） 可简化为：

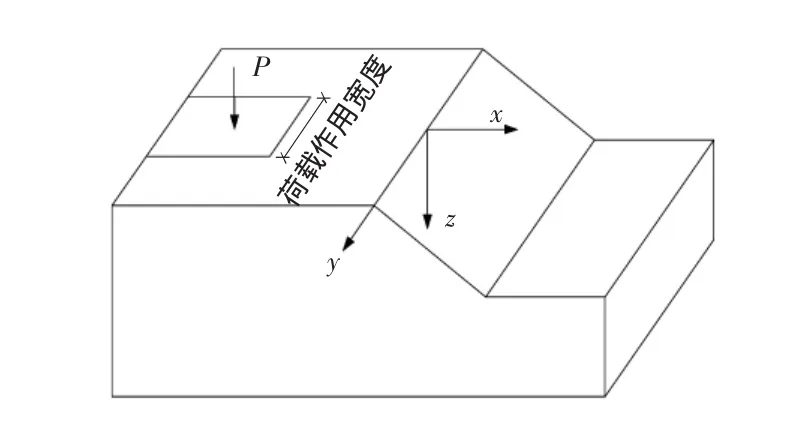
图1 局部作用荷载的边坡示意图

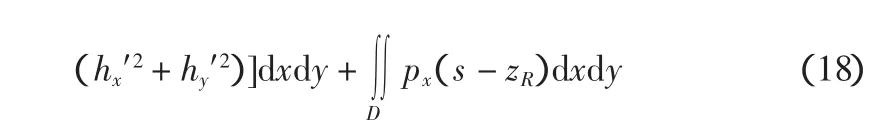
3.2 滑动面

目前，采用椭球面为滑动面较多[4，7]，如果滑动面采用椭球面：

式中：R、L为常数。式（17） 和式（18） 可简化为：

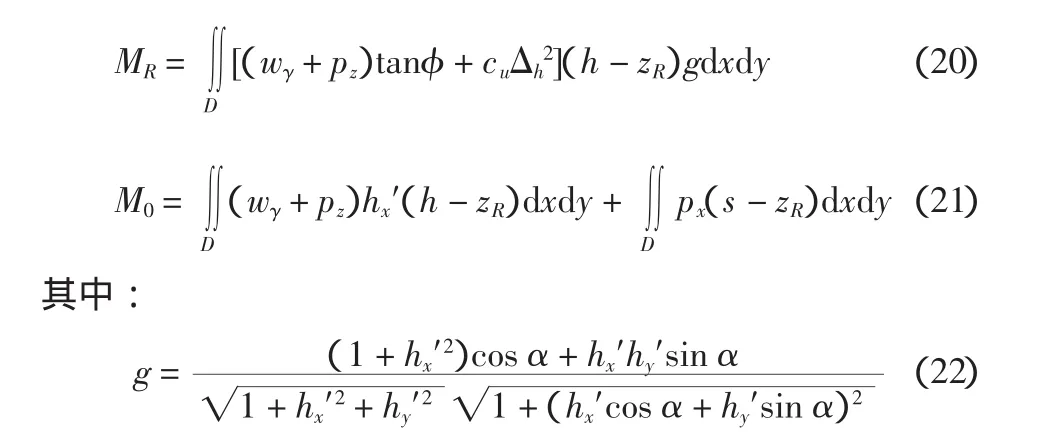
计算公式很简单，与二维边坡的简单条分法完全类似。

如果hy′=0、α=0，则g=1，公式在形式上就可以退化为二维边坡的简单条分法计算公式。

3.3 水平向破坏的方向角α

容易看出：这一公式相当于取：A1=1，A2=A3=0的情况。实际上，由力矩方程式（7） 可见，这是一种仅考虑水平破坏为x方向的确定方法；且因为边坡本身是二维的，所以水平破坏方向取为垂直于y=0平面的方向（平行于x方向），计算结果不会有太大的误差。也就是说，对这种边坡，可取α=0。

3.4 算例分析

设土质边坡对称于oxz平面（如图1所示），坡高20 m，坡顶、坡底水平，坡面与水平面夹角tanβ=0.5的坡度。坡顶局部区域作用荷载，且px=0。

计算中，采用滑动面为椭球面；并取α=0，不考虑孔隙水压力（u=0）。取不同的xR、zR、R、L，计算安全系数的最小值。对公式中的积分采用数值积分计算过程，这与通常的条柱法计算过程是相同的。

计算情况1：均质土边坡，c=18 kPa、φ=20°、25°，γ=17 kN/m3；坡顶上，在距坡肩2 m后的区域内，荷载作用宽度分别为15 m、30 m，作用pz=30 kPa、60 kPa均布荷载。计算结果如表1。

表1 坡顶局部作用荷载的二维边坡安全系数

计算情况2：两层土边坡，坡底面以上，c1=20 kPa，φ1=25°，γ1=17 kN/m3；坡底面以下，c2=10 kPa，γ2=17 kN/m3，取φ2=15°、20°；坡顶上，在距坡肩2 m后的区域内，荷载作用宽度分别为15 m、30 m，作用pz=30 kPa、60 kPa均布荷载。计算的安全系数见表2。

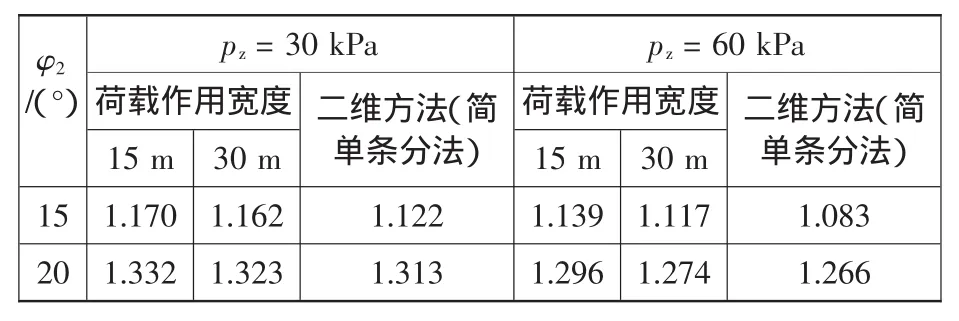
表2 坡顶局部作用荷载的二维边坡安全系数

首先注意，这种坡顶局部宽度内作用荷载的情况，安全系数不应小于按二维问题计算的结果，计算结果已经清楚地显示了这一点。

荷载作用宽度越小，安全系数越大，越与按二维问题计算结果接近。

无论是对均质土情况还是两层土边坡情况，荷载较大、作用宽度较小时，按三维计算与二维计算的安全系数相差已较明显，说明按二维计算的安全系数偏小了。但两者相差并不大，说明对这一方法计算中取α=0并未导致按三维计算的安全系数偏大过多；所以，取α=0可以满足工程计算所需的精度要求。

4 具有对称性的三维边坡问题

4.1 计算公式

实际问题中，存在大量对称的边坡问题，如海岸、河岸的护岸拐弯处，各种堤的堤头与拐弯处等（图2）。

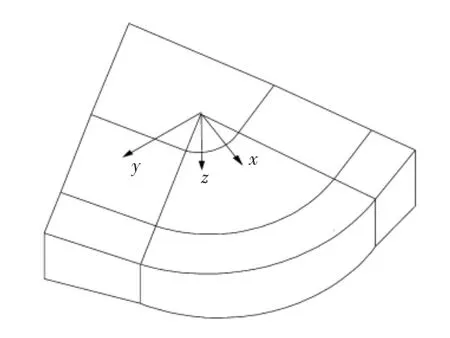
图2 三维边坡

适当的选取坐标系，均可归结为关于垂直平面y=0对称的边坡问题；即边坡表面作用荷载的区域和荷载关于y=0对称、边坡（包括土层分布及相应的土性指标）关于y=0对称、选取的滑动面也是关于y=0对称，则计算公式与式（17）、式（18） 是相同的。如果仍取滑动面为式（19） 的椭球面，计算仍为式 （20）、式 （21）。

例如，图3的三维边坡，其边坡表面为图4。

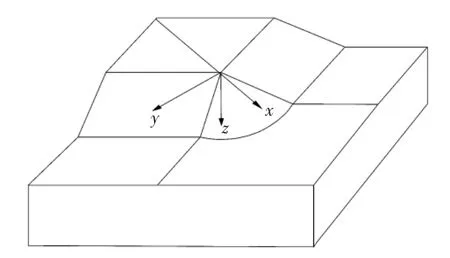
图3 三维边坡示意图

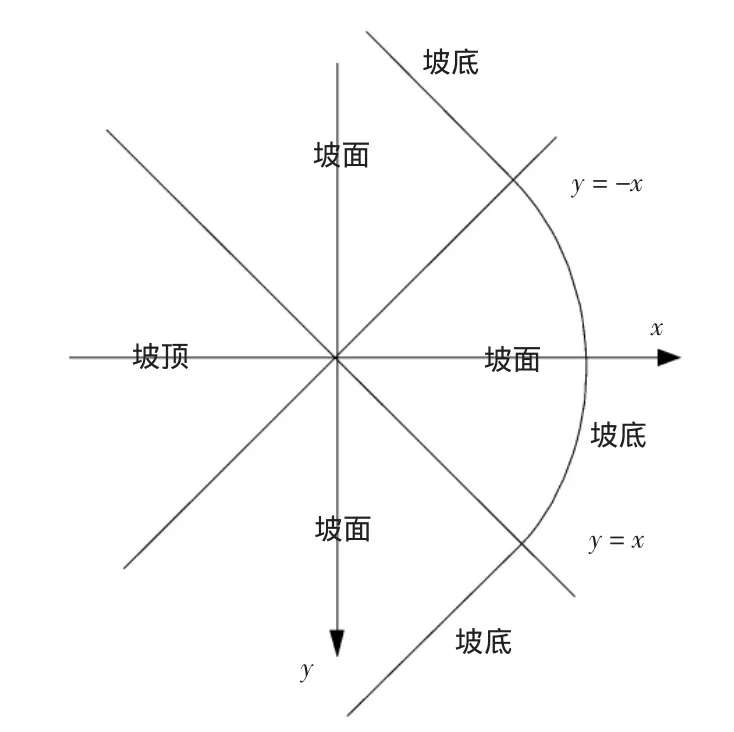
图4 三维边坡的水平面投影示意图

记：坡面与水平面夹角tanβ=B/H，B为坡面的水平宽度，H为坡高，则边坡表面为：

当：y-x≥0、且y+x≤0，为坡顶面：s=0.0；

当：y-x≤0、且 y+x≤0，为坡面：s= （x-y）tanβ/，其中，当（x-y）/≥B为坡底面s=H；

当：y-x≥0、且 y+x≥0，为坡面：s=（x+y）tanβ/，其中，当（x+y）/≥B为坡底面s=H；

4.2 水平向破坏的方向角α

对这种三维边坡，这里取以下两种确定方法进行试算，并通过计算结果分析其合理性。

1） α =0。

2）对滑动面上的任意一点，按距离坡脚线最近，且α为连续的原则选取：

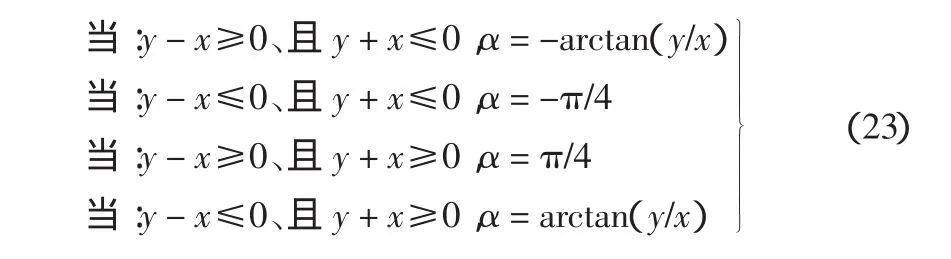
4.3 算例分析

设如图2所示的三维土质边坡，坡高20 m，坡顶、坡底水平，坡面与水平面夹角tanβ=0.5的坡度，坡顶无荷载。

坡底面以上，土性指标分别为c1=20 kPa、φ1=25°、γ1=17 kN/m3，和 c1=15 kPa、φ1=20°、γ1=17 kN/m3。坡底面以下，γ2=17 kN/m3，c2、φ2取不同值 （见表 3）。

表3 两层土三维土坡安全系数

同样，不考虑孔隙水压力（u=0）。并取不同的xR、zR、R、L，计算安全系数的最小值。由计算公式中的式（22） 及可以看出，不宜过小；所以限定≥0.25，且计算中剔除了使g＜0的滑动面。计算结果如表3.

当取α=0时，这显然是一种偏于不安全的确定方法，计算的安全系数显著偏大。说明对三维边坡，取α=0进行计算是不可行的。

对α选取方法2），这是一种根据边坡形状而确定的方法。当上层土强度指标大于下层土强度指标时，计算的安全系数较二维边坡的显著小，这是因为滑动面深度较大，滑动面通过下层土的面积较大。而当上层土强度指标显著小于下层土强度指标时，滑动面仅通过上层土，计算的安全系数较二维边坡小的不是很显著。一般的，计算的安全系数较二维边坡明显的小，说明计算的安全系数是合理的。所以，对这种三维边坡，按式（23）确定α进行计算是可行的。

5 一般的三维边坡问题

对一般的三维边坡，若不考虑边坡表面的水平力，取A1=A2=A3=1，滑动面为：

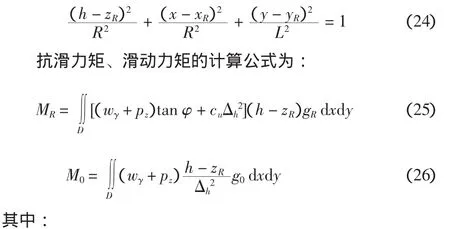
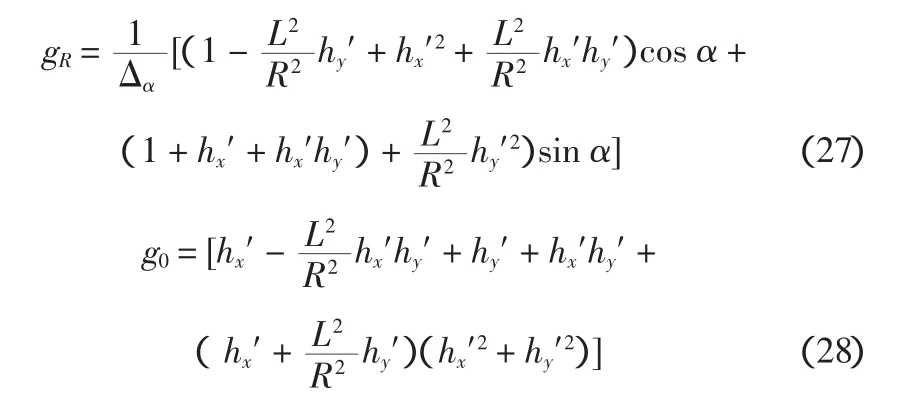
计算公式很简单，只要水平向破坏的方向角α确定了，即可计算出安全系数。但α如何确定？就需要进一步的研究。文献 [9]采用的α确定方法，即以式（27） 的gR取最小值来确定α不失为一种可供采用的方法。但这是一种偏于安全的方法，因为α作为剪应力方向余弦中的参数，已经体现在式（2） 中；而方法的计算公式是在式（2）的条件下得出的。

6 结语

1）只需要一个假定条件，获得了三维边坡稳定性分析的方法；且假定条件与二维问题简单条分法类似，计算公式简单，应用方便，具有广泛的应用意义。

2）具有对称性的三维边坡问题，如坡顶局部区域作用荷载二维边坡，海岸、河岸的护岸拐弯处，各种堤的堤头与拐弯处等，给出了水平向破坏的方向角α的选取方法。计算示例的计算结果表明，计算的安全系数合理。

最后说明，三维边坡稳定问题远较二维问题复杂；例如，对更一般的三维边坡，水平向破坏的方向角α如何确定？尚需进一步研究。

[1] Duncna JM.Staye of the Art：Limit Equilibrium and Finine-element Analysis of Slopes[J].Journal Geotechnical Engineering，ASCE，1996，122（7）：577-596.

[2]Huang CC，Tsai CC.New Method for 3Dand Asymmetrical Slope Stability Analysis[J].Journal of Geotechnical and Geoenvironmental Engineering，2000，126（10）：917-927.

[3] 冯树仁，丰定祥，葛修润，等.边坡稳定性的三维极限平衡分析方法及应用[J].岩土工程学报，1999，21（6）：657-661.

[4] 陈祖煜，弥宏亮，汪小刚.边坡稳定三维分析的极限平衡法[J].岩土工程学报，2001，23（5）：525-529.

[5] 李亮，迟世春，郑榕明.基于椭球滑动体假定和三维简化JANBU 法的边坡稳定分析[J].岩土力学，2008，29（9）：2 439-2 445.

[6]Zhu DY，Lee CF，Jiang H D.Generalised Framework of Limit E-quilibrium Methods and Numerical Procedure for Slope Stability[J].Geotechnique，2003，53（4）：377-395.

[7] 陈祖煜.土质边坡稳定分析～原理·方法·程序[M].北京：中国水利水电出版社，2003.

[8] 朱大勇，丁秀丽，邓建辉.基于力平衡的三维边坡安全系数显式解及工程应用[J].岩土力学，2008，29（8）：2 011-2 015.

[9] 李树奇，黄传志，曹永华，刘爱民.三维边坡稳定问题的基本方程与分析方法[J].岩土工程学报，2010，32（12）：1 892-1 897.