综合孔径辐射计反演成像算法研究

晁 坤 陈后财 赵振维 吴振森

（1.西安电子科技大学，陕西 西安 710071；2.中国电波传播研究所，山东 青岛 266107）

1.引 言

从上世纪50年代开始，射电天文学中的综合孔径技术被引入到辐射计的研究当中，极大地推动了被动遥感技术的发展。它的基本思想是采用空间频率域的测量代替传统辐射计对空间域的直接测量，具有高分辨率等优点［1］。综合孔径辐射计的基本构成单元是二元干涉仪，通过不同长度基线的干涉测量结果进行处理从而反演被观测区域的亮度温度分布［2－3］。由于多天线单元的孔径综合作用，可提高天线阵的空间分辨能力。目前用于遥感等的综合孔径辐射计为了能够获得高空间分辨率通常可采用无冗余设计。无冗余天线阵列使U－V频率覆盖点（空间频率采样点）尽量多，从而提高反演效果。当天线阵列的分布确定后，采用合适的反演成像算法反演被测物的亮度温度分布是综合孔径辐射计被动探测系统的关键问题之一。

何云涛等学者根据可视度函数（Visibility Function，VF）与目标亮度温度之间为傅里叶变换的关系，提出了各种基于傅里叶变换的反演算法并已成功地用于“U，T，十”形天线阵结构的成像系统中［4］；1978年 Stogryn把 Backus－Gilbert理论应用于星载机械扫描成像系统的反演问题上（BG算法），取得了较为理想的反演数据。但这两种算法都有一定的缺陷，前者对硬件系统要求很高且成像误差大；后者G矩阵的测量要求比较严格，且运算量大，速度慢，实现时灵活性不够。总结前人算法，提出了一种基于视场细分的综合孔径辐射计反演成像算法，较好地克服了以上两种方法的不足，具有广泛的应用价值。

2.综合孔径辐射被动成像的傅里叶变换法

目标亮度温度与可视度函数之间的傅里叶变换关系适用于任何综合孔径辐射计。为方便论述，以二维圆周综合孔径辐射计为研究对象，基本构成单元是二元干涉仪，即天线阵中任意两天线形成的子阵列，如图1所示。

图1 二元干涉仪示意图

在理想信道的情况下，n元阵列的可视度函数及反演亮温存在如下关系

式中：（u，v）是第i，j个天线对应的可视度函数，其对应的归一化采样点坐标为 （uij，vij），uij＝ （xixj）／λ，vij＝ （yi－yj）／λ；（xi，yi）、（xj，yj）分别为天线单元i，j的坐标；T（ξ，η）为视场中 （ξ，η）点处的亮温。

可得目标反演亮温为

在实际测量中，得到的Vij（u，v）是从n个天线单元上接收到信号做的复相关函数。由于空间频率采样点（下文简称为采样点）数不可能无限多，只能得到离散的采样点上的可视度函数值，即有

式（3）中包含n2－n＋1个离散采样点。这是综合孔径辐射计傅里叶反演算法的基本原理［5］。这种方法得到的亮温反演结果显然和实际亮温值有较大差异，只有增加采样点数才能提高反演效果。为了弥补此种方法的采样点不足，现在使用较多的方法是采用插值技术将采样数据插值到规则网格点上，然后再利用傅里叶变换来进行快速成像。

假设将原来的n2－n＋1个采样点插值成（2P＋1）（2Q＋1）个，则式（2）可转化为

式中：Vpq（up，vq）为插值后的第 （p，q）个可视度函数；（up，vq）为第 （p，q）条基线在X轴和Y轴上的投影；T（p，q）为插值后对应第 （p，q）采样点处的反演亮温。

此方法具有运算速度快的优点，但可视度函数的插值存在很大的误差，且不同的阵列排列需要根据采样点的分布特征采用不同的插值方法。如“Y”形阵可采用六边形网格插值算法，圆形阵采用伪极网格插值算法，相当繁琐且会造成反演图像的失真。在实际探测时，由于天线及接收机的误差会导致可视度函数的测量过程中出现各种偏差，不能直接利用测得的可视度函数值通过傅里叶变换求得亮温分布，必须经过严格的校正。

3.基于Backus－Gilbert理论的反演算法（BG算法）

BG算法的核心思想是通过测量各个基线的点源响应，也称为基函数来反演亮温［6－7］。将式（1）离散化后写成矩阵相乘的形式，得

式中：V是含各采样点（ij序列）的可视度函数值形成的一维数组，共n2－n＋1个；T为P×Q的二维矩阵，T（l，m）反映的是探测区域中 （l，m）点处的真实亮温；令N＝n2－n＋2，则G为N×P×Q的三维矩阵，也称为调制矩阵。显然，G矩阵的各元素由各基线的基函数确定，可以通过测量各基线的点源冲击响应求得。其中P，Q取值越大，反演图像越平滑。在V，G确定的情况下，由式（2）根据Backus－Gilbert理论，即可得反演亮温为

式中：GH为G的共轭转置矩阵。

只要测出系统矩阵C并固化，再测出各采样点对应的可视度函数V，就能反演出亮温.此算法可在保证综合天线方向图归一化的前提下得到很好的反演成像。但是，存在的突出问题是G矩阵测量困难，求C矩阵时计算量过大，不利于实时成像。一旦C矩阵为病态矩阵，很小的可视度函数误差便可能带来很大的反演成像误差。

4.基于视场细分的改进反演算法

提出一种基于视场细分的反演成像算法，并考虑了实际系统的误差。

由前述可知，矩阵形式的理想模型为

实际模型，对可视度函数引入一个不可消除的误差分量所组成的矩阵E，定义如下

则，有误差时的V矩阵为＝E·V

假设存在一P×Q×N阶的三维矩阵K，使得真实的反演亮温为：

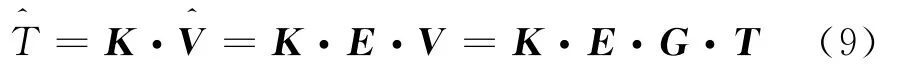
引入亮温误差矩阵△T：

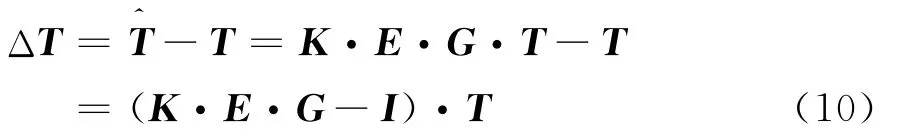
采用亮温误差矩阵中所有元素的均方差来衡量误差对成像影响的大小

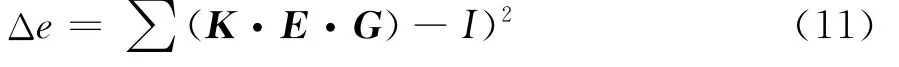
为方便计算，将G矩阵变换成N×P·Q的二维矩阵，将K矩阵变换成P·Q×N的二维矩阵，则可得Δe最小时的K的最小二乘解为

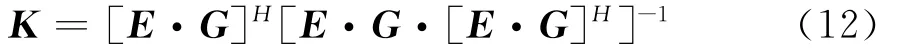
此时K是BG算法中包含误差的系统调制矩阵C。

在不考虑误差的情况下，

即为采用BG算法时理想情况下的系统调制矩阵，如式（6）所示。

改进的反演成像算法只计算主对角上的误差，即不考虑各亮温之间的相互“干扰”，则每个细分后的子视场的误差为

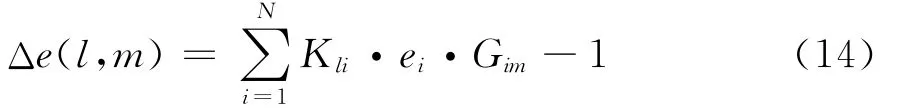
若各误差的符号相同，则Δe（l，m）达到最大值，即每个子视场的自身误差占主导地位，反演成像效果最好。所以采用此算法不需要严格的校准可适度函数，而只要将各可视度函数校成在同方向变化（都偏大或都偏小）即可。通过仿真分析可知这种方法是可行的，它可以使系统中不可消除的误差分量对反演成像的影响最小化。需要注意的是此反演模型只考虑了主对角上的元素，并未考虑各反演亮温之间的影响，所以用于点源或亮温分布均匀的面源效果较好，对于视场亮温分布比较复杂时的反演效果还有待研究。

因此，若有

由式（9）、（16）得实际反演亮温的表达式为

式（17）与式（2）给出的亮温反演表达式的离散情况是一致的，说明能很好地反演出亮温，且对误差有很好的抑制作用。式（17）的物理意义为：某点的反演亮温实际上是将每个采样点得到的此点亮温的累加，因此，第（l，m）个矩形区域的反演亮温T（l，m）为采样点从k＝1到k＝N所得亮温的和。令

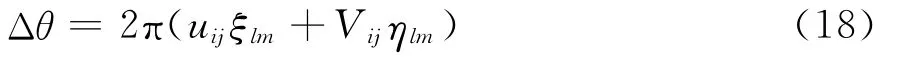
由于采样点总是关于原点对称分布，且原点为自相关对应的采样点，所以可将可视度函数写成复数形式

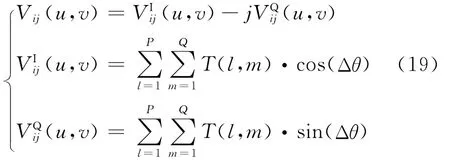
和为正交的两路采样信号，故式（17）可化为

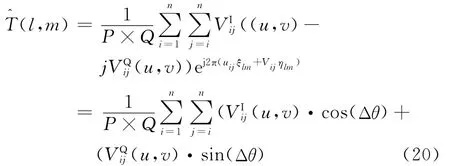
因此，只要通过各天线单元接收到的信号求出可视度函数Vij（u，v）并进行简单地校正，便能按P×Q按个像素很好地反演出视场中对应像素的亮温。算法的实质是通过对视场的细分来提高了采样率并可使误差对成像质量的影响最小化。此方法简单实用，不需严格的校准可视度函数的测量误差，既弥补了傅里叶变换算法及BG算法的一些缺点、准确、快速。

5.仿真分析

通过仿真分析，着重比较BG算法和视场细分改进算法。假设目标为正方形形状，接收到的等效亮温为250K，背景亮温为0K。

阵列为16单元圆周阵，阵列排布方法见参考文献［8］［9］。图2给出了仿真的原始图像。两种算法在不同测量误差情况下的成像结果如图3所示，图像分辨率均为100×100像素。此处引入均方误差来判断不同方法成像的质量。成像结果与原始图像的均方误差按如下公式计算：

图2 仿真分析原始图像

式中：ti为第i个像素的反演亮温；Bi是其对应的目标真实亮温；N为成像像素总数。表1列出两种算法成像耗时及与原始图像均方差的对比结果。

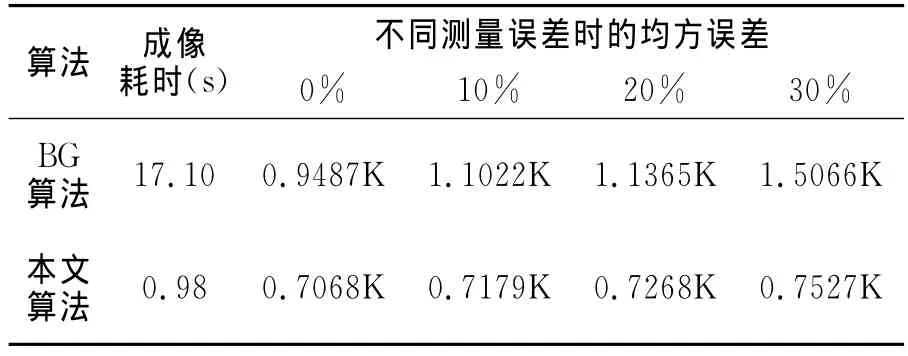
表1 两种算法成像耗时及均方误差对比

综上所述，传统傅里叶反演变换成像算法若使用简单的插值方法成像效果是比较差的，且对硬件设备的要求很高，所以使用傅里叶反演变换成像算法用于实际的系统会使成像存在很多不可消除的误差，影响了成像的质量。傅里叶反演变换成像算法的优点是它的成像速度快。

BG算法的成像效果要明显好于傅里叶反演变换成像算法，成像清晰。此算法可在保证综合天线方向图归一化的前提下得到很好的反演成像，但是存在的突出问题是G矩阵测量难，求其逆矩阵C矩阵时计算量过大，不利于实时成像。且C矩阵为病态矩阵，所以很小的可视度函数测量误差便可能带来巨大的反演成像误差。

相比而言，在系统具有不可消除的误差分量时，视场细分反演成像算法的成像效果相对BG算法有进一步提高，成像清晰。其突出的优点是在成像清晰的前提下，运算耗时非常小。它弥补了以上两种算法的缺点，可以很好地用于实际的实时成像系统中，而且因为计算每个细分后视场的亮温是相互独立的，故可采用高性能计算机进行多线程并行运算。本文采用该算法成像仿真所耗时间是在MATLAB下使用单线程处理的，如采用n线程并行计算，则实际运算速度会快n倍。

6.结 论

反演成像算法设计是综合孔径辐射计的关键技术之一。本文提出了基于视场细分的新反演成像算法。该方法将视场细分成等大小的矩形子视场，然后分别对各子视场反演成像，仿真分析表明该算法成像效果好，运算速度块，证明了此算法的正确性和有效性，对综合孔径辐射计实际应用系统的反演成像算法设计具有重要的参考价值。

［1］吴 季，刘 浩，阎敬业，等.干涉式被动微波成像技术 ［J］.遥感技术与应用，2009，24（1）：1－12.

WU Ji，LIU Hao，YAN Jingye，et al.Interferometric imaging technology for passive microwave radiometry［J］.Remote Sensing Technology and Application，2009，24（1）：1－12.（in Chinese）

［2］胡岸勇，苗俊刚，薛 永，等.BHU－2D干涉综合孔径微波辐射计反演算法研究 ［J］.微波学报，2009，25（2）：87－91.

HU Anyong，MIAO Jungang，XUE Yong，et al.Reverse algorithm of BHU－2Dinterferometric synthetic aperture radiometer ［J］.Journal of Microwaves，2009，25（2）：87－91.（in Chinese）

［3］郎 锐，郭华民，赵振维.综合孔径微波辐射计天线与信道模型仿真 ［J］.电波科学学报，2007，22（5）：794－798.

LANG Rui，GUO Huamin，ZHAO Zhenwei.Simulation of antennas and channels model for synthetic aperture radiometer［J］.Chinese Journal of Radio Science，2007，22（5）：794－798.（in Chinese）

［4］何云涛，江月松，陈海亭.二维圆周综合孔径阵列优化及其毫米波成像特性研究 ［J］.遥感学报，2007，11（1）：33－38.

HE Yuntao，JIANG Yuesong，CHEN Haiting.Studies of optimization and imaging properties of two－dimensional circle array for mm－wave synthetic aperture system［J］.Journal of Remote Sensing，2007，11（1）：33－38.（in Chinese）

［5］CORBELLA I，TORRES F，CAMPS A，et al.Brightness－temperature retrieval methods in synthetic aperture radiometers［J］.IEEE Transactions on Geoscience and Remote Sensing，2009，47（1）：285－294.

［6］TANNER A B，SWIFT C T.Calibration of a synthetic aperture radiometer［J］.IEEE Transactions on Geoscience and Remote Sensing，1993，31（1）：257－267.

［7］WU Ji，HUANG Yonghui，DONG Xiaolong.Image retrieval algorithm of two－dimensional synthetic aperture radiometer［C］／／International Geoscience and Remote Sensing Symposium（C）.2001.

［8］胡岸勇，苗俊刚.二维综合孔径辐射计中的稀疏天线布局 ［J］.遥感技术与应用，2007，22（2）：158－161.

HU Anyong，MIAO Jungang.Thinned array on 2D synthetic aperture radiometer ［J］.Remote Sensing Technology and Application，2007，22（2）：158－161.（in Chinese）

［9］晁 坤，赵振维，吴振森，等.基于微分进化算法的综合孔径辐射计圆阵优化 ［J］.电波科学学报，2009，24（6）：997－1001.

CHAO Kun，ZHAO Zhenwei，WU Zhensen，et al.Optimization of synthetic aperture radiometer circle array based on differential evolution algorithm ［J］.Chinese Journal of Radio Science，2009，24（6）：997－1001.（in Chinese）