一种基于梯度Hough变换的同心圆检测新方法

陈 星（厦门大学自动化系，福建 厦门 361005）

一些常见的平面规则图形，如直线、圆形、椭圆形、三角形、正方形等在工业产品检测、生物信息提取、集成电路板在线质量检测、交通标志识别等领域等有着广泛的应用[1]。对于直线、圆形等检测问题，已经提出了大量实用的检测方法，但对于同心圆检测问题，目前没有专门的检测算法，部分学者在这一方面做了一定的研究，如文献[2]提出的基于弦中点Hough变换的同心圆检测方法，这种方法虽然能比较好地检测出同心圆，但每次都要重复遍历边缘特征点找到弦中点，当图中同心圆每增加一个，算法复杂度会剧烈增大，这样就不利于对存在很多同心圆的图像进行检测。文献[3]给出了一种同心圆检测中的区域划分算法，在圆心已知情况下用最小二乘法拟合圆，但没有给出具体的圆心计算方法，且仅适合于固定区域划分层次。

目前，有许多检测圆的算法，Hough变换是检测圆的一种常用方法，由Paul Hough在1962年提出[4]，它的突出优点是可以将图像中较为困难的全局检测问题转换为参数空间中相对容易解决的局部峰值检测问题[5]。本文将提出一种基于改进的Hough变换的二次检测同心圆的算法，先用一种改进的Hough变换算法检测圆，再将检测到的圆进行破坏后，进行第二次圆检测，最后判断前后检测到的圆的圆心和半径的关系来判断其是否为同心圆。这种算法克服了以前同心圆检测算法缺点，一方面缩小了检测同心圆的局限性，另一方面提高了检测效率，并用仿真和应用实例证明了算法的高效和准确性。

1 改进的梯度Hough变换检测圆(IGHT)

圆的一般方程为：

在对圆进行检测的时候，往往只需要得到该圆的边界信息，这就要用到边缘检测，一阶导数可以用于检测图像中的一个点是否是边缘点。

图像f（x，y）在（x，y）的梯度定为如下方向：

梯度向量指向在坐标（x，y）的f的最大变化率方向。由向量分析得：

其中 表示向量 在（x，y）处的方向角，角度以x轴为基准度量，边缘在（x，y）处的方向与此点的梯度向量的方向垂直[6]。文献[7]提出了一种梯度Hough变换来检测圆方法，用极坐标方程表示圆：

在事先知道半径情况下，用求圆边缘上每一点的梯度方向角和根据边缘点的坐标（x，y）来求圆心坐标（a，b），这样必须预先知道所求圆的半径范围，有较大局限性，所以在此基础上对GHT方法进行改进。

如图1所示，圆上所有点的梯度方向都是指向圆心的，圆边缘上所有的法线必相交于圆心。

传统的Hough变换用三维累加器A（a，b，r）累加来求得圆心和半径[8]，图像平面的方程转化为参数平面上的示意图如图2所示，这样每次检测圆都要遍历整个三维参数空间，耗费大量内存，计算量巨大。为了降低HT方法累加器维数，累加过程分两个阶段进行：第一阶段，遍历图像，求边缘梯度，通过Hough变换在参数空间的二维累加器A累加，通过累加的局部峰值确定圆心；第二阶段，再遍历图像边缘点，用一个一维累加器B累加半径，出现频率最高的半径作为此圆心对应半径。

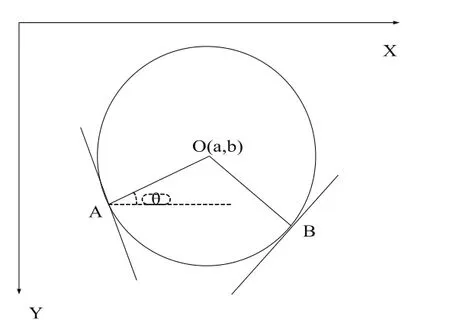
图1 圆心位于圆边缘点法线交点

图2 圆的Hough参数空间

2 基于IGHT的二次检测的同心圆检测算法

改进的梯度Hough(IGHT)变换方法的优点是图像中存在圆交叉、圆互相包含等情况时，仍能检测出圆，但是当有同心圆时，只能检测出同心圆中最小的一个。如图3所示。

图3 IGHT检测到的同心圆中的小圆

基于此，本文提出先用IGHT方法进行第一次圆检测检测到小圆，记录圆心（x1，y1），和半径r1。对此圆进行破坏，分割出外圆，再使用IGHT进行第二次Hough圆检测，再次记录圆心（x2，y2）和半径r2。定义距离：

具体算法步骤如下：

步骤1 原图像预处理（图像灰度化，高斯平滑滤波）；

步骤2 对图像进行CANNY边缘检测，并二值化保存为EDGE图像；

步骤3 预处理后的原图进行第一次IGHT圆检测；

步骤4 破坏第一次检测到的圆，即将EDGE图像中检测到的圆的 的圆环内的像素值全部设为0，将这些圆去除，得到图像DST；

步骤5 对DST图像预处理，先灰度化，再高斯平滑滤波；

步骤6 第二次IGHT圆检测；

步骤7 两次检测到的圆比较，判断是否为同心圆，并在原图中画出同心圆位置。

设预处理后的圆的边缘有N个边缘点，IGHT方法对圆心需要进行（梯度方向直线）2维投票的次数是N。

设图像上边缘特征点坐标为 ，与圆心的距离记为d（p（j），（a，b）），

通过和函数S进行半径累积：

其中N为圆边缘特征点个数。则Smax累积半径rk为关于（a，b）存在圆的半径，故对半径进行1维投票的次数同样为N。则每次用IGHT方法检测圆的复杂度为：

每次用赋值法去掉小圆的复杂度为：

假设图像有k个同心圆，则整个算法复杂度为：

而文献[2]提出的算法复杂度为

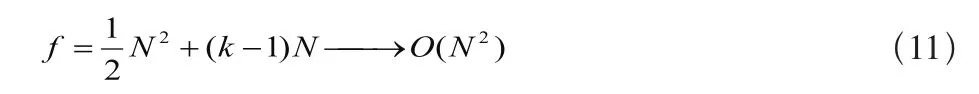
说明本文算法执行效率更高。

3 实验仿真

仿真实验在2.6GHz PC机上应用VS 2008 软件开发平台完成，编程语言为C++，并采用OpenCV-2.1库进行图像相关处理，下面分别对468×473的三幅图片先进行CANNY边缘检测再进行同心圆检测。图5为成功检测两个不完整的圆的同心圆的图片，图6为存在干扰曲线仍成功检测到同心圆的图像，图7为成功检测到3个同心圆的图像，其中圆心的位置都有标注。对于有多个同心圆的情况此算法仍然适用。通过仿真结果和数据，可以看到此算法准确度高，计算速度快，而且有较好地抗干扰性。

图5 含两个半圆同心圆的检测结果

图6 含干扰的同心圆检测

图7 含3个同心圆的检测结果

图5 ~图7的算法处理时间如表1所示。

表1 本文样本图同心圆检测的算法处理时间（处理时间为10次运算的平均值）

4 应用实例

基于此算法的实用性，将此算法成功应用于茶杯茶壶识别实例中（茶具中不添加其它圆形干扰物体），通过基于IGHT同心圆检测方法检测出有同心圆处的位置的为茶壶，是圆而非同心圆的位置为茶杯，并成功标记茶杯和茶壶位置和个数。

从茶具正上方拍摄一幅图片，图片分辨率为320 240。如图8，(a)为基于VS 2008 软件开发平台和OpenCV库的茶杯茶壶识别软件用户界面，(b)，(c)，(d)，(e)，(f)为算法过程图以及识别结果图。第一次检测到的圆A，B，C，D圆心分别为(144,130)，(244,116)，(32,168)，(204,44)，半径分别为42，34，26，31。第二次检测到的圆E圆心为（144,136），半径为60。这里定义 为0.15，根据公式(5)说明圆A与圆E为同心圆，同心圆所在位置为茶壶，圆B，C，D为茶杯所在位置，时间为69.34ms。

5 结语

日常生活包含同心圆的物体大量存在，如果能方便检测出同心圆，那么将容易检测出包含同心圆的物体，因此研究同心圆检测算法在实际应用中有着十分重要的意义。本文结合IGHT检测圆的方法和二次检测法，高效并准确地检测出图像中的同心圆，并将此算法成功应用到茶杯茶壶识别中去，证明了此算法的实用性。通过仿真可以看出此算法对半圆弧仍然能准确检测，抗干扰性较强，而且检测速度较快，不需要事先确定圆心，半径，在检测圆的局限性上有所改善，说明了此算法的优越性。

图8 本文算法处理过程图以及识别结果

[1] 秦开怀, 王海颖, 郑辑涛. 一种基于Hough变换的圆和矩形的快速检测方法[J]. 中国图象图形图像学报, 2010, 15(1).

[2] 王磊，陈临强. 基于弦中点Hough变换的同心圆检测方法[J]. 计算机应用, 2009, 24(7).

[3] 牛建军, 刘上乾, 韩宝君, 任宝文. 同心圆检测中的区域划分算法[J]. 光子学报, 2006, 35(12).

[4] P.V.C.Hough. Method and means for recognizing complex patterns[P].U.S.Pattern, 3069654, 1962, 12: 18.

[5] 夏磊, 蔡超, 周成平, 丁明跃. 一种用Hough变换检测圆的快速算法[J]. 计算机应用与研究, 2007, 24(10).

[6] RAFAEL C.GONZALEZ，RICHARD E.WOODS. 数字图像处理（第二版）. 电子工业出版社, 2007. 8. 467-474.

[7] 瞿钧, 甘岚. 梯度Hough变换在圆检测中的应用[J]. 华东交通大学学报,2007, 24(1).

[8] C.KIMME, D.H.BALLARD, J.SKLANSKY, “Finding circles by an array of accumulators”, Communications of the Association for Computing Machinery 18(1975):120-122.