弹体高速入水特性实验研究＊

张 伟，郭子涛，肖新科，王 聪

（哈尔滨工业大学超高速撞击研究中心，黑龙江 哈尔滨150001）

对入水问题的初期研究始于20世纪20～30年代，二次大战促使对入水问题的研究拓展到入水过程中的空泡现象和水下弹道等各个方面。早期开展的水弹道研究，是从鱼雷弹道开始的［1－2］，J.G.Waugh［1］、A.May［3］对弹体入水特点和实验结果进行了总结。早期也进行了一些关于高速弹体入水的初步实验，但研究工作相对较少。矶部孝［4］研究了常规兵器水下弹道的运动规律并开展了大量的实验，对弹丸入水跳弹的现象作了深入的分析并对弹丸的稳定机理作了简要分析，但未考虑空化及空泡的影响。近来，随着超空化减阻特性的发现，以及以俄罗斯“暴风雪”超空泡鱼雷为代表的水下高速超空泡武器的成功研制，弹体的高速入水特性以及水中弹道规律更是受到世界各国的广泛关注并纷纷开始超空泡武器的研制工作。超空泡鱼雷行进时要藏身于弹体头部产生的空泡，而这种空泡的产生和形状、尺寸均与弹体头部的形状有密切关系，同时，弹体头部形状和弹体速度直接影响着弹体对水下防护壳的侵彻能力。本文中，对平头、卵形和截卵形弹体入水进行实验研究，利用高速摄像机记录不同头型弹体水平高速入水的过程及弹道轨迹，并对弹体头部形状、水下空泡特性、弹体速度和侵彻深度等关系进行探讨。

1 实验装置

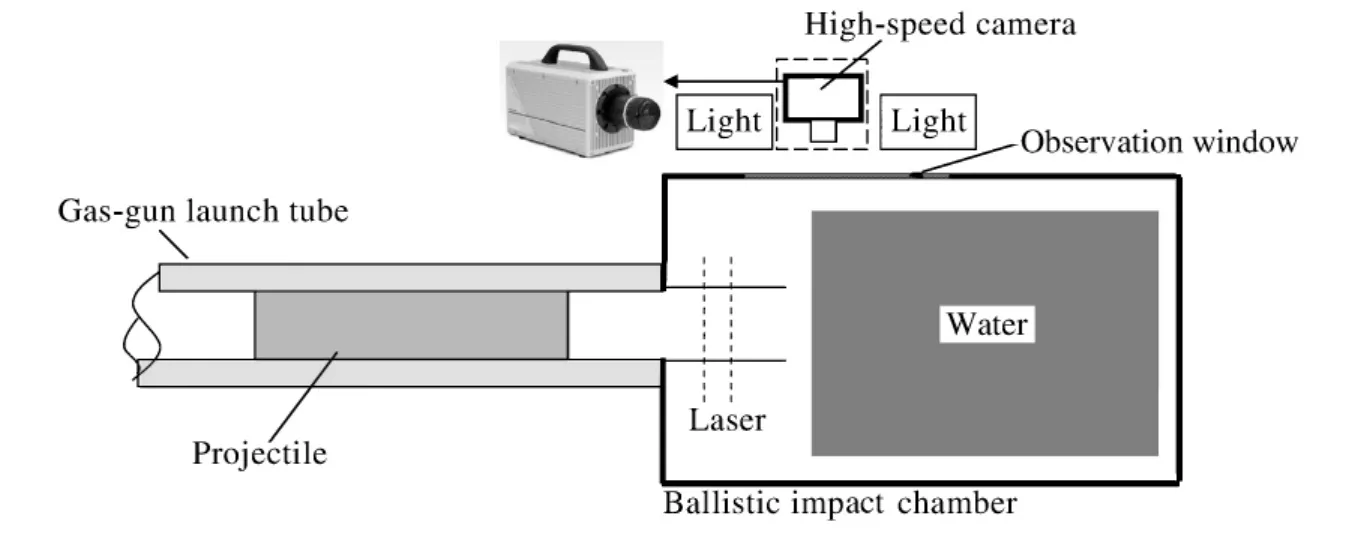
图1 撞击实验设置示意图Fig.1 Sketches of impact experimental set－up

实验装置包括一级气体炮发射设备、激光测速装置、水容器以及光学相机等几个部分，如图1所示。水容器尺寸为360 mm×360 mm×600 mm，一侧为透明聚碳酸酯板窗口，相机可通过它观察弹体在水中飞行的弹道轨迹，水容器的弹体入射口端用圆形塑料薄膜密封。采用Photron Ultima APX－RS型高速相机，帧率为36 000 s－1，光照系统采用2个1.2 k W的照明灯。实验弹体分为平头、截卵形及卵形3种，材料为38CrSi钢，弹径均为12.65 mm，图2为弹体尺寸示意图。平头弹长度25.4 mm。卵形弹分为：（1）头部圆周曲率φ＝1，长43.6 mm；（2）φ＝1，长30.6 mm；（3）φ＝3，长36.0 mm。截卵形弹体分为：（1）φ＝1，长27.3 mm；（2）φ＝3，长28.4 mm。D1都为8.41 mmm。

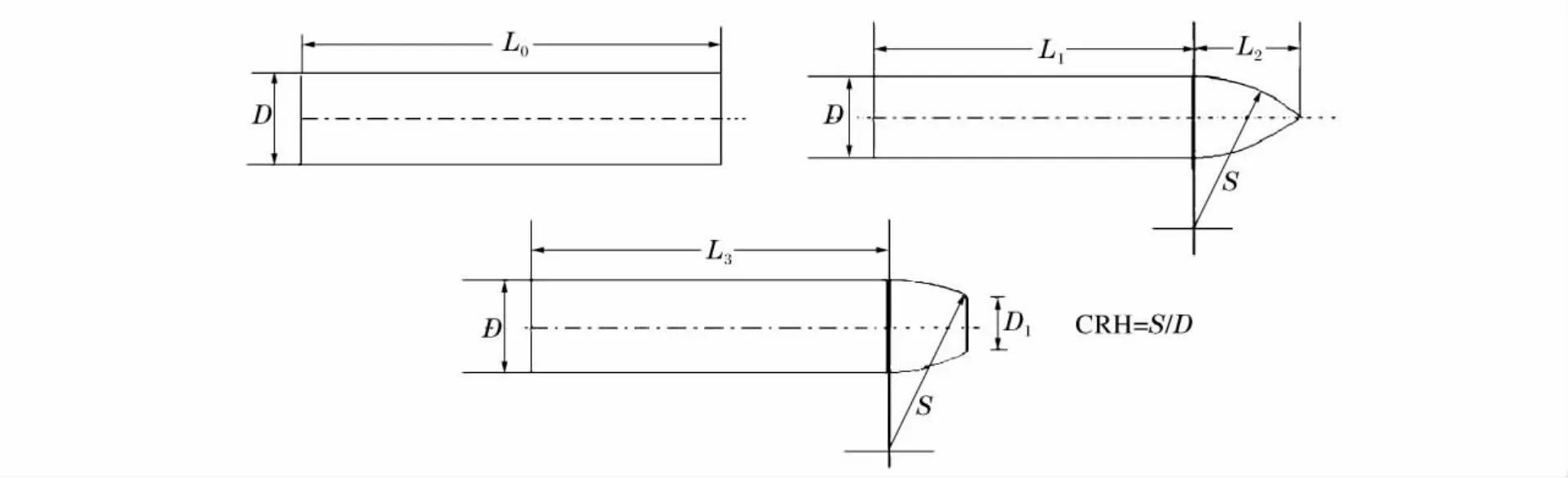
图2 弹体尺寸示意图Fig.2 Sketches of projectile dimensions

2 实验结果及分析

2.1 弹道稳定性分析

当弹体在水中超过一定速度时，空泡在弹体周围形成并把弹体包裹起来，直至形成超空泡，此时整个弹体将只有弹体头部与水接触，因此弹体的头部形状将影响着水中弹体的运动姿态、速度以及空泡的形状。以下将分别讨论3类弹体入水的弹道稳定性。

2.1.1 平头弹入水弹道轨迹

平头弹体入水速度范围在35～142.7 m/s之间，图3为平头弹体在初速度为95.4 m/s时的入水空泡扩展过程。平头弹体在入水过程中表现出良好的稳定性，没有发生偏转且入水空泡扩展过程都经历了开空泡、空泡颈缩、空泡闭合及空泡溃散4个过程。

图3 平头弹体在初速度为95.4 m/s时的入水过程Fig.3 Water entry process of flat－nosed projectile at the velocity of 95.4 m/s

2.1.2 截卵形弹入水弹道轨迹

实验发现截卵形弹体一般都是在入水前期基本稳定，后期则由于弹体头部受力不均衡而发生偏转。两种截卵形弹体入水前期形成的空泡形态基本相似。图4为φ＝3的截卵形弹体在初速度为113.6 m/s时的入水过程。

2.1.3 卵形弹入水弹道轨迹

共进行3种卵形弹体的入水实验，图5（a）为长30.6 mm的卵形弹（φ＝1）的入水过程，与图5（a）中弹体质量相同但φ＝3的卵形弹体的入水过程如图5（b）所示。相对其他两种头型弹体，卵形弹体在水中飞行时最容易发生偏转，稳定性与弹体的总长度和弹体头部圆周曲率有关，长度的增加会加大弹体在水中偏转的时间，同时，卵形体头部φ越大即越锐利，弹体越容易发生偏转。

图4 φ＝3的截卵形弹在初速度为113.6 m/s时的入水过程Fig.4 Water entry process of truncated－ogival projectile（φ＝3）at the velocity of 113.6 m/s

图5 卵形弹的入水过程Fig.5 Water entry processes of ogival projectiles

2.2 柱形入水弹体速度衰减规律

由于平头弹体在水中运行最稳定，因此本文中只讨论柱形弹体在水中的衰减规律。根据实验中拍摄的照片时间间隔以及弹体在水中的位置就很容易测出弹体速度随时间以及弹体位移的变化。图6（a）为弹体初速度分别为75.4、118.8和142.7 m/s时速度衰减与时间的关系，图6（b）为相应弹体在水中的位移与时间的关系。从图中可以看出，不同速度下柱形弹体都表现出了极强的速度衰减特性，同时弹体初速度越大，在水中的衰减越快。

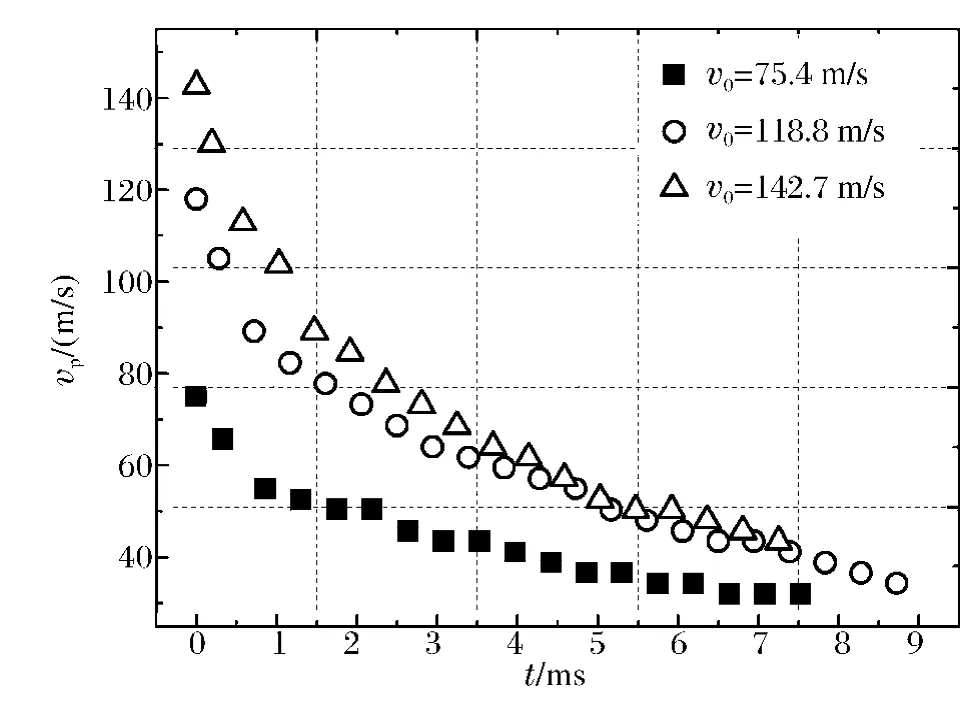
图6 （a）不同初速度下平头弹体的速度衰减与时间关系Fig.6 （a）Velocity attenuations of flat－nosed projectile

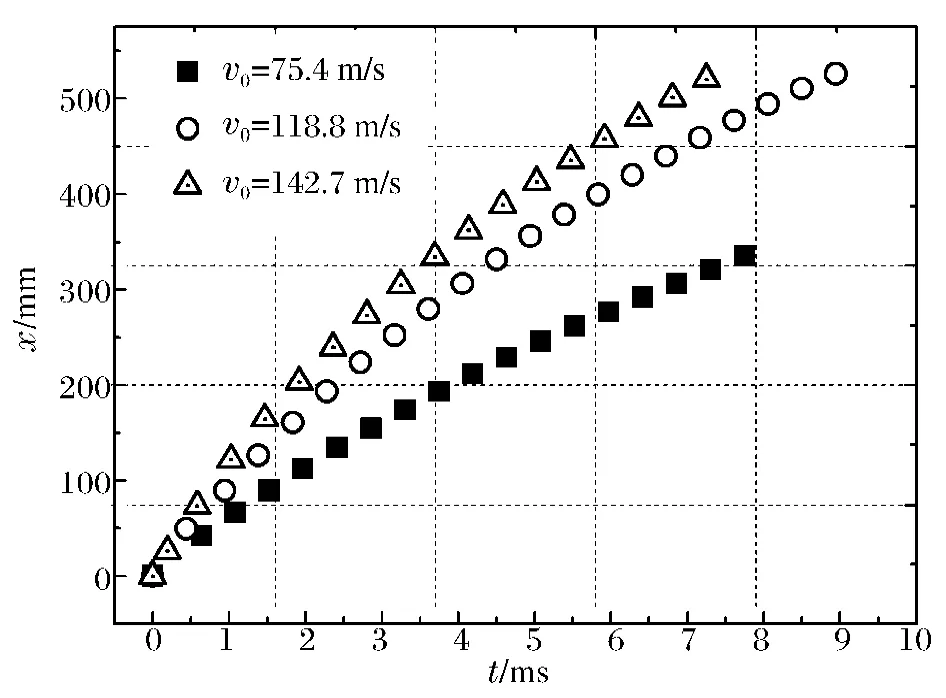
图6 （b）不同初速度下弹体位移与时间关系Fig.6 （b）Penetration distance of flat－nosed projectile

2.2.1 空化数及阻力系数

假定弹体高速入水过程中空泡内外压差不变，并认为空化数为一非定值，其规律可表示为

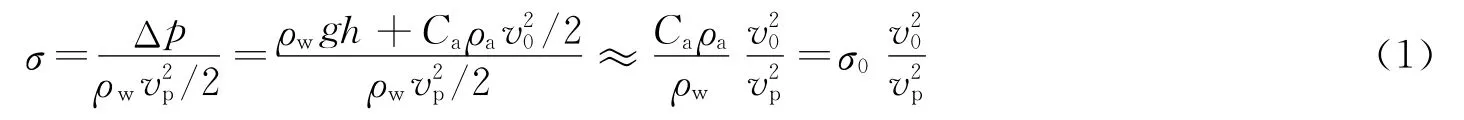
式中：Δp为空泡内外压差；Ca为气流压力降系数，Ca＝5～15［5］；σ0为初始空化数，σ0＝0.006～0.018；ρa和ρw分别为大气和水的密度；v0为弹体入水初速度，vp为弹体水中运动速度；水深h＝0.018 m，本文中忽略水深对空化数的影响。

对于柱形平头弹体，阻力系数和空化数有关系式［6］

式中：C0＝0.82～0.83。

2.2.2 弹体运动方程

忽略重力效应，根据牛顿第二定律，弹体在水中飞行有以下方程

式中：mp表示弹体质量。

根据式（1）～（2），考虑弹体速度影响，Cd（v）为非定值。由上述方程式可得到速度衰减和时间的关系式

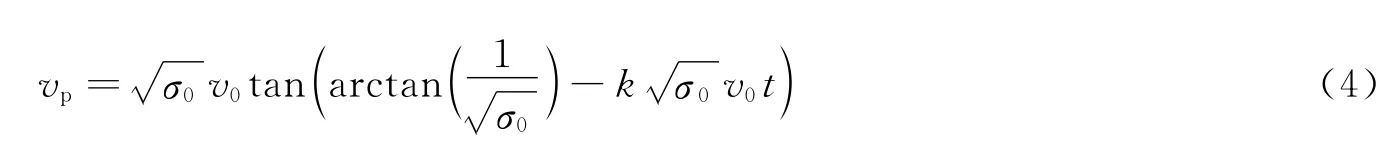
式中：衰减系数k＝ρwA0C0/2mp。

将式（4）积分，可得到弹体侵彻位移与时间的关系

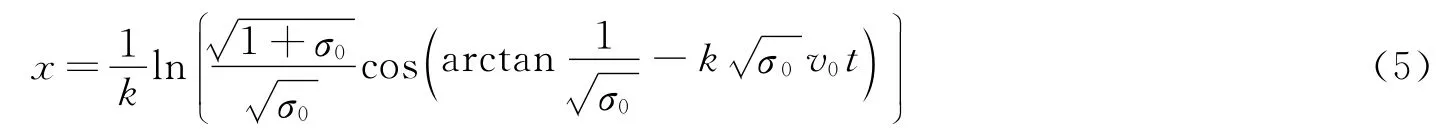
由平头弹体直径d＝12.65 mm，A0＝πr2＝125.62μm2，mp＝22.52 g，则衰减系数k＝2.29～2.31。取平均值k＝2.30，初速度为142.7 m/s的速度和弹体位移随时间变化的计算结果与实验结果比较如图7所示。可以发现，实验结果和计算结果符合很好，同时也可以看出，初始空化数对弹体速度衰减和位移随时间的变化影响很小，而衰减系数k对弹体在水中的运动则起着主导作用。

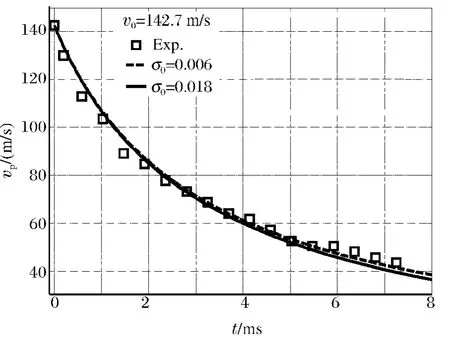
图7 （a）速度衰减的理论和实验结果对比Fig.7 （a）Comparison between experiments and analytical calculation

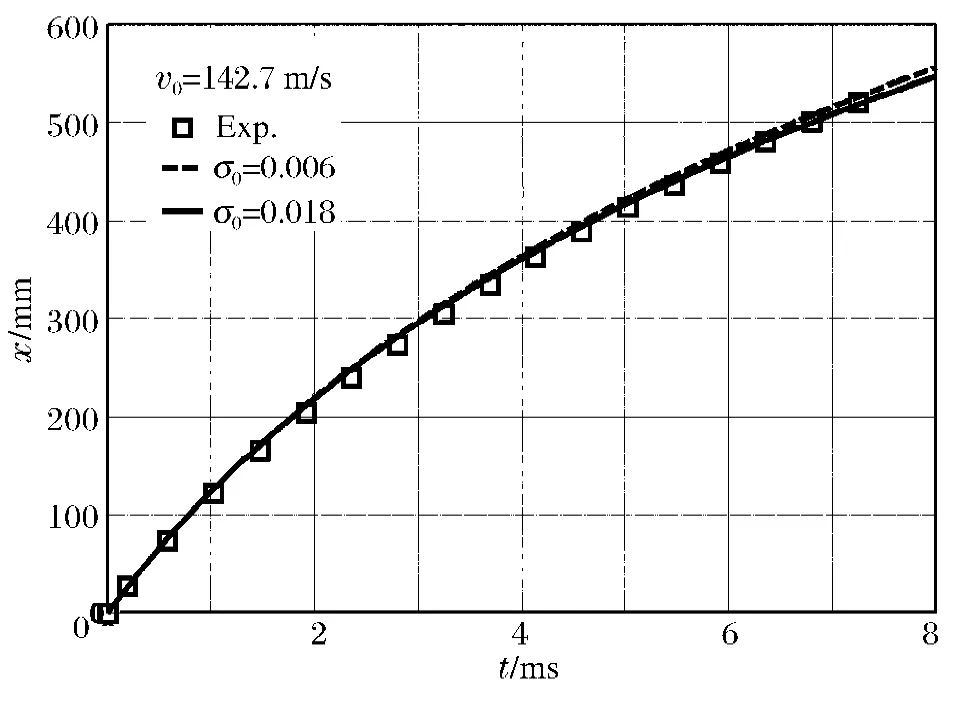
图7 （b）弹体侵彻位移的理论结果和实验结果对比Fig.7 （b）Comparison between experiments and analytical calculation for penetration distance

2.3 空泡特性分析

入水空泡形态的确定是预测入水初期水弹道的关键，但是入水问题的复杂性使得高速入水空泡的动力学问题并不能用数学方法完全解析，因此各种预测方法都不得不借助一些特定的假设来近似处理相关问题。本文中假设弹体在水中的能量流失转化为空泡周围流体的动能以及空泡内的势能。针对圆球高速垂直入水，M.Lee等［7］利用分布点源理论推出空泡周围的流体动能Ek为

式中：R表示空泡半径，N＝ln（Ra/R）为一个量纲一经验系数，表示弹体入水冲击的扰动范围，其中Ra表示入水冲击的扰动最大半径。忽略重力效应，式（6）也可以用来描述平头弹体入水的流体动能变化。对于有限长度平头弹体的空泡内势能Ep可表示为

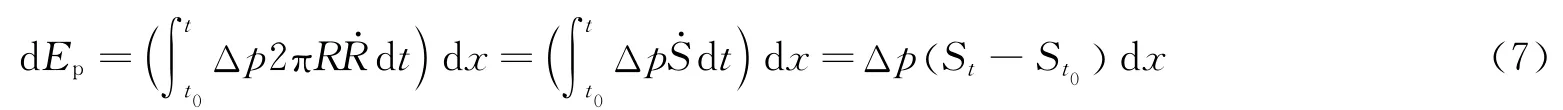
根据式（3），弹体动能Et随侵彻距离xp的变化率为

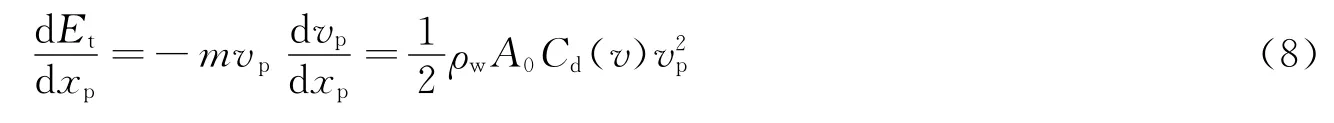
入水初期忽略速度的影响，可认为Cd为常数。根据能量守恒原理，有

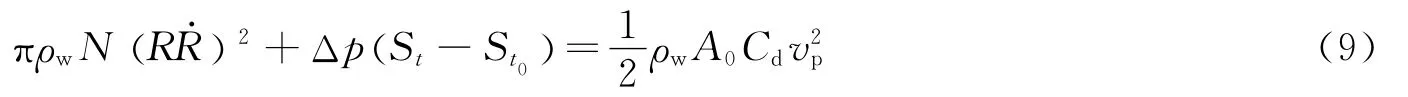
解上述方程并考虑近似关系式vp＝（x－x0）/（t－t0），可得到空泡半径随随侵彻距离变化的关系式

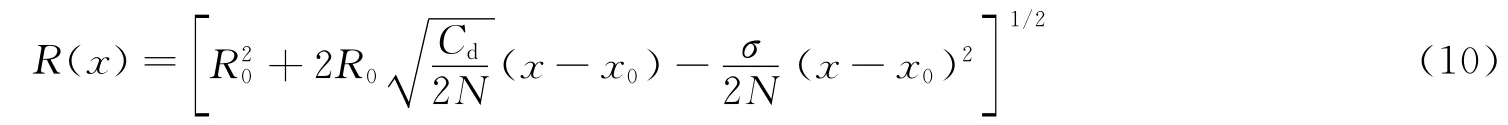
式中：x0表示t0时刻弹体的位移，R0为弹体头部半径。从式（10）可以看出，空泡尺寸与弹体头部形状、弹体阻力系数、空化数以及经验系数N有关。对于圆球垂直高速入水，G.Birkhoff等［6］推荐2.7≤N≤3.4，H.H.Shi等［8］取N＝3。但对于柱形弹体，发现N＝3时模型计算结果低估了实际的空泡尺寸，其值应小于3。

以（x－x0）作为一个变量，取Cd＝0.83，σ＝0.015，N＝2时，实验结果和模型比较如图8所示，两者符合很好，同时也可以看出不同速度下的弹体空泡尺寸是基本一致的，速度对平头弹体早期入水的空泡尺寸几乎无影响。

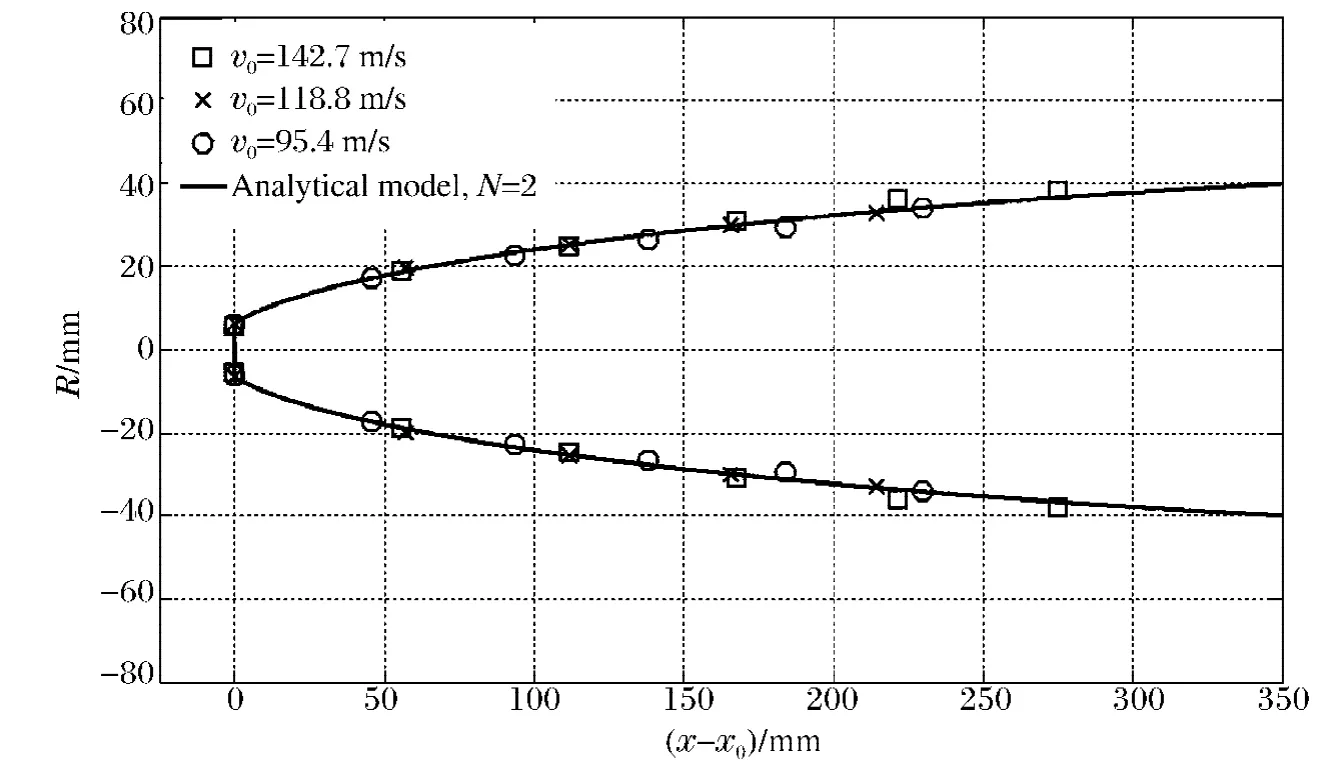
图8 空泡尺寸实验结果和模型对比Fig.8 Comparison of the cavity model with the experimental data

3 结 论

（1）弹体头部形状对弹体入水的弹道稳定性影响很大，平头柱形弹体最稳定，截卵形弹体其次，卵形弹最差，呈现出头部越锐利越容易发生偏转的特性。（2）平头弹体在水中表现出极强的速度衰减特性，同时衰减系数k很大程度上影响着弹体速度衰减规律，而初始空化数对速度衰减影响很小。入水初期，不同速度下的平头弹体的空泡形状基本相同，空泡形状由弹头形状、速度衰减系数以及空化数等所确定。通过理论分析，给出了弹体速度衰减公式以及空泡模型，实验结果和理论结果吻合较好。

［1］Waugh J G.Hydroballistics modeling［R］.AD A007529，1975.

［2］严卫生.鱼雷航行力学［M］.西安：西北工业大学出版社，2005.

［3］May A.Review of water entry theory ＆data［J］.Journal of Hydronautics，1970（4）：140－142.

［4］矶部孝.水下弹道的研究［M］.北京：国防工业出版社，1983.

［5］顾建农，张志宏，范武杰.旋转弹丸入水侵彻规律［J］.爆炸与冲击，2005，25（4）：341－349.GU Jian－nong，ZHANG Zhi－hong，FAN Wu－jie.Experimental study on the penetration law for a rotating pellet entering water［J］.Explosion and Shock Waves，2005，25（4）：341－349.

［6］Birkhoff G，Zarantonello E H，Wakes J，et al.Jets，Wakes，and Cavities［M］.New York：Academic Press，1957.

［7］Lee M，Longoria R G，Wilson D E.Cavity dynamics in high－speed water entry［J］.Physics of Fluids，1997，9（3）：540－550.

［8］Shi H H，Takami T.Some progress in the study of the water entry phenomenon［J］.Experiments in Fluids，2001，30（4）：475－477.