基于UKF 的电力系统动态状态估计

李少华，金 涛

(福州大学电气工程与自动化学院，福建福州350108)

式中，f是非线性状态转移函数，g是代数方程组，表示电力系统无源网络。计算步骤如下:

①按照式(2)，用mk-1作为状态均值获取sigma点，并且计算状态估计均值m*k:

0 引言

电力系统状态估计作为能量管理系统(EMS)的重要组成部分，发挥着重要的作用［1］。至今，世界上绝大部分电网已经在正常运行中使用了状态估计程序，其在电力系统中所得到的效果已被充分肯定。它能够利用网络接线信息和实时量测信息估计出完整、一致和可信的系统状态。从理论上讲，它就是根据数据采集和监控系统(SCADA或PMU)采集的信息，以求解非线性方程组的迭代方法求得系统状态变量(母线电压的幅值和相角)的最佳估计值。

电力系统状态估计问题已经得到了广泛的重视，国内外研究人员提出了大量算法。当然，由于一些实际原因，这些算法存在着一定的缺陷［2］，如占用内存大、估计精度不高等。近年来，由于扩展卡尔曼滤波(EKF)算法简单、容易实现、快速收敛等优点，电力系统动态状态估计主要以EKF理论为基础［3］。文献［4］将EKF算法应用到了电力系统动态状态估计中。但EKF算法在实际使用中存在明显的缺陷:一是线性化有可能产生极不稳定的滤波;二是EKF需计算雅克比矩阵的导数，这在多数情况下不是一件容易的事［5］。近年来，无迹卡尔曼滤波(UKF)算法在导航、测轨、卫星定位、导弹状态估计、语音识别等领域得到了广泛应用［6］。此算法能有效地克服EKF的不足，取得比EKF更高的估计精度，而且不用求取雅克比矩阵，计算复杂度也小于EKF法，在电力系统状态估计中应用容易实现。目前，UKF算法尚未应用在电力系统状态估计中。

1 UT变换

UT变换是一种计算一个随机变量的非线性变换的统计量的方法［5］。它是UKF算法的核心和基础。UT变换的思想是用固定数量的参数去近似一个高斯分布，这比近似任意的非线性函数或变换更容易。实现原理是在原状态分布中按某一规则取一些点，使这些点的均值和方差近似等于原状态分布的数学期望和方差;将这些点代入非线性函数中，相应得到非线性函数值点集，并求取变换后点集的均值的方差［7］。

2 UKF算法

对于非线性系统，可用下面的非线性离散时间状态转移方程和观测方程来表示:

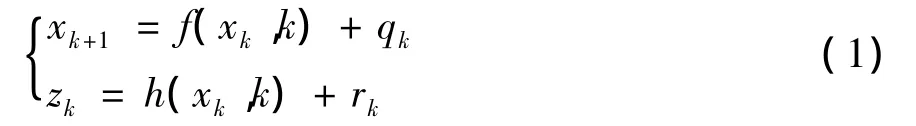
其中，xk∈Rn是在k时刻的状态变量，zk∈Rm是k时刻的量测量;f和h是非线性向量方程;qk～N(0，Qk)是k时刻的高斯白噪声，rk∈N(0，Rk)是k时刻的测量噪声;Qk和Rk是k时刻qk和rk的方差。算法步骤如下:

①预测:用mk-1作为状态均值获取sigma点，并且计算状态估计均值 ^mk和估计方差^pk:

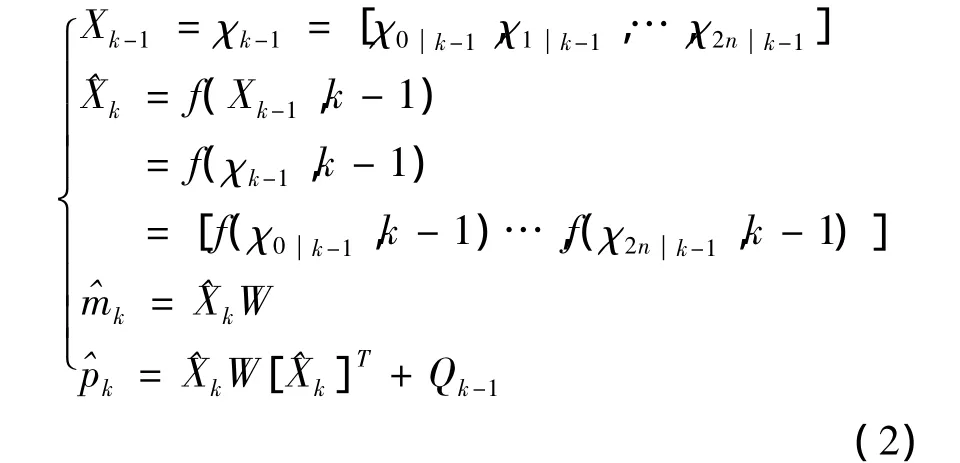
式中，W=［W0，…，W2n］T，χk-1是n×(2n+1)矩阵，χik-1是n维向量。

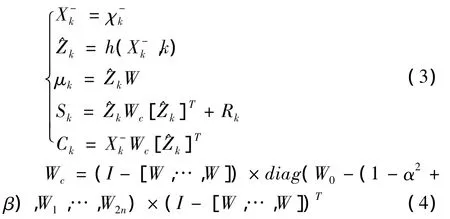
③计算滤波增益Kk和更新的状态均值mk和协方差pk:

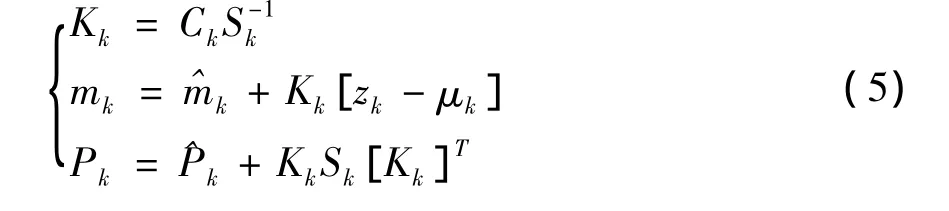
3 电力系统动态状态估计

本节将前面介绍的滤波算法运用到电力系统中。电力系统模型通常用如下微分方程组描述:

式中，f是非线性状态转移函数，g是代数方程组，表示电力系统无源网络。计算步骤如下:

①按照式(2)，用mk-1作为状态均值获取sigma点，并且计算状态估计均值m*k:

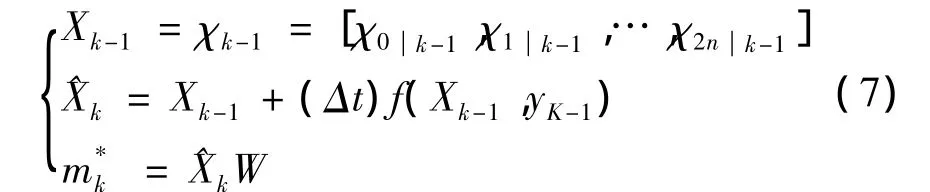
③计算状态估计均值 ^mk:

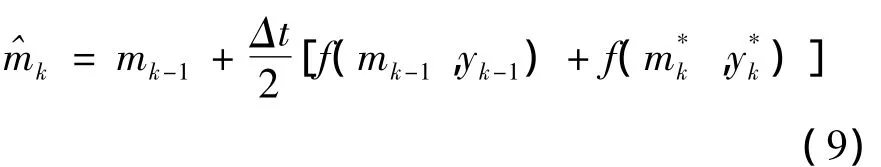
④计算^yk，解方程:

⑤按照式(3)，计算估计均值，量测量的估计均值μk和协方差Sk，以及状态量和量测量的协方差Ck:

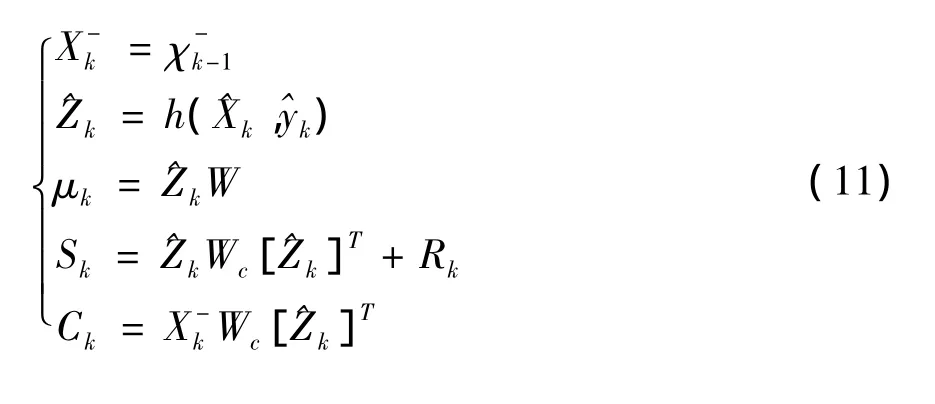
⑥计算滤波增益Kk和更新的状态均值mk及协方差pk:

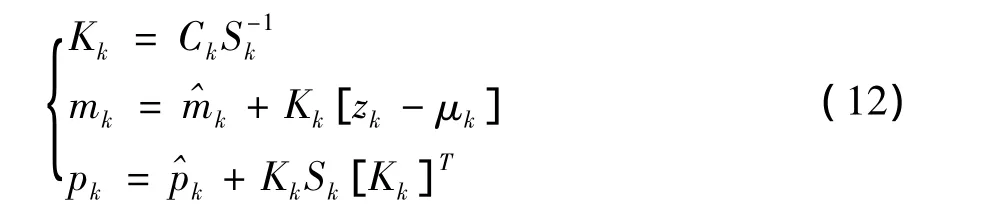
4 仿真算例

本节将UKF算法在9节点系统(如图1)中仿真、试验。在仿真系统模型中，发电机的动态用功角δ和角速度ω作为状态变量来表示。全部的状态变量是 δ1，δ2，δ3，ω1，ω2，ω3。状态转移方程如下:

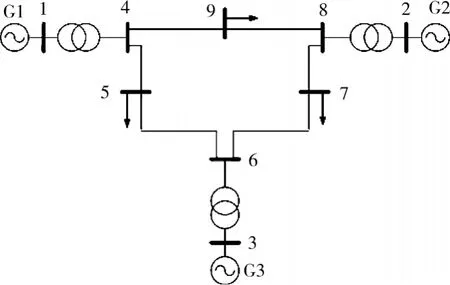
图1 9节点系统接线图

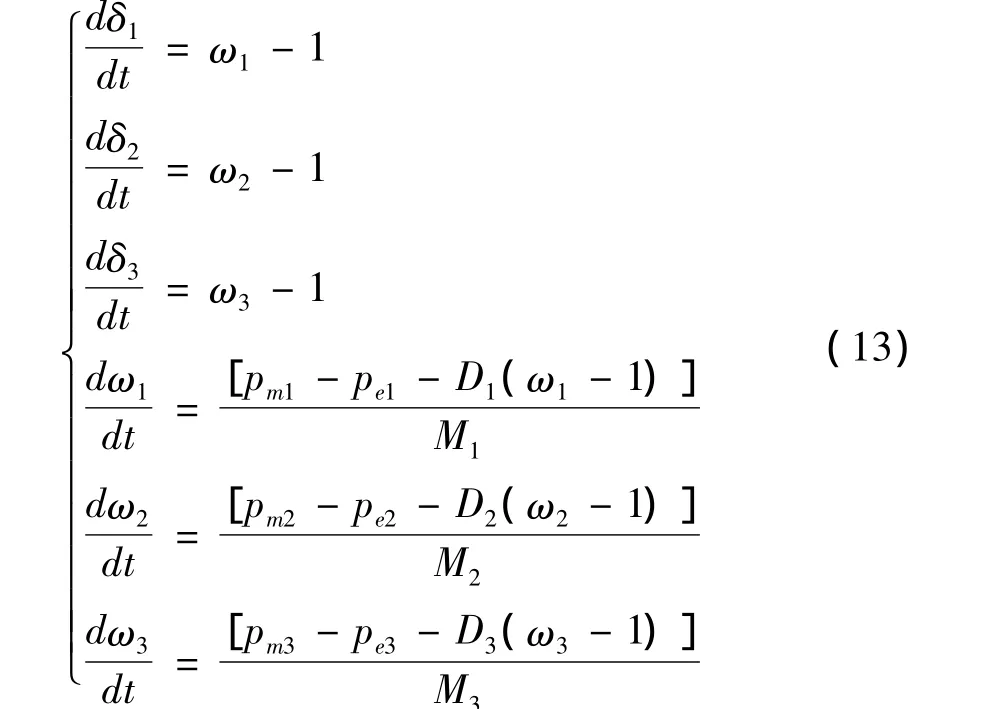
量测方程如下:

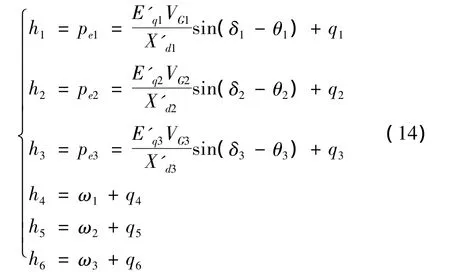
其中，VG和θ表示发电机输出电压的幅值和相角;E'q表示发电机内电压;q表示量测噪声;Pe1，Pe2，Pe3表示发电机输出电功率。发电机相关动态参数如表1所示。

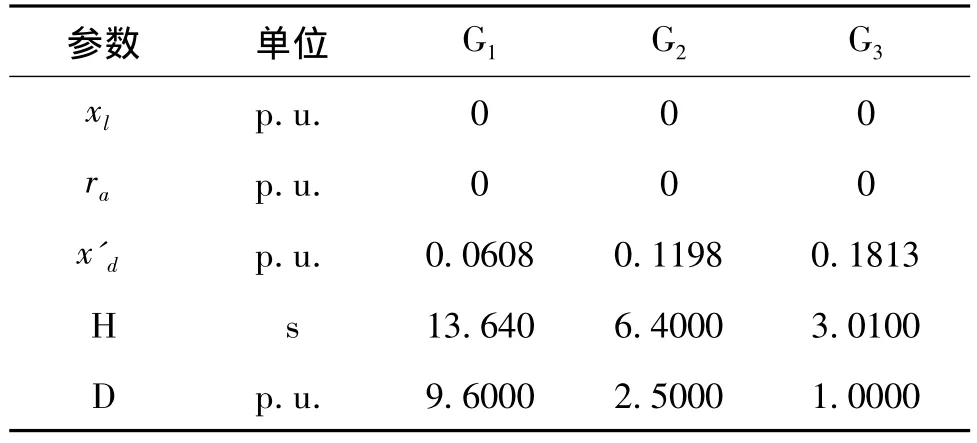
表1 发电机动态参数(Sb=100MVA)

在发电机G1的输入机械功率上设置小的干扰:t=1s时，输入机械功率以步长0.01p.u.递增，100ms之后复位。在式(7)和(9)中，Δt=0.01s。在电功率上加一个幅值为0.001p.u.的随机噪声，在转子转速上加一个幅值为0.00002p.u.的随机噪声。在上述的扰动下，测量值和真实值的对比见图2和图3，每个图中，上面是测量值的波形，下面是真实值的波形。

根据UKF算法用含噪声的量测量去估计真实值，结果见图4～5，图中实线表示真实值，虚线表示估计值。从图中可以看出:在有噪声的情况下，该算法能较好地估计真实值。然而，从图4～5也可以看出，在t=1s之前，估计值和真实值间有较大偏差。通过分析图2～5，可以得出，估计偏差是由在0＜t＜1期间测量信号信噪比较低造成的。

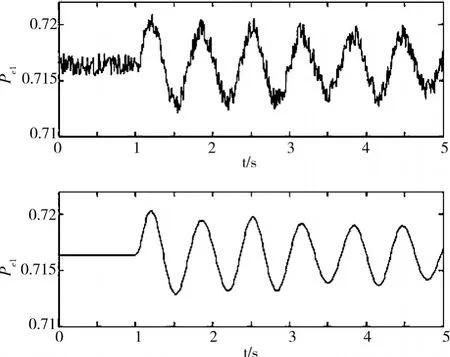
图2 Pe1的测量值和真实值

5 结语

本文介绍了一种基于UT变换的不敏卡尔曼滤波算法(UKF)，并将其应用到电力系统动态估计中，最后在9节点系统中仿真、试验。通过仿真算例可以看出，该算法可以较好地克服电力系统的非线性，而且有较高的估计精度。总之，UKF算法主要有以下优点:

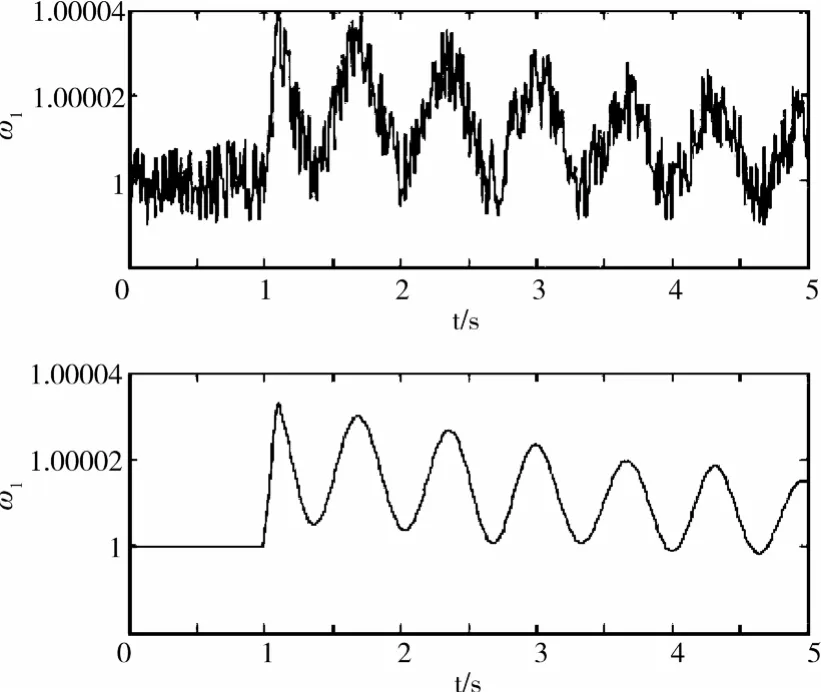
图3 ω1的测量值和真实值

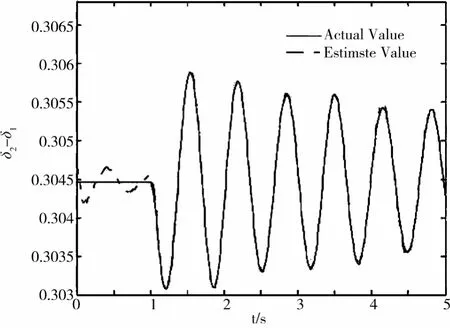
图4 δ2-δ1的真实值和估计值

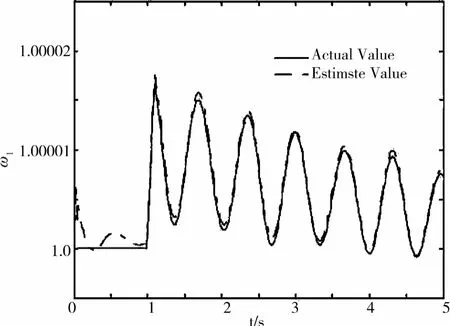
图5 ω1的真实值和估计值

(1)不需要计算雅克比矩阵来对非线性函数作近似变换，计算量小;

(2)能对所有高斯输入量的非线性函数进行近似，均值精确到三阶，方差精确到二阶;

(3)有较好的鲁棒性。

［1］李先彬.电力系统自动化［M］.北京:水利电力出版社，1986:124-125.

［2］于尔铿.电力系统状态估计［M］.北京:水利电力出版社，1985.

［3］DEBS A S，LARSON R E.A Dynamic Estimator for Tracking the State of a Power System［C］.IEEE Trans on Power Apparatus and Systems，1970，89(7):107-113.

［4］Huang Z，Schneider K，Nieplocha J.Feasibility Studies of Applying Kalman Filter Techniques to Power System Dynamic State Estimation［J］.Singapore:Proc.8th International Power Engineering Conference，2007:376-382.

［5］唐波，崔平远，陈阳舟.Unscented卡尔曼滤波在状态估计中的应用［J］.计算机仿真，2006，(4):82-120.

［6］顾飞飞，唐陇军，孙勇，等.面向事件的智能化电网调度运行日志管理系统［J］.电力系统自动化，2010，(4):1-4.

［7］周凤岐，卢晓东.最优估计理论［M］.北京:高等教育出版社，2009:149-150.