C波段高稳定陶瓷谐振振荡器设计
王红梅,温艳兵,王毅刚,马建军
(中国电子科技集团公司第55研究所,南京 210016)
1 引言
随着微波半导体技术和集成电路的飞速发展,微波设备和系统也趋向小型化、轻量化和集成化。微波陶瓷谐振振荡器(CRO)使用高Q值的陶瓷谐振器(CR)作为稳频元件,具有较好的频率及功率稳定性,且噪声低、体积小[1]。本文结合C波段CRO的电路仿真、制作从多个方面论述了实践中提高频率稳定度的方法。
2 基本原理
振荡器是由一个有源器件(二极管或三极管)和确定频率的无源谐振元件及输出匹配网络组成的,见图1。

图1 负阻振荡器等效网络[2]
从图1可以看出谐振网络、晶体管及输出网络的变化都会对振荡器频率稳定造成影响。由公式:可以看出电感L和电容C直接决定着频率,而它们又随温度、湿度、大气压力、振动等环境因素变化而变化,导致频率跟着变化。尤其是随着频率增高,电抗元件的高频损耗加大,Q值下降,所以在频率、带宽满足的前提下应尽量选择高Q值的谐振器。
3 电路设计及仿真
这里我们制作了一种C波段压控振荡器,由于在全温范围内频率稳定度指标为f±15MHz、调频线性小于1.1、总调谐带宽近200MHz,所以首先考虑到用石英谐振器、介质谐振器(DR)等固体谐振系统代替由电感、电容构成的电磁谐振系统,因为这类振荡器都是高Q值、低损耗,较易实现较高的频率稳定度、频率准确度及低相噪,且体积、耗电均很小。通过比较发现,石英谐振器的谐振频率过低,而介质谐振器在C波段体积又过大,只有陶瓷谐振器(CR)尺寸合适,为此我们在调谐回路引入了陶瓷谐振器(CR)。CR类似于硬同轴线,其中心导体的末端与同轴线的外部相连。因为CR的同轴装置是由镀银的高ε、低损耗材料制成,电磁场仅包含在同轴内部,只有很少的辐射,所以适用于高Q值、高稳定度的振荡器。CR通常工作在λ/4模式或λ/2模式。这里我们选用了TEMEX公司的CR,εr=37,工作在λ/4模式。
3.1 电路形式的选择
共基极电路易起振,调谐带宽宽;共集电极电路输出功率大、调谐带宽小,考虑到带宽,这里采用了共集电极、基极调谐、射极输出的电路,见图2。
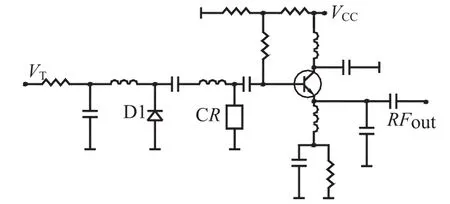
图2 电原理图
3.2 晶体管工作点的选择
晶体管的参数(输入输出阻抗等)受工作点影响很大,其结电压会随着温度升高而以一定比率降低,使结电容增大,造成频率下降,所以本例中我们除了选择高稳定的稳压块给振荡管供电外,还在稳压块引脚处并联了相差两个数量级的电容去耦来减小纹波,使相噪更好,频稳度更高;同时利用PN结在高低温下压差变化的特性,特别减小了射极下偏置电阻值,这样工作电流的改变,起到了补偿频率变化的作用,尤其是在低温下。晶体管工作在+5V,电流仅为10mA,这样也防止了因电流过大引起晶体管结温升高而导致的频漂。
3.3 回路耦合设计
负载的变化会直接反映到振荡回路中,既影响谐振频率,又使Q值变化,从而改变频率,故从振荡回路的低阻抗点输出信号可减小负载的影响。这里由于体积所限输出采用了衰减后再加放大器,而不是常规的在振荡器与负载间加隔离器,这样负载与谐振回路的耦合更弱,影响更小。谐振回路也采用了弱耦合,CR与变容管之间只用了0.2pF的片电容。
3.4 压控支路的温度补偿
这里变容管选择了1084,系常γ超突变结砷化镓变容二极管,其Q值高于硅变容二极管。由于变容管非线性,偏压低时变容管曲线斜率大,压控斜率也大,偏压高时正相反;且温度变化会使变容管接触电位和介电常数发生变化,引起结电容的变化,且呈正温度系数关系。所以我们将一只负温度系数的陶瓷电容串入变容管谐振回路,在全温范围取得较好的补偿效果。同时由于该变容管变比大,而我们只需200MHz带宽,所以对压控支路进行了分压,并在分压支路引入热敏电阻进行了温度补偿,见图3。
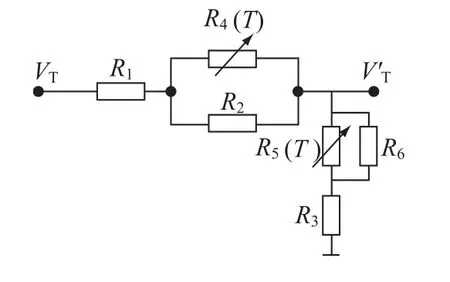
图3 压控支路
考虑到宽温范围,该补偿网络选用了双热敏电阻单T型网络,这种形式适用于二次曲线的补偿,其中R1、R2、R3为固定电阻,上偏置R4(T)为负温度系数热敏电阻,下偏置R5(T)为正温度系数热敏电阻。为防止过度补偿,这里还用了一个固定电阻R6与热敏电阻R5(T)并联,以降低R5(T)随温度变化的灵敏度。
3.5 电路仿真
仿真电路及仿真结果见图4、图5。

图4 仿真电路
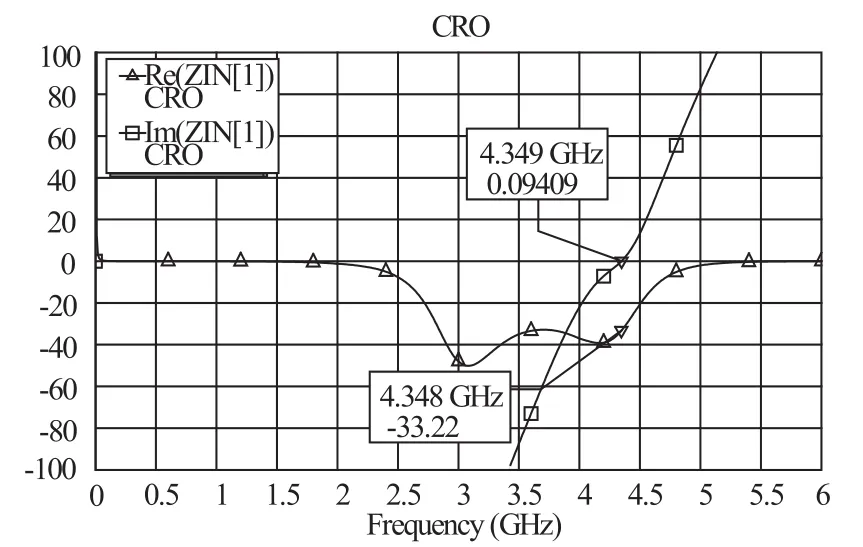
图5 仿真结果
3.6 试验结果
通过以上的分析与仿真,我们制作的C波段CRO取得了较为满意的指标,V-P、V-f特性见图6,全温范围温漂≤50×10-6/℃,带内线性≤1.1,频率稳定度≤±15MHz,带宽稳定度≤±2MHz。

图6 实测曲线
谐波抑制≥20dBc,杂波抑制≥60dBc,相噪≤-108dBc/Hz/10kHz。
4 结论
从以上分析可知,提高振荡器频率稳定度的方法就是提高振荡回路的Q值,比如选择高Q的变容管、电容、电感等元件;因Q正比于,可增加电感量;振荡管工作点的选择及电路形式也至关重要。这里再补充一点,最好在装配好一个振荡器后先进行一定时间的高温电老化,使所用元器件的状态更稳定,这样也有利于频率稳定度的提高。总之,根据产品的指标可以综合运用多种方法,以取得满意的效果。
[1] George D. Vendelin,Anthony M. Pavio,等.线性与非线性微波电路设计[M]. 北京:电子工业出版社,2010.
[2] 费元春,陈世伟,孙燕玲,等. 微波固态频率源——理论·设计·应用[M]. 北京:国防工业出版社,1994.

