水下高速射弹空泡形态与阻力特性研究

弋 辉, 张宇文, 袁绪龙, 王亚东



水下高速射弹空泡形态与阻力特性研究

弋 辉, 张宇文, 袁绪龙, 王亚东

(西北工业大学 航海学院, 陕西 西安, 710072)

试验研究射弹在水下带空泡高速运动存在诸多限制, 为了获得水下高速射弹的空泡形态和阻力系数的变化规律, 分别采用CFD仿真软件和应用基于空泡截面独立扩张原理建立的公式来研究水下高速射弹的空泡形态及阻力特性。研究结果表明, 仿真计算结果与公式计算结果吻合良好; 随着空化数的减小, 空泡的相对长度、相对直径和长细比都在增大; 在小空化数下, 空泡前部形态基本不变, 阻力系数主要为压差阻力系数, 其值基本不变。提出了水下高速射弹外形设计步骤: 公式计算初步建立模型—仿真计算修改模型—试验确立模型, 旨在为射弹的外形设计提供参考。

水下射弹; 空泡形态; CFD分析; 阻力系数

0 引言

超空泡武器是当今世界各国海军的研究热点及武器的主要发展方向。德国成功研制了超空泡反水雷射弹, 可消灭位于水下10 m深的水雷, 其发射速度达到1 000 m/s。美国在高速射弹方面处于国际领先水平, 已研制出航速达1 500 m/s的超音速射弹。美国休斯公司研制了机载快速灭雷系统, 先利用蓝绿激光探测目标, 再利用直径22 mm的高速超空泡射弹毁灭水下锚雷, 美国还研制出了一种完全在水下工作的射弹系统。

从国外发表的文章来看, 俄罗斯和乌克兰的学者基于势流理论对空化器自然空化和通气超空泡的生成, 以及空泡形状进行了理论和半经验公式研究[1-2]; 美国等西方国家主要集中在多相空化流场的数值模拟研究[3]。国内对超空化问题的研究已经取得了很大进展[4-6], 曹伟等人对射弹自然空泡形态进行了试验研究[7], 熊天红和易文俊等人对水下高速射弹的空泡形态做了数值仿真研究[8]。

本文结合国外2种研究方法, 参考国内的研究成果, 利用计算流体力学(Computational fluid dynamics, CFD)商业软件Fluent 6.3对射弹水下高速运动进行数值仿真, 使用由空泡截面独立扩张原理导出公式并经试验修正, 计算高速射弹的空泡形态及阻力系数。将仿真计算结果与公式计算结果进行对比, 研究了不同空化数下高速射弹自然超空泡的整体形态、前部形态以及阻力系数的变化规律, 为射弹弹体及尾翼的设计提供参考。根据收集到的资料, 设计了射弹光体模型, 数值仿真结果与公式计算结果吻合良好。

1 数学模型及经验公式

1.1 仿真计算的数学模型

在恒温下通过降低压力使液体破裂的过程称为空化现象。Fluent流体仿真计算软件为空化现象设计了空化模型[9], 当局部压力小于汽化压力时, 空化模型模拟了汽泡的信息。Rayleigh-Plesset方程是空化模型的主要部分, 它是由Rayleigh提出的一种针对球形空泡生成和溃灭过程的数学分析方法, 是汽泡动力学的理论基础。

对于一个半径的球形空泡, 忽略了粘性和表面张力影响的Rayleigh-Plesset方程形式为

解方程得气泡半径,随空间和时间变化。

气泡体积分数即体积含气率

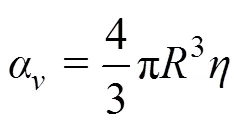
1.2 泡形计算理论及半经验公式

首先给出空化数

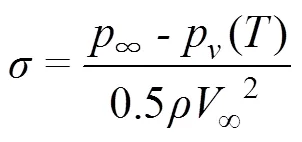
G.V.Logvinovich利用空泡截面独立扩张原理建立了空泡的截面半径公式和空泡的外形公式, 并考虑到空泡前部利用经验公式计算更准确, 得到下面的组合空泡公式[3]

2 计算结果及对比分析

2.1 射弹模型及数值计算参数设置

图1为射弹模型示意图, 弹头设计为空化效果较好的圆盘空化器, 直径为D, 射弹全长L。射弹头部有2个锥段, 第1锥段长1, 锥段过渡处直径1, 第2锥段长2, 圆柱段长3, 圆柱段直径D。射弹实体带有尾翼, 本文仅仿真计算射弹的光体模型。

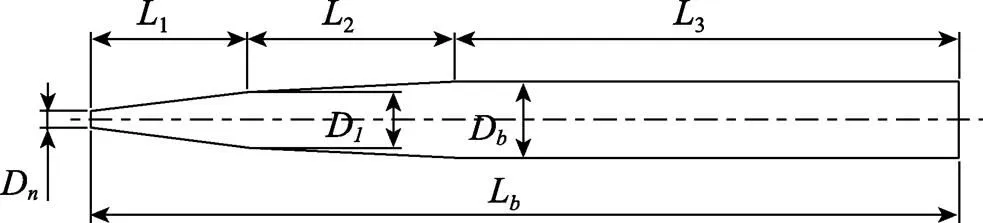
图1 水下高速射弹模型

取轴对称计算模型划分网格, 左边界为速度入口, 右边界为压力出口, 下边界为对称轴, 上边界为压力出口。考虑到空泡生成为非定常过程, 采用非定常计算方法, 采用无滑移速度的混合物模型, 近壁面采用非平衡壁面方程, 湍流模型设为分散紊流(RNG-)模型, 并选择其下的水汽不同粘性模型, 为了得到稳定的空泡形态, 压力速度耦合采用标准的simple算法, 空间离散选用默认的方法, 适当调小松弛因子。

2.2 不同空化数下空泡形态对比

射弹在水下高速运动时的空化数比水洞试验可以实现的空化数小2~4个量级, 为小空化数。射弹在1 m水深, 弹速为900 m/s, 700 m/s, 500 m/s和300 m/s时, 由式(3)可计算出对应的小空化数σ分别为2.69×10-4, 4.45×10-4, 8.72×10-4, 2.42×10-3, 此时弗劳德数很大, 不考虑重力对空泡对称性的影响[10]。

空泡的几何特征用无量纲的相对长度L/D和相对直径D/D来描述。图2描绘了空泡相对长度及相对直径随空化数的变化曲线。从图中可以看出, 1) 仿真计算所得结果与公式计算所得结果吻合良好; 2) 随着空化数的增大, 空泡的相对长度和相对直径迅速减小, 可由式(5)计算求出各空化数处的相应斜率。

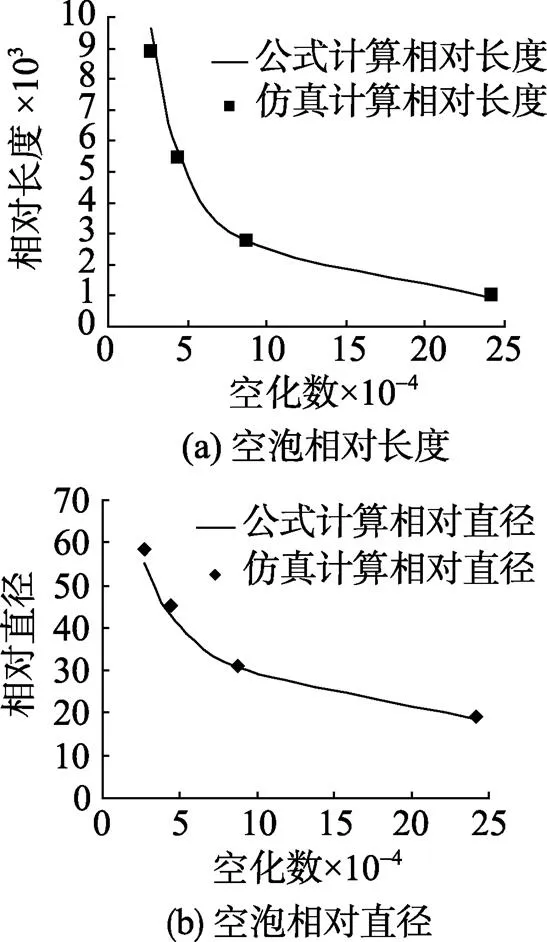
图2 不同空化数下公式计算与仿真计算空泡尺寸对比

射弹在零攻角下生成的自然超空泡近似于绕射弹轴向回转的椭球体。图3为仿真计算得到的水下高速射弹在空化数=2.42×10-3时自然超空泡的密度分布图, 从图中可以形象地看出, 射弹在水下高速运动时的空泡形态。

图3 σ=2.42×10-3时泡形密度全图与前部放大图

图4为仿真计算得到的射弹在4种小空化数下生成的自然超空泡轮廓, 表1给出了此时空泡长度和最大直径的比值即长细比的大小。从图表中可以看出: 1) 直径为一个单位长度的空化器, 在σ=2.69×10-4时生成最大直径约为60个单位长度、泡长约为9 000个单位长度的超空泡; 2) 随着空化数的增大, 长细比在减小, 空泡越来越瘦。

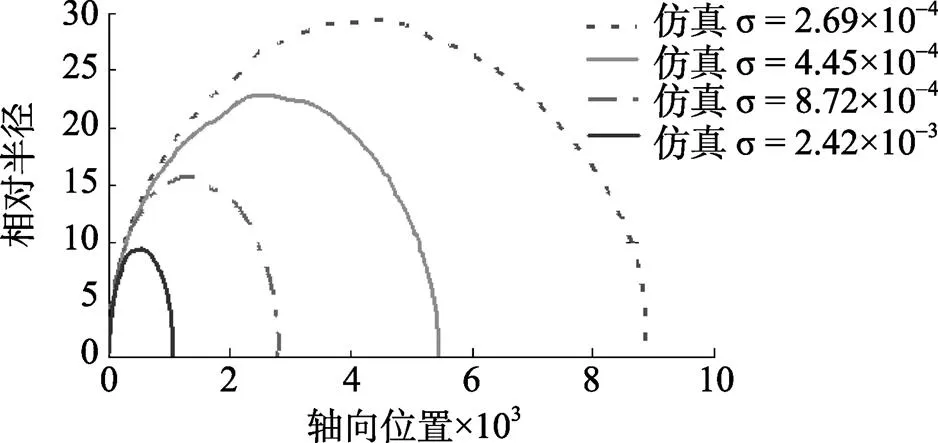
图4 不同空化数下仿真计算得到的空泡上部轮廓

表1 不同空化数下长细比对比

2.3 不同空化数下空泡前部形态

在小空化数下, 空泡细长, 最关心的是弹体附近的空泡形态随空化数的变化规律。因为此处泡形的变化将影响弹体及尾翼的沾湿状态, 从而影响射弹所受力的大小及位置分布, 对射弹运动产生影响。

图5对一组小空化数下弹体附近空泡形态曲线的仿真计算结果与公式计算结果进行对比, 从图中可以看出, 1)数值仿真结果与公式计算结果吻合良好; 2)不论数值仿真还是公式计算, 小空化数下, 随着空化数的减小, 弹体附近的空泡形态曲线没有明显的变化; 3)泡形曲线的斜率较小, 并且斜率沿轴向位置仍在减小。

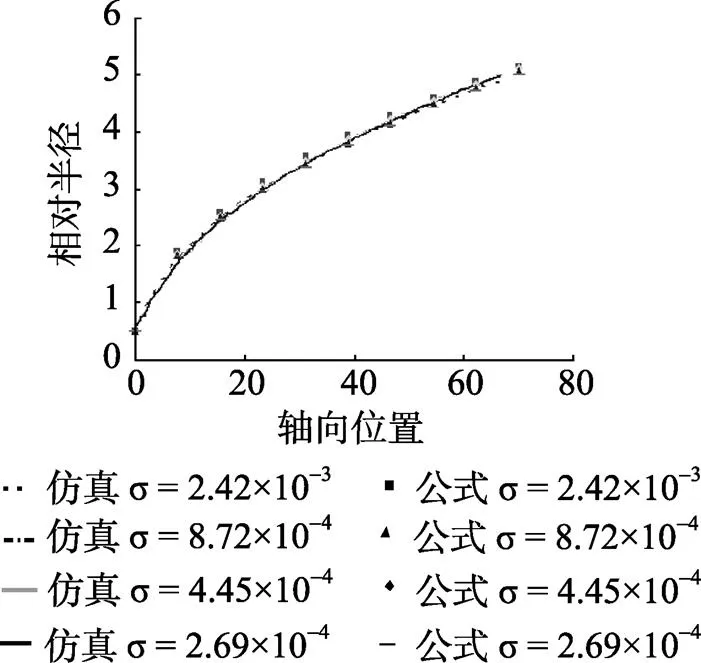
图5 不同空化数下前端泡形对比

根据以上规律可以得出, 水下高速射弹的设计思路: 应用公式计算得到某一小空化数下的空泡前部形态曲线, 然后以此曲线为参考标准结合射弹的技术要求设计射弹外形, 再根据此外形建立仿真模型, 通过数值仿真对流场作进一步研究, 然后对射弹外形提出修改意见, 最后进行试验研究。射弹外形设计包括空化器的直径、头部锥段的锥度、圆柱段的直径和长度以及尾翼的高度与位置。

2.4 不同空化数下射弹阻力系数

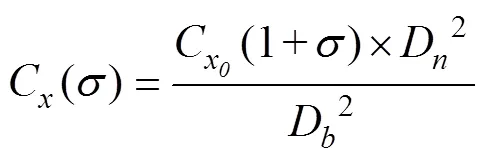
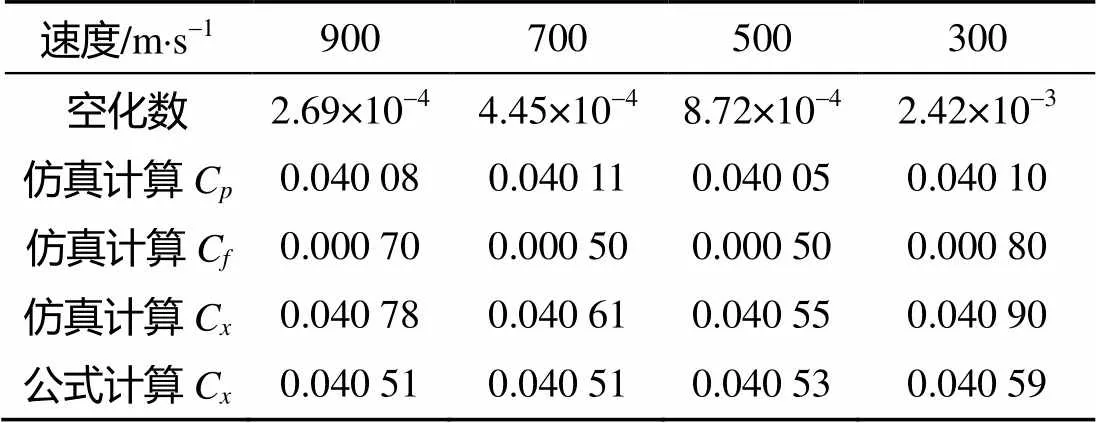
表2 不同空化数下阻力系数对比

由表2可以看出: 1) 射弹所受阻力主要为压差阻力, 粘性阻力很小, 因为在小空化数下, 空泡完全包裹弹体, 粘性阻力由汽泡产生, 而气泡的密度要比水小得多; 2) 小空化数下阻力系数不随空化数变化, 维持在某一特定值附近; 3)仿真计算和公式计算得到的阻力系数基本相等。

因此, 小空化数下, 若射弹的空化器直径和圆柱段直径已知, 可直接计算射弹的阻力系数。本文建立的射弹模型在空化数=2.42×10-3时公式计算的阻力系数为0.040 6。

进一步减小水下高速射弹的阻力系数, 需要增大射弹的圆柱段直径与圆盘空化器直径之比D/D; 适当增大射弹的相对长度L/D, 并不会对阻力系数产生影响。为了使射弹的阻力系数更小, 装载量更大, 对射弹外形设计的建议: 合适的空化器直径, 合理的头部过度锥段, 较大的射弹直径, 较长的射弹弹体, 以及与它们相匹配的尾翼。

3 结论

通过数值仿真计算及公式计算, 研究了水下高速射弹的空泡形态及阻力系数的变化规律, 得到了如下结论。

1) 小空化数下, 超空泡的相对长度和相对直径量值很大, 并且随着空化数的减小, 空泡的相对长度和相对直径快速增大, 它们的比值长细比也在增大;

2) 小空化数下, 随着空化数的减小空泡前部形态基本不变, 射弹外形应根据空泡前部形态来设计;

3) 小空化数下, 射弹所受阻力主要为压差阻力, 粘性阻力可忽略, 且射弹的阻力系数不随空化数变化, 但可以通过增大射弹圆柱段直径与空化器直径的比值来减小阻力系数, 当然, 这是受空泡前部形态约束的;

4) 空泡形态和阻力系数的仿真计算结果与公式计算结果吻合良好, 因此水下高速射弹外形设计可以参照如下步骤进行, 公式计算初步建立模型—仿真计算修改模型—试验确立模型。

[1] Savchenko Y N. Investigation of High-speed Superca- vitating Underwater Motion of Bodies[C]//Proceedings of NATO-AGARD. Ukraine: NAS-IHM, 1997.

[2] Logvinovich G V. Hydrodynamics of Flow with Free Bo- undaries[M]. Kiev: Naukova Dumka, 1969.

[3] Savchenko Y N. Supercavitation-problems and Perspecti- ves[C]//4th International Symposium on Cavitation. Cali- fornia: California Institute of Technology, 2001.

[4] 袁绪龙, 张宇文, 杨武刚. 高速超空化航行体典型空化器多相流CFD分析[J]. 弹箭与制导学报, 2005, 25(1): 53-59. Yuan Xu-long, Zhang Yu-wen, Yang Wu-gang. Multi-pha- se CFD Analysis of Typical Cavitator for High-speed Su- percavitating Underwater Vehicle[J]. Journal of Projec- tiles, Rockets Missiles and Guidance, 2005, 25(1): 53-59.

[5] 邓飞, 张宇文, 袁绪龙, 等. 水下超空泡航行体流体动力设计原理研究[J]. 西北工业大学学报, 2004, 22(6): 806-810. Deng Fei, Zhang Yu-wen, Yuan Xu-long, et al. On Hy- drodynamic Design of Underwater Supercavitating High Speed Vehicle[J]. Journal of Northwestern Polytechnical University, 2004, 22(6): 806-809.

[6] 顾建农, 高永琪, 张志宏, 等. 系列头型空泡特征及其对细长体阻力特性影响的试验研究[J]. 海军工程大学学报, 2003, 15(4): 5-9. Gu Jian-nong, Gao Yong-qi, Zhang Zhi-hong, et al. An Experiment Study of Cavities Character of Headforms and Their Influence on the Drag Character of Slender Body[J]. Journal of Naval University of Engineering, 2003, 15(4): 5-9.

[7] 曹伟, 王聪, 魏英杰, 等. 自然超空泡形态特性的射弹试验研究[J]. 工程力学, 2006, 23(12): 175-179. Cao wei, Wang Cong, Wei Ying-jie, et al. High-speed Pro- jectile Experimental Investigations on the Characteristics of Natural Supercavitation[J]. Engineering Mechanics, 2006, 23(12): 175-179.

[8] 熊天红, 易文俊. 高速射弹超空泡减阻试验研究与数值模拟分析[J]. 工程力学. 2009, 26(8): 174-178. Xiong Tian-hong, Yi Wen-jun. Experimental Research and Numerical Simulation of Supercavity Drag Reduction of a High Speed Projectile[J]. Engineering Mechanics, 2009, 26(8): 174-178.

[9] Kubota A, Kuto H, Yamaguchi H. A New Modeling of Cavitating Flows: A Numerical Study of Cavitation on a Hydro- foil Section[J]. Fluid Mech, 1992, 240: 59-96.

[10] 袁绪龙, 张宇文, 王育才, 等. 水下航行体通气超空泡非对称性研究[J]. 力学学报, 2004, 36(2): 146-150. Yuan Xu-long, Zhang Yu-wen, Wang Yu-cai, et al. On a Symmetry of Ventilated Supercavity of Underwater Vehi- cle[J]. Acta Mechanica Sinica, 2004, 36(2): 146-150.

Cavity Shape and Drag Characteristics of Underwater High-speed Projectile

YI Hui, ZHANG Yu-wen, YUAN Xu-long, WANG Ya-dong

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

Experimental study of projectile has many restrictions under underwater high-speed motion with cavity.To obtain the variation rules of cavity shape and drag characteristics of an underwater high-speed projectile, we investigated cavity shape and drag characteristics of the projectile by using computational fluid dynamics (CFD) and a formula based on the independent expansion principle of cavity sections. Conclusions are drawn that the numerical simulation agrees well with the computation of the formula; the relative length, relative diameter and slenderness ratio of cavity increase with the reduction of cavitation number; for small cavitation number, the shape of cavity front changes little, and the stable pressure difference coefficient becomes the main part of drag coefficient. We suggest the steps of shape design of the underwater high-speed projectile as follows: 1) tentative modeling by formula computing; 2) modifying model by numerical simulation; 3) establishing model by experimental method.

underwater projectile; cavity shape; computational fluid dynamics (CFD) analysis; drag coefficient

TJ630.1

A

1673-1948(2011)04-0241-05

2010-12-16;

2011-02-09.

弋 辉(1987-), 男, 在读硕士, 主要研究水中兵器流体力学, 弹道控制与传真.

(责任编辑: 陈 曦)