适用于交直流混合系统可用输电能力计算的故障排序法

孙裕佳，徐 茜

（1.华北电力大学，河北 保定 071003；2.山东电力集团公司青岛供电公司，山东 青岛 266002）

0 引言

随着电网向全国性互联电网的过渡和大容量、远距离输电的需要，以及直流输电技术的成熟和发展，高压直流输电迅速发展起来。可用输电能力作为电力系统的一个技术指标，既是反映电网输电容量的市场信号，也是衡量交易是否可行的重要指标，因此交直流混合系统可用输电能力的计算是不可或缺的。

ATC是一个时间和空间上的动态量，是一组可变且相互影响的参数的函数，取决于系统参数、运行工况和运行约束等［1］。根据对输电能力预测时间的长短，ATC计算可分为在线ATC计算和离线ATC计算；根据计算时是否将ATC视为概率随机变量，可以分为确定型ATC算法和概率型ATC算法［2］。

概率型ATC算法就是利用概率理论和数理统计分析确定ATC。将ATC视为随机变量的函数，其中随机变量用来表征系统的运行状态，描述系统运行状态的不确定性。也就是说，基于电力系统所具有的随机特征，通过模拟发输电设备的随机开断及负荷变化确定系统可能出现的运行方式，然后使用适当的优化算法求解这些运行方式下的ATC，最后综合各运行状态下的ATC值得到ATC的期望值。目前基于概率模型的ATC算法主要有以下4种：随机规划法［3］、枚举法［4］、蒙特卡罗仿真法［5-7］和Bootstrap算法［8-9］。

ATC的计算可以通过两步来完成：系统状态的确定和ATC的计算。对于系统状态的确定，如果过度地考虑不确定性因素对ATC的影响，会使计算过于保守，无法充分利用现有的输电设备资源；但是如果忽略或削弱不确定性因素的影响，会使计算过于乐观，一旦系统出现故障或过负荷等问题，很有可能会导致系统电压崩溃、失稳、解列，甚至大面积停电，对整个社会和国民经济造成不可估量的损失。所以如何恰当地考虑不确定性和随机性因素对ATC的影响，模拟电力系统的运行状态，是计算ATC时需要着重考虑的问题。在线ATC计算对计算速度要求比较高，考虑的不确定因素相对较少，需尽量准确地选择一些可能是最严重的故障进行研究，此时故障的选择和排序是确定系统状态时需要解决的主要问题。

本文推导了适合于交直流混合系统ATC计算的故障排序法，通过算例验证，该法在不影响计算精度的前提下节约计算时间，提高计算效率。

1 故障排序指标

对一种故障选择和排序算法来讲，首先要解决的问题是确立一个能反映故障对要分析系统性能影响程度的性能指标；其次，算法的精度和速度必须满足实际要求［10］。

要分析的系统性能是电网的输电能力，计算输电能力的前提是：对于一给定的运行方式，在安全约束条件下，考虑任意支路开断事故，不断增加相关区域的负荷，直到系统达到安全稳态运行极限，此时的功率传输量即为此运行方式下的最大输电能力。研究输电能力需要考虑任一支路开断事故，对于一个实际的大型电力系统，由于支路众多，因此存在着大量的支路事故方式，但并非每种事故方式都会对系统的输电能力造成影响，为了使整个分析过程在较短的时间内尽快完成，满足系统运行的需要，采用事故排序法把后果比较的事故筛选出去，只对造成严重后果的事故进行详尽分析。

传统的事故排序法采用性能指标（Performance Index，PI）对每一事故导致的后果的严重程度来进行排序［11］。但在实际运行过程中，系统中的故障总是随机发生，发生各种故障的概率也不相同，因此在对故障排序时，应该考虑故障发生概率的差别。对系统影响较严重的事故，其发生的概率不一定大；发生可能性高的事故其严重度不一定高。综合考虑事故发生的可能性及其所产生后果的严重性，定义系统事故后果期望函数［12］如下：

式中：F的物理意义表示系统中发生某一类型的事故后，该故障对系统运行所产生影响的期望函数；Γ为系统中发生某一事故的可能性函数；PI为与Γ相对应的事故发生后，该事故对系统所产生影响的严重度函数；符号⊗表示函数PI和Γ之复合，表示考虑可能性后对故障排序变化的影响，这里取2函数计算结果之积。PI与Γ的具体定义及求解如下。

2 系统性能指标函数PI

目前，国内外已出现了不少故障排序方法，这些方法评判系统事故的标准各不相同。本文以是否引起系统过负荷作为标准。

定义系统性能指标PI为反映各条线路开断后引起系统过负荷的可能性。

式中：Pl为交流线路l的有功潮流；为交流线路l的传输容量；αl为交流支路l中的并联线路数；ωl为交流线路l的权系数，反映该线路故障对系统的影响；L为网络交流支路数；Pdld为直流线路ld的有功潮流；为直流线路ld的传输容量；αdld为交流支路ld中的并联线路数；ωdld为交流线路ld的权系数，反映该线路故障对系统的影响；Ld为网络直流支路数。

ATC计算时需要选取沟点和源点，沟点和源点选择的不同将对ATC产生很大影响，尤其是对于严重故障线路的选择上，分担沟点和源点间传输电量大的线路如果故障，必定对ATC影响很大，故在故障排序时也要计入ATC源点和沟点位置的影响，这里把源点沟点位置的影响体现在线路l的权系数ωl上。 引入功率传输分布因子PTDF［13］来表征源点（节点或节点群）向沟点（节点或节点群）输送单位功率增量时线路的潮流增量，并以此作为线路权系数ωl。源点A向沟点B输送功率，线路l的权系数ωl的计算公式为：

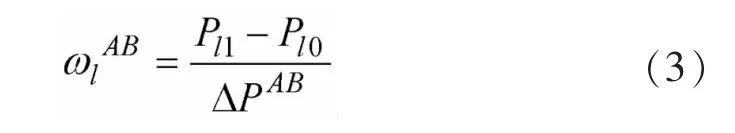
式中：ΔPAB为A、B间的功率传输量；Pl1为功率变化后线路l的潮流；Pl0为线路l的初始潮流。

由式（2）可知，当系统没有过负荷时，Pl/均不大于1，PI指标较小。当系统中有过负荷时，过负荷线路的Pl/大于1，正指数特性将使PI变得很大。因此这个指标可以概括地反映线路故障后系统过负荷的情况。通过分析PI指标对于各条线路的导纳的灵敏度就可以反映出相应线路故障对系统安全性的影响。当线路k故障时，PI指标变化量为：

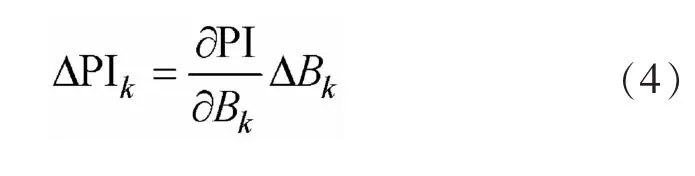
式中：ΔBk为线路k故障时，线路k的导纳变化量，由于此处考虑的线路故障方式为断线故障，即线路发生故障后便退出运行，故ΔBk即为线路导纳Bk；ΔPIk的值越大，PI值增加越多，线路k故障引起系统过负荷的可能性越大。

以下将推导利用正常情况潮流计算结果直接计算ΔPIk的公式。

交直流混合系统的直流潮流方程［14］为：

式中：B为系统交流部分节点导纳矩阵（直流线路全部断开）；θ为节点电压相位角矢量（参考节点的电压相位为零，不在其中）；P为节点注入的有功功率矢量；Pdc为从交流节点流进直流系统的有功功率矢量（不与直流系统相关联的节点，对应的分量为零）。

根据直流潮流相关知识［15］可知交流线路的潮流方程为：

式中：Pl为各交流支路潮流向量；Φ为各交流支路两端相角差向量；Bl为由各交流支路导纳组成的对角矩阵；A为网络关联矩阵；θ为节点电压相角向量。

2.1 交流线路开断

设交流线路k开断后其他各交流线路潮流变为Pl′（l=1，2，…，L，l≠k），而直流线路的有功功率不变，这时系统性能指标相应的变为

显然

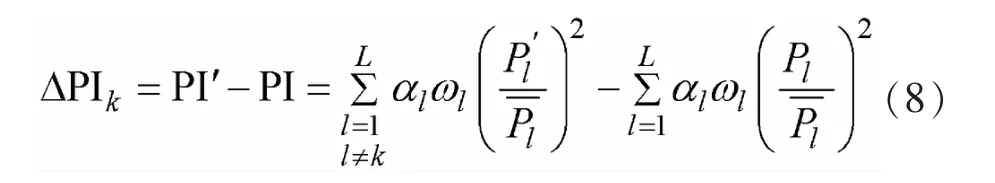
由式（6）可知Pl=Blφl，代入式（8）可得：

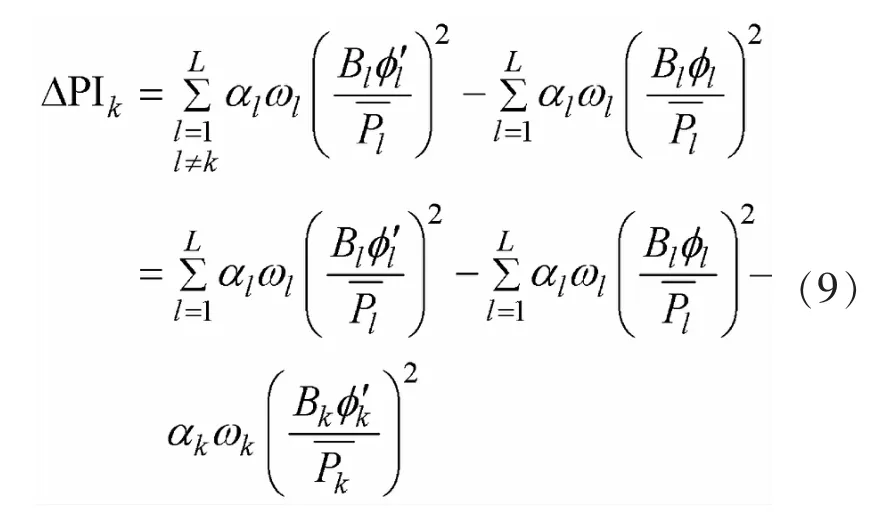
可进一步表示为

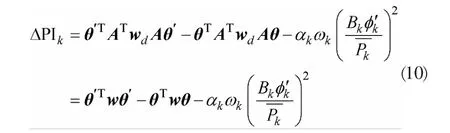
式中：θ′为线路k开断后的节点电压相角向量。

下面介绍如何求θ′。对于交流支路k（两端节点为i，j）开断，节点电纳矩阵将发生变化成为B+ΔB，其中B是支路开断前的节点电纳矩阵。如果i，j不是系统参考节点，则其中ΔB仅有4个非零元素：

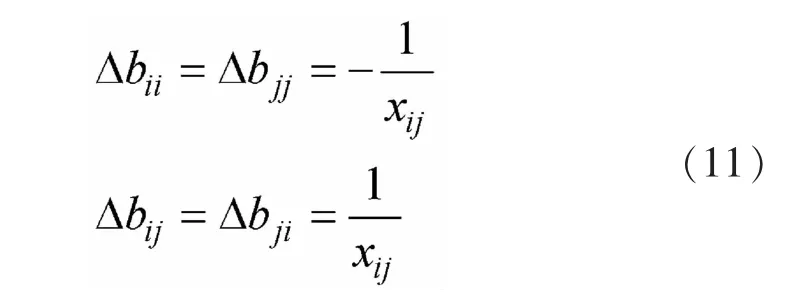
式中：xij是支路k的电抗。

由直流潮流相关知识可知

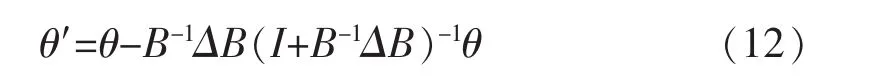
这里I是单位矩阵。

2.2 直流线路开断

对于直流线路开断，相当于Pdc出现一个增量ΔPdc，而矩阵B没有变化。增量ΔPdc取决于是单级开断还是双极开断。

对于双极开断，ΔPdc=-ΔPdc，引起的相位角增量为：

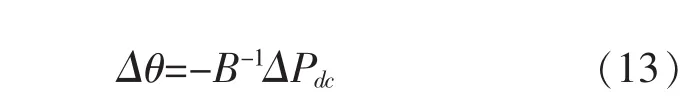
如果一极直流线路的最大输送能力Cn≥Pdc，则在单极开断后运行的另一极仍可输送开断前的直流功率Pdc，于是ΔPdc=0。若Cn≤Pdc，则直流线路少输送功率Pdc-Cn，所以ΔPdc=Cn-Pdc，由式（13）可求得由于直流线路单级开盾而引起的节点相角变化Δθ，从而求得θ′=θ+Δθ。

设直流线路k开断后各交流线路潮流变为Pl′（l=1，2，…，L），该直流线路的功率变为Pdld′，而其它直流线路的有功功率不变，这时系统性能指标相应的变为

显然

由式（6）可知Pl=Blφl，代入式（15）可得：

可进一步表示为

这些公式中的量均可通过正常情况下的潮流计算数据求得。可以利用这些公式方便地计算出各条线路开断后的ΔPI值。

3 系统状态概率函数Γ

由第1节对Γ的定义可知，Γ为系统中发生某一事故的可能性函数，即系统某一故障状态出现的概率。这里所说的故障不是通常所指的短路故障，而是指设备开断故障。对于运行中的系统，事故的发生通常是对系统中处于运行状态的设备预想其非正常地退出运行状态，即运行设备发生故障导致事故的发生，并进而引起整个系统的状态发生变化。

在开始进行安全分析后一段时间内，发生一个设备故障的概率通常比多个设备同时故障的概率大得多，故在线分析时，一般只考虑“N-1”的情况，即只考虑一个设备故障、其他设备不故障的情况［16］。

预测出设备各时刻的状态概率后，根据式（18）可推得各个时刻对应的N-1故障状态出现的概率Γk，且系统所有可能状态出现概率之和为1。

式中：Γk（t）为t时刻设备k故障的概率；Γ0（t）为t时刻系统无故障的概率。

4 算例

采用文献［17］中的改进的IEEE14节点系统作为算例。首先马尔可夫链预测出设备各时刻的状态概率；然后采用本文提出的故障排序法，筛选出对ATC影响最大的故障，确定系统状态；最后针对筛选出来的故障状态，采用内点法求解ATC。同时也用枚举法进行了系统状态确定，采用内点法求解ATC。由于只有一条直流线路，故无需进行排序。某一时刻的交流线路故障排序结果见表1，ATC计算结果见表2。

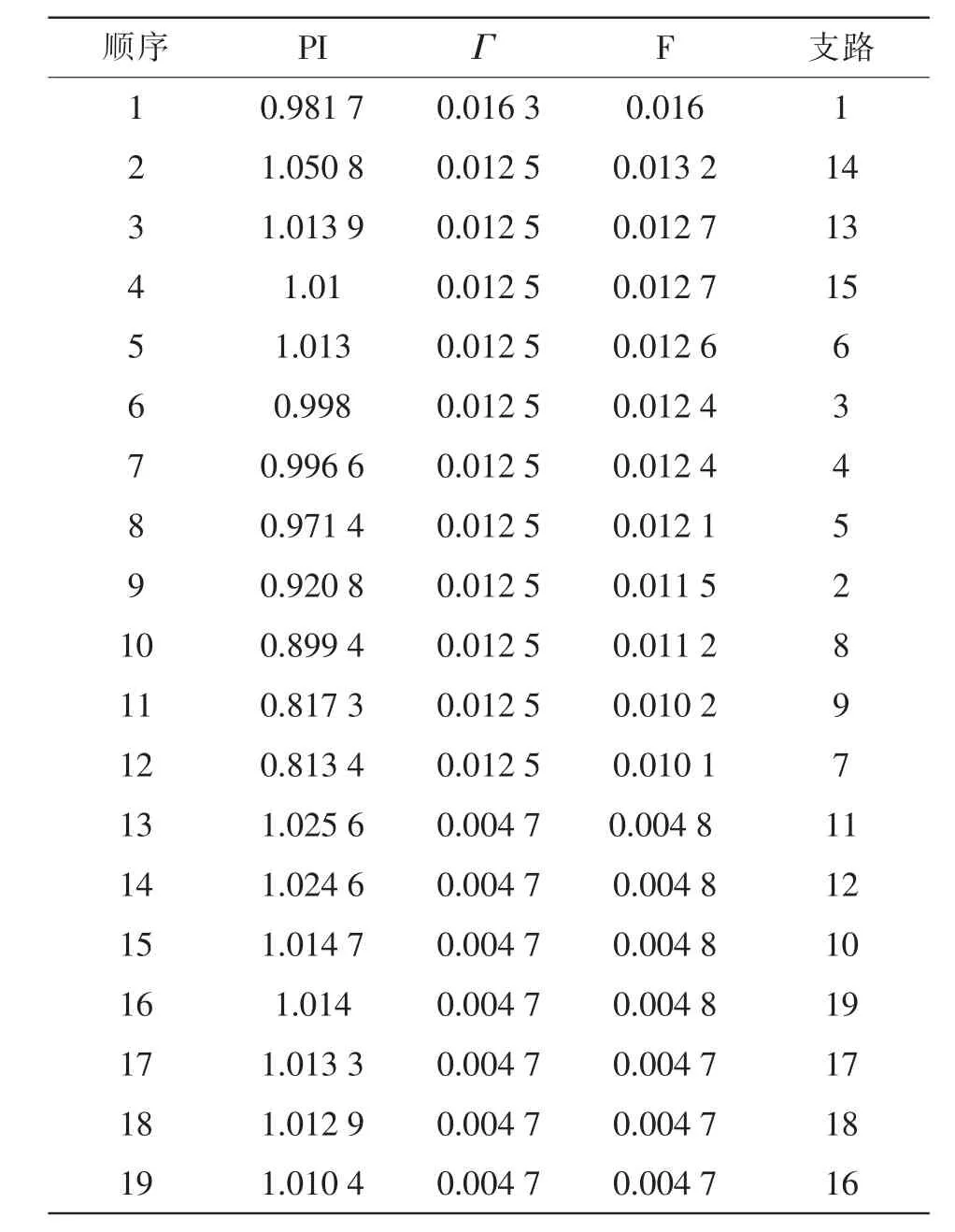
表1 交流线路故障排序结果

表2 ATC计算结果

由表2可见，故障排序法不影响ATC的计算精度，而且在计算速度上，较枚举节约了大量的时间。

5 结论

本文推导了适合于交直流混合系统ATC计算的故障排序法，该方法综合考虑了故障发生概率和故障发生后果，可以在不影响计算精度和计算速度的前提下节约计算时间，提高计算效率。