基于双电流环控制的并网逆变器设计

霍弘宇，陈伟琪

（1.广州番禺供电局 广东 广州 511400；2.广东省计量科学研究院 广东 广州 510405）

随着世界经济的发展，大部分正在使用的能源终将消耗殆尽，如何节约能源和开发利用环保、可持续的新型能源成为我们必须解决的问题。而电能回馈电网技术可以较好地实现能量的循环利用，提高终端用电效率，有效缓解电能供求矛盾等。因此，并网逆变器作为电能回馈电网的关键技术已成为学术界研究的热点。

由于并网逆变器通常采用高频PWM调制下的电流源控制，从而导致进入电网的电流中含有大量的高次谐波。为了获得无污染的入网电流，并网逆变器的输出端一般采用L和LCL两种类型的滤波器[1]。单电感L滤波器结构简单，但其高频谐波衰减特性不够理想，然而LCL滤波器滤除高次谐波效果明显，常被用于大功率、低开关频率的并网设备。但是LCL滤波器是一个三阶的谐振电路，其在提高入网电流质量的同时也提高了系统的阶数，对系统控制策略提出了更高的要求。如果采用的控制策略不妥，反而会增加电流的畸变，甚至使系统不稳定。为了抑制LCL滤波器的谐振峰对系统稳定性和电流的影响，一般情况下采用2种方法：1）在电容端串联阻尼电阻[2]。然而这会增加系统额外的功率损耗，同时也使滤波器对高频分量衰减程度降低；2）采取合适的闭环控制策略。因此如何设计控制器使系统稳定运行是必须解决的问题。引入电网电压前馈控制[3]有利于减小输出电流的稳定误差，但无法有效抑制谐波，而重复控制[4]也还存在动态响应差的缺点。

针对上述控制算法的不足，笔者提出了一种基于极点配置的电流双闭环控制策略。这种控制算法用电容电流内环来增加系统阻尼，以有效抑制谐振的发生，用入网电流外环实现对并网电流的直接控制，保证高的进网电流功率因数[5]；而用极点配置的方法选择控制参数比传统的实验法更灵活，使该控制算法更易实现。最后，本文通过Matlab仿真和实验证明了所提方法的可用性和正确性。

1 并网逆变器的数学模型

1.1 并网逆变器的拓扑结构

三相并网逆变器的主电路拓扑结构如图1所示。图中idc代表直流输入，T1～T6代表三相逆变桥的6个IGBT开关管，R代表滤波电感内阻和由每相桥臂上、下管互锁死区所引起的电压损失，L1、C、L2组成三阶 LCL滤波器。

1.2 LCL滤波器与单电感滤波器的性能比较

图1 三相并网逆变器拓扑结构Fig.1 Topology structure of the three-phase grid-connected inverter

由于LCL滤波器相对传统的单电感和LC滤波器具有更好的高频谐波衰减特性，因此选择LCL结构的滤波网络来实现逆变器与电网之间的连接。设Z1为滤波器逆变侧阻抗，Z2为电网侧等效阻抗，Z3为滤波电容阻抗，则滤波网络的等效传递函数为：

忽略电感与电容的寄生参数，可推导出：

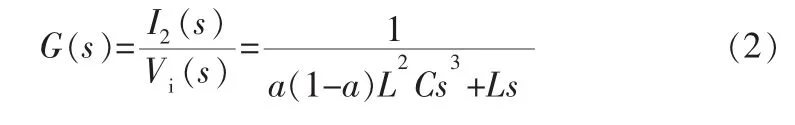
其中L为LCL滤波器的电感，L=L1+L2，C为滤波电容，且α=L1/L，根据式（2）选取不同的滤波参数，可得到一组滤波器U-I传递函数Bode图，如图2所示。图中曲线1所选的参数为C=12 μF，α=0.9；曲线 2 所选的参数为 C=0；曲线 3 所选的参数为 C=12 μF，α=0.25；曲线 4 所选的参数为 C=12 μF，α=0.5。

图2 LCL滤波器的传递函数Bode图Fig.2 Bode diagram of the LCL filter

由图可知，在低频段，LCL滤波器与单电感滤波器的特性基本相同；而在高频段，单电感滤波器的增益衰减速度维持不变，LCL滤波器则具有较大的衰减，表明其对开关频率谐波具有更大的抑制能力。但在高频与低频段的连接点及其附近，LCL滤波器出现幅值增益尖峰，这将对系统的稳定性造成很大影响。

1.3 并网逆变器状态空间数学模型的建立

逆变器状态空间模型[6]的具体形式与所选择的状态变量有关，这里选择 L1电感电流 i1a、i1b、i1c，电容电压 Vca、Vcb、Vcc和并网电流i2a、i2b、i2c为状态变量，由此可得并网逆变器在ABC静止坐标下的状态方程。经过ABC-αβ变换后，整理可得在αβ坐标系下的状态空间方程如式（3）所示。由式（3）可知，α轴上的状态变量 i1α、i2α、icα和 β 轴上的状态 变量 i1β、i2β、icβ没有耦合关系，并且α轴或β轴上状态变量的内部关系与单相PWM逆变器的状态方程是一致的。因此，经过ABC-αβ坐标变换后，平衡三相PWM逆变器可等效为两个相互独立的单相PWM逆变器。因此，有关三相逆变器的研究可基于单相逆变器展开，这大大方便了三相逆变器控制策略的研究。

由单相的LCL滤波器可推得并网输出电流I2同并网逆变器桥臂电压V和电网电压Us之间的传递函数为：

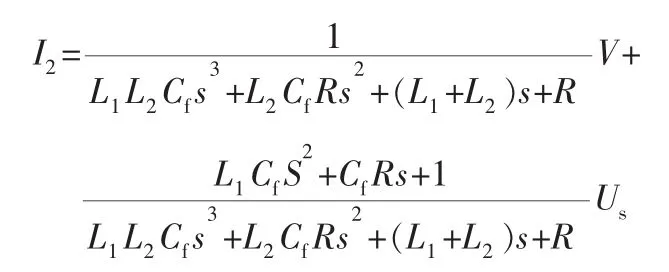
2 电流双环控制

2.1 电流双环控制原理分析

在并网逆变系统中，电容电流与电网电流的3次微分成比例关系，所以采用并网电流和电容电流[7]的双闭环控制可以有效地补偿网侧电流畸变，在选择合适的内外环控制器参数下完全能够使系统稳定运行。而在大多数文献中，控制器参数的获得都是通过尝试法，这种方法在实际应用中可行性不强。为此，笔者提出了一种通过极点配置选取参数的方法。

逆变器控制系统的结构框图如下：

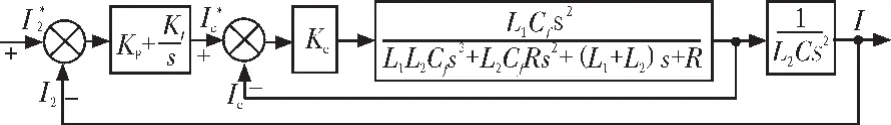
图3 逆变器控制系统结构框图Fig.3 Block diagram of the inverter control system

由此可得该系统的闭环传递函数为：

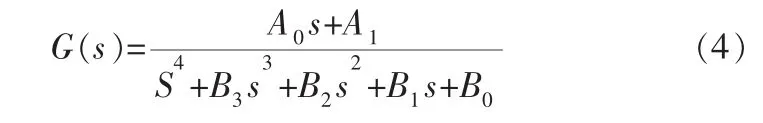
其闭环系统的特征方程为：

其中 A0=KpKc/L1L2C， B1=（R+KpKc）/L1L2C

B0=KiKc/L1L2C， A1=KiKc/L1L2C

B2=（L1+L2）/L1L2C， B3=（R+Kc）/L1

由式（4）可知，带有LCL滤波器的逆变器为典型的四阶线性系统。

2.2 极点配置方法

控制系统的动态性能和稳定性主要取决于闭环系统的主导极点在根平面上的分布。因此在极点配置时，往往是先确定一组期望的闭环极点，或者根据时域指标转换成一组等价的期望极点，再通过选择反馈增益矩阵，将闭环系统的极点恰好配置在根平面上所期望的位置，以获得所希望的系统性能。

假设四阶双环控制系统的期望闭环极点为：

可得期望的闭环特征方程为：

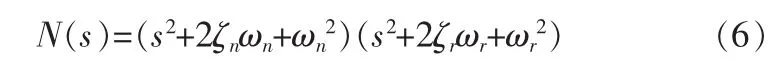
假设极点S1、2为双环控制系统的一对共轭主导闭环极点，控制系统的性能主要由主导极点决定，ωr、ζr分别为主导极点的固有频率和阻尼比。设极点S3、4与虚轴的距离是S1、2的m倍。由此可得如下关系式：

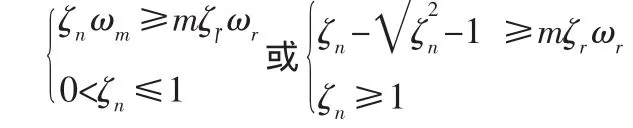
比较式（5）和式（6）可得：

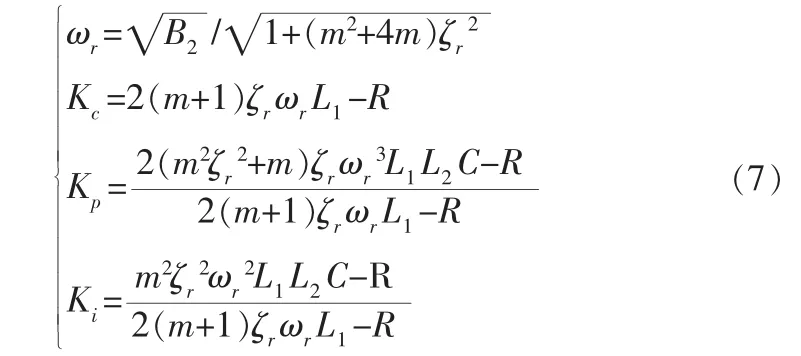
根据式（7），在给定ζr和m的情况下，可以求出唯一一组控制参数。

3 闭环系统性能分析及实验仿真

3.1 系统仿真

图4为ζr=0.6，m取不同值时的闭环系统Bode图。当m值减小时，闭环系统带宽越宽，幅值和相位差越小，但谐振频率和峰值也就越高，相应的高频抑制能力受到限制；而m值增大时，闭环系统性能恰好相反。因此在极点配置时，需选择合适的ζr和m值。

通过闭环系统 Bode图的分析，这里设定 ζr=0.6，m=4，并选取系统参数 UDC=900 V，L1=0.8 mH，L2=1 mH，C2=30 μF，R=0.4 Ω，由公式（7）可计算出 Kp=0.21，Ki=292.26，Kc=11.36。 在Simulink中搭建系统结构，利用计算所得的控制参数，可得单相网侧电流和并网电压的仿真波形如图5所示。此时，系统网侧电压、电流反相（负组特性），功率因数接近-1，网侧电流畸变小，系统稳定。

图4 闭环控制系统Bode图Fig.4 Bode diagram of the closed-loop control system

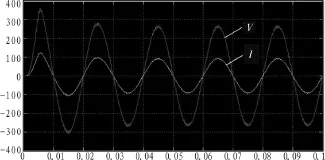
图5 仿真波形（V为电网电压，I为网侧电流）Fig.5 Simulation waveform of the grid voltage and current

3.2 实验验证

Matlab的仿真结果验证了笔者提出的应用于再生能源回馈电网系统的逆变器方案的可行性和有效性，并给实验电路提供了优化的参数。在此基础上，研制一台基于DSP的三相PWM并网逆变器，对该逆变器方案进行了实验验证。在实验中采用TI公司的2000系列DSP芯片TMS320F280035，该芯片能产生高精度的PWM波形，速度快，实时性好。系统的输出电流和电压波形如图6所示，其中通道1代表电压波形，通道2代表电流波形。

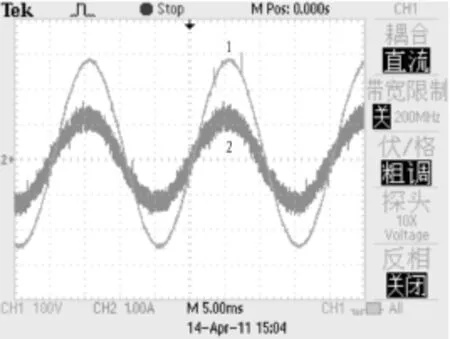
图6 实验波形Fig.6 The experimental waveform of system

4 结 论

笔者首先通过对三相并网逆变器结构的分析，建立了系统的状态空间数学模型。其次，分析了基于电网电流和电容电流的电流双环控制，重点介绍了基于极点配置的控制参数选择方法。最后，通过仿真和实验验证该控制策略的正确性。

[1]张崇巍，张兴.PWM整流器及其控制[M].北京：机械工业出版社.2003.

[2]Halimi B，Dahono P A.A current control method for phasecontrolled rectifier that has an LCL Filter[C]//Proceedings of 2011 4th IEEE International Conference on Power Electronics and Drive Systems，Indonesia，2001（1）：20-25.

[3]王兆安，杨君.谐波抑制和无功功率补偿[M].北京：机械工业出版社，2003.

[4]沈国桥，徐德鸿.LCL滤波并网逆变器的分裂电容法电流控制[J].中国电机工程学报，2008，28（18）：36-41.SHEN Guo-qiao，XU De-hong.Current control for gridconnected inverters by splitting the capacitor of LCL filter[J].Proceedings of the CSEE，2008，28（18）：36-41.

[5]Liserre M，Blaabjerg F，Hansen S.Design and control of an LCL-filter-based three-phase active rectifier[J].IEEE Transactions on Industry Application，2005，41（5）：1281-1291.

[6]赵清林，郭小强，邬伟扬.单相逆变器并网控制技术研究[J].中国电机工程学报，2007，27（16）：60-64.ZHAO Qing-lin，GUO Xiao-qiang，WU Wei-yang.Research on control strategy for singel-phase grid-connected inverter[J].Proceedings of the CSEE，2007，27（16）：60-64.

[7]梁超辉，刘邦银，段善旭.基于滤波电容电流补偿的并网逆变器控制[J].电力电子技术，2008，42（8）：13-15.LIANG Chao-hui，LIU Bang-yin，DUAN Shan-xu.Control of grid-connected inverter based on filter capacitor current compensation[J].Power Electronics，2008，42（8）：13-15.