一种超混沌自动转换系统的设计与分析
伍俊杰,孙友林,陈 君
(广东工业大学 自动化学院,广东 广州 510006)
与混沌系统相比,超混沌系统具有2个或2个以上的正Lyapunov指数,相轨在更多方向上分离,其动力学行为更为复杂。复杂的超混沌系统集可提高混沌保密通信和混沌信息加密的安全性。因此,对超混沌系统的研究将是保密通信安全领域中混沌应用的一个重要课题[1-7]。
由于混沌系统具有对初始值高度敏感的特性,现在,混沌系统的保密安全性利用越来越多,越来越多的人也开始研究一些方法去生成混沌系统。但是,超混沌系统的生成仍是一个关键技术,迄今仍没有一个生成超混沌系统的系统方法[2-3],但越来越多的研究人员开始对超混沌系统进行研究,希望通过对超混沌系统的研究,合得通信保密领域的安全性能进一步加强。
提出了一种实现超混沌的自动转换系统,将一种超混沌系统利用开关函数自动转换为另外一种超混沌系统,用matlab对超混沌系统进行仿真,对超混沌系统进行参数设置,通过观察超混沌系统吸引子相图和Lyapunov图并进行分析研究,理论分析结果与仿真结果完全一致。
1 超混沌系统自动转换模型构造及分析
文献[4]中构造的超混沌系统:
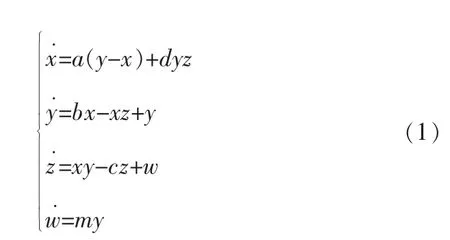
当系统参数 a=15,b=50,c=6,d=0.4,m=17 时,系统(1)处于超混沌状态[4],计算机仿真表明,此时系统(1)的Lyapunov指数为:LE1=1.383 5,LE2=0.119 6,LE3=-0.284 7,LE4=-21.218 4,其超混沌吸引子的计算机仿真图如图1所示。
在系统(1)中,把第3个方程中的非线性项xy变成x2,其他不变,得到如下新的超混沌系统:方程的维数不小于4;系统方程至

少有3个非线性乘积项。在与系统(1)相同的参数条件下,系

图1 系统(1)各平面吸引子相图Fig.1 System (1) phase diagrams of the plane attractors
产生超混沌吸引子的几个必要条件:具有耗散结构,即统(2)△V=-a+1-c+m=-15+1-6=-20<0,且系统维数为 4,有 3个非线性项,故满足超混沌的几个必要条件,故系统(2)有可能导致超混沌产生。若系统(2)Lyapunov指数有两个为正,则能产生超混沌。计算机仿真表明,系统(2)的Lyapunov指数为:LE1=2.602 2,LE2=2.483 5,LE3=-2.521 2,LE4=-22.503 5,其超混沌吸引子的计算机仿真如图2所示。
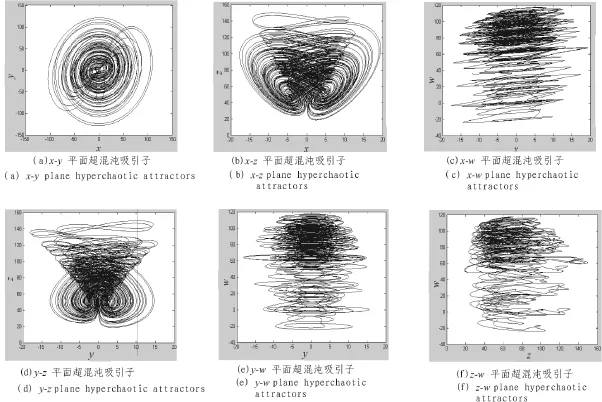
图2 系统(2)各平面吸引子相图Fig.2 System (2) phase diagrams of the plane attractors
文献[5]中,利用1个开关函数实现了由2个超混沌系统组成的自动切换超混沌系统,文献[5]使用的开关函数为:
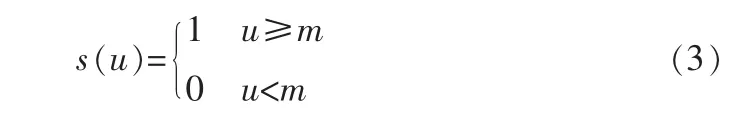
本文构造的开关函数为:

系统(1)到系统(2)的超混沌自动转换系统如下:
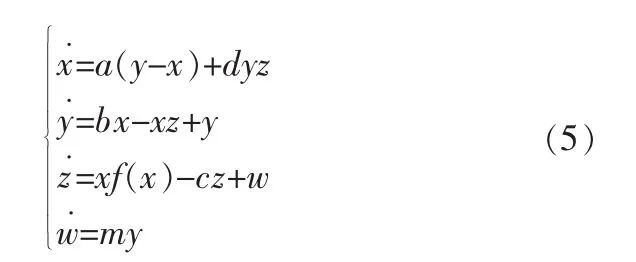
在系统(1)和系统(2)相同的参数条件下,经计算机仿真表明,系统(5)的 Lyapunov 指数为:LE1=2.425 6,LE2=2.417 8,LE3=-3.247 8,LE4=-22.502 6。 此时,系统(5)也处于超混沌状态。 当 x≥0,系统(5)运行子系统(2)状态;当 x<0,系统(5)运行子系统(1)状态。因此,在整个混沌系统过种中,即t→∞过程中,系统(5)一直在子系统(1)与子系统(2)之间随机转换[5]。
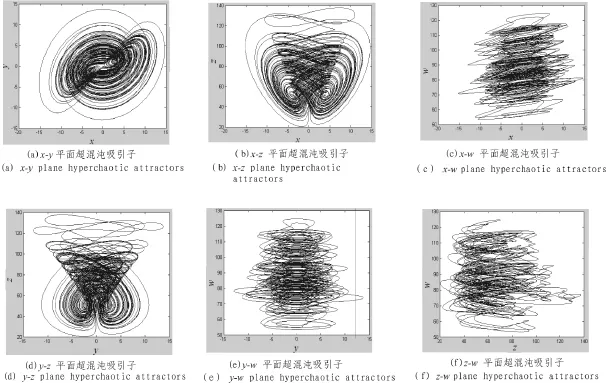
图3 自动转换系统各平面吸引子相图Fig.3 Automatic conversion system phase diagrams of the plane attractors
2 Lyapunov指数谱及其分析
系统(2)的Jacobia矩阵为:
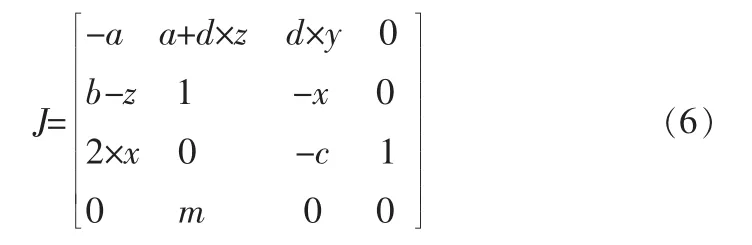
系统(5)的Jacobia矩阵为:
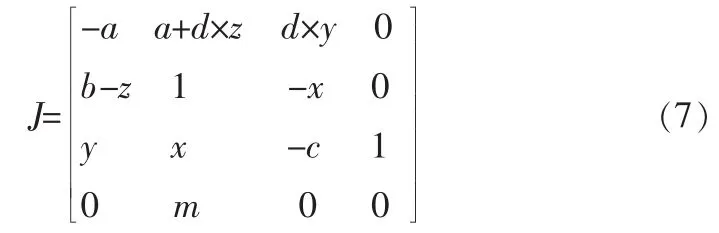
经过计算机仿真,系统(2)的Lyapunov指数如图4,系统(5)的 Lyapunov 指数如图 5。 其中系统(2)和系统(5)都有两个正的 Lyapunov 指数(LE1,LE2),有两个负的 Lyapunov 指数(LE3,LE4)。
利用Lyapunov指数进行分析时,对于平衡点有LE4 图4 系统(2)Lyapunov指数Fig.4 Lyapunov index of system (2) 图5 系统(5)Lyapunov指数Fig.5 Lyapunov index of system (5) 构造了一个新的超混沌系统,它与已有的超混沌系统构成了一个自动转换超混沌系统,分析了新的超混沌系统与自动转换超混沌系统的Lyapunov图及吸引子相图,将这个超混沌自动转换系统应用于保密通信,可以增强通信的安全性,使得系统间的切换更加灵活,从而使通信系统更难以被破解。因此这种可以自动切换的超混沌系统具有潜在的应用前景。 [1]王忠林,姚福安,李祥峰.基于PFGA的一个超混沌系统设计与电路实现[J].山东大学学报:理学版,2008,43(12):0093-0096. WANG Zhong-lin, YAO Fu-an, LI Xiang-feng.Design and realization of a hyperchaotic system based FPGA[J].Journal of Shandong University:Science editon, 2008, 43(12):0093-0096. [2]CHEN Guan-rong,UETA T.Yet another chaotic attractor[J].Int Bifurc Chaos, 1999(9):1465-1466. [3]LV Jin-hu,CHEN Guan-rong.A new chaotic attractor coined[J].Int Bifurc Chaos, 2002(12):659-661. [4]罗小华,李元彬,罗明伟,等.一种新的四维二次超混沌系统及其电路实现[J].微电子学,2009,39(3):0398-0401.LUO Xiao-hua, LI Yuan-bin, LUO Ming-wei, et al.A new 4-D quadratic chaos system and its circuit implementation[J].Microelectronics,2009, 39(3):0398-0401. [5]WANG Guang-yi,HE Hai-lian.A new Rǒsslor hyperchaotic system and its realization with systematic circuit parameter design[J].Chinese Physics B,2008,17(11):4014-4021. [6]刘扬正,姜长生,林长圣,等.四维切换超混沌系统[J].物理学报,2007,56(9):5131-5135.LIU Yang-zheng, JIANG Chang-sheng, LIN Chang-sheng,et al.Four-dimensional switchable hyperchaotic system[J].Chinese Physics, 2007, 56(9):5131-5135. [7]禹思敏,吕金虎.高阶蔡氏电路及其FPGA实现[C]//第26届中国控制会议论文集,2007:409-413. [8]周武杰,禹思敏.基于现场可编程门阵列技术的混沌数字通信系统—设计与实现[J].物理学报,2009,58(1):0113-0119.ZHOU Wu-jie,YU Si-min.Chaotic digital communication system based on field programmable gate array technology—Design and implementation[J].Chinese Physics,2009,58(01):0113-0119. [9]王杰智,陈增强,袁著祉.一个新的混沌系统及其性质研究[J].物理学报,2006,55(08):3956-3963.WANG Jie-zhi, CHEN Zeng-qiang, YUAN Zhu-zhi.A new chaos system and character study[J].Chinese Physics, 2006,55(08):3956-3963. [10]LIU Cong-xin.A new hyperchaotic dynamical system[J].Chinese Physics B, 2007, 16(11):3279-3285.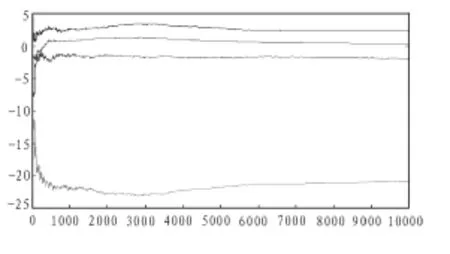

3 结束语

