非线性滤波算法性能对比
刘德春,谭 信
(1.阿坝师范高等专科学校 电子信息工程系,四川 郫县 611741;2.电子科技大学电子 工程学院,四川 成都 611731)
现在多传感器联合目标跟踪已经十分广泛,由于被动传感器不发射信号,只是被动的接受信号,因此只能测量目标的角度信息,而不能测量距离,因此状态方程和测量方程都是非线性的,因此非线性滤波算法得到了越来越广泛的研究和应用[1]。
本文中重要讨论三种非线性滤波算法,一类是扩展卡尔曼滤波,这种算法是利用泰勒级数展开方法将非线性问题转化为一个线性滤波问题,再用卡尔曼滤波方法进行求解,这种算法简单方便,但是在强非线性和非高斯条件下滤波性能急剧变差,甚至出现滤波发散;另一类是不敏卡尔曼滤波[2-3],这种算法是基于UT变换的,不需要对非线性系统进行线性化,而是利用采样点对状态向量的概率密度函数进行近似,近似后的概率密度函数仍然是高斯的;第三类粒子滤波算法[4,5]是近年来兴起的非线性滤波算法,是基于蒙特卡洛仿真的最优回归贝叶斯滤波方法,由于是利用随机样本对状态估计,因此该方法不受线性化误差和高斯噪声的限制,这是优于前两种滤波算法之处。
1 三种滤波算法简介
非线性系统的状态方程和观测方程如式1和式2所示。

其中,xk是目标的状态向量,zk是目标的观测向量,fk是系统的状态转移矩阵,hk是系统的观测矩阵,uk和vk分别是系统状态噪声和观测噪声,之间互不相关,协方差矩阵分别是Q和R。
1.1 扩展卡尔曼滤波算法
扩展卡尔曼滤波算法是一种常用的非线性滤波方法,由于状态噪声协方差矩阵和观测噪声协方差矩阵一直保持不变,因此其滤波结果好坏与过程噪声和量测噪声的初始估计有很大的关系,另外该算法只有当模型线性化误差较小时才有较好的滤波精度;相关参考文献指出泰勒级数保留的阶数越高,滤波的性能越好,但是计算量将大幅增大,实验证明,二阶扩展卡尔曼滤波器的性能要优于一阶,但是计算量要大很多,因此一般情况下只采用一阶扩展卡尔曼滤波算法。
扩展卡尔曼滤波递推步骤如下[1]:步骤1:状态的一步预测为

步骤2:协方差的一步预测

步骤3:量测值预测值
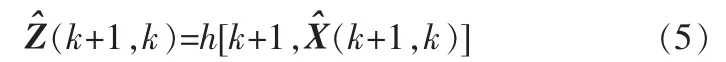
步骤4:量测预测值协方差

步骤5:滤波增益

步骤6:状态更新方程

步骤7:协方差更新
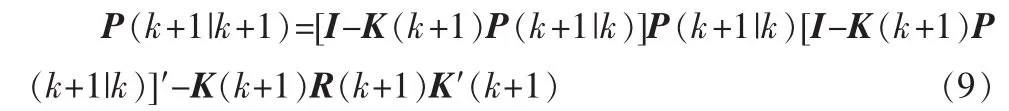
1.2 不敏卡尔曼滤波算法
当系统的非线性特性比较繁杂时,扩展卡尔曼滤波算法效果常常不能令人满意,为了得到更好的滤波效果,Julier等人便提出了基于UT变换的不敏卡尔曼滤波算法(UKF)。该算法利用一组近似高斯分布的样本点经过UT变换传递后,得到对状态分布函数的近似,该算法避免了EKF算法对非线性函数近似时引入的误差,得到了更好的滤波效果。
首先介绍UT变换的基本思想:
1)首先计算(2nx+1)个δ采样点ξi和其对应的权值Wi

式中,κ是尺度参数,满足κ+nx≠0。nx是状态向量的维数。
2)χi通过非线性传递得到新的样本点

3)y的估计均值与协方差估计如下:

不敏卡尔曼滤波的算法流程如下[6]:
3)进行观测值的更新


由UKF算法的流程可知,该算法不需要计算非线性函数的雅克比矩阵,从而大大节省了计算量,因此速度比EKF算法要快,并且UT变换能够更准确的估计非线性函数的均值和方差,因此滤波精度要比EKF算法要高。通过非线性函数传递时,对于任意非线性函数,UKF是后验均值和协方差都可以精确到二阶的高斯滤波,EKF只能获得一阶的精度,这就使UKF可以使用于任何动态模型。另外UKF算法对状态向量近似化后的概率密度函数仍然服从高斯分布的,因此对非高斯系统的滤波将会带来极大的误差。
1.3 粒子滤波算法
粒子滤波的基本思想是将所关心的状态矢量表示为一组带有相关权值的随机样本,并基于这些样本和权值计算出状态估计值。当随机得到的采样点足够多时,粒子估计得到的概率密度函数趋近于真实的概率密度,粒子滤波趋于最优贝叶斯滤波。
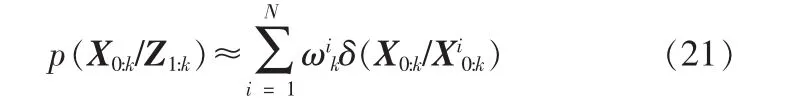

如果所选择的重要性密度概率密度条件独立,即
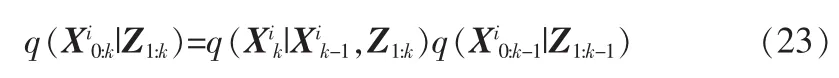
另外希望重要性概率密度函数只与前一个时刻有关,及满足马尔科夫过程,则

通过以上几式可得权值有如下关系:

当粒子数N→∞时,求出的后验概率密度函数接近于真实的概率密度函数。
粒子滤波在实际操作中存在粒子退化现象,即随着采样数的增加,许多粒子的权值会变得很小,样本的方差会随着时间增大。避免粒子退化现象可以采用两种方法:重采样技术和选取好的重要性密度函数。重采样技术可能会使样本枯竭,从而损失了粒子的多样性,样本枯竭问题还有待深入研究。选取好的重要性密度函数遵循两大原则:使重要性密度函数容易采样和使权系数的方差最小。
2 仿真实验与分析
2.1 仿真基本思想
仿真中系统采用非线性的模型[7],系统状态方程和量测方程如式26和式27所示。
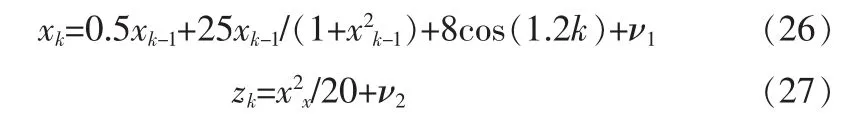
式中,状态噪声 ν1是服从伽马分布 G(3,2),量测噪声 ν2是服从高斯分布N(0,1),并且相互独立,仿真时长取为50 s。进行100此独立的蒙特卡洛仿真,粒子滤波粒子数取为200。
仿真结果如下:
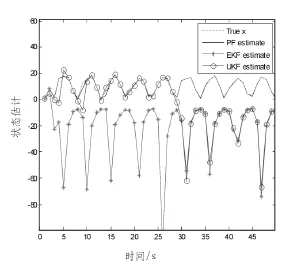
图1 滤波航迹与真实航迹Fig.1 Filtering track and real track

图2 三种滤波算法方差对比Fig.2 Comparison of variance of three filtering algorithm
三种滤波算法综合比较如表1所示。

表1 非线性模型下三种算法比较Tab.1 Comparison of three algorithms in the nonlinear model
通过以上仿真结果可以看出,由于采用了强非线性模型并且状态噪声是非高斯的,EKF算法的一阶泰勒级数展开的舍入误差较大,产生了明显的滤波发散,UKF算法也产生了较大的滤波偏差,而PF算法则要优于EKF和UKF算法。由表1可以看出,由于采用了非线性模型和非高斯误差EKF和UKF算法的方差急剧增大产生了发散,滤波性能急剧下降,PF算法的方差相对较小,滤波性能仍然较为良好,但是付出的代价是耗用了更长的仿真时间。
3 结束语
本文对三种非线性滤波算法进行了仿真,从计算速度角度来说,EKF和UKF要明显优于PF算法;从滤波精度角度来说,如果采用强非线性模型和非高斯噪声,EKF和UKF算法产生了明显的发散,而PF滤波算法性能依然良好。因此,在选择滤波算法时,在一般的非线性高斯环境中宜采用EKF算法,当非线性增大时可以采用UKF算法,当系统处于更复杂的非高斯环境时,最好采用滤波效果更好的PF算法。并且随着计算机能力的大幅提高,PF将具有更广泛的应用前景。
[1]何友,修建绢等.雷达数据处理及应用[M].二版.北京:电子工业出版社,2009.
[2]潘泉,杨峰.一类非线性滤波器-UKF综述[J].控制与决策,2005,20(5):481-488.PAN Quan,YANG Feng.Survey of a kind of nonlinear filters—UKF[J].Control and Decision, 2005, 20(5):481-488.
[3]江宝安.基于UKF滤波的单目标跟踪算法研究[D].合肥:国防科学技术大学,2003.
[4]胡士强,敬忠良.粒子滤波算法综述 [J].控制与决策,2005,20(4):361-365.HU Shi-qiang,JING Zhong-liang.Overview of particle filter algorithm[J].Control and Decision, 2005, 20(4):361-365.
[5]朱志宇.粒子滤波算法及其应用[M].北京:科学出版社,2010.
[6]吴凡.基于非线性滤波的机动目标跟踪算法研究 [D].西安:西安电子科技大学,2010.
[7]Merve R,Doucet A.The unscented particle filter[J].Technical Reprot CUED/FINFENG/TR 380, 2000:1-45.

