湖泊-河网耦合水动力水质模型研究

赵琰鑫，张万顺，汤 怡，吴 静

（武汉大学 资源与环境科学学院，湖北 武汉 430079）

1 研究背景

河网水动力水质模型是描述河道水体中污染物迁移转化规律的数学模型，是进行河流水质模拟和水污染控制的有力工具。近几年，河网水质模型得到长足的发展，如国外应用较多的美国的QUAL-2E，WASP模型等［1］。国内的彭虹等［2］建立了河流综合水质模型，李锦秀等［3］建立了三峡水库整体一维水质模型，储君达［4］、韩龙喜等［5］建立了河网水质模型并对模型求解方法进行了改进。但是以上研究仍存在一些不足，如其模型仅仅用于树状河网和单一河道，对于环状的河网有限制。其次，其模型考虑的水质变量及各个变量间的迁移转化不够全面。另外，针对复杂湖泊-河网区河道纵横、水系呈网状的特点建立的数值模型尚未见报道。

本文采用有限控制体积法对求解一、二维水动力学和水质模型控制方程，在一维、二维模型连接断面处，采用一维模型模拟河道水位、流量变化，并作为隐式变量带入二维湖泊模型进行求解，实现了一、二维模型的耦合，并根据太湖典型流域河网区实测水文和水质资料对耦合模型进行率定和验证。

2 湖泊-河网区的一/二维水动力水质耦合模型

2.1 一维河网水动力水质模型

连续性方程：

动量方程：

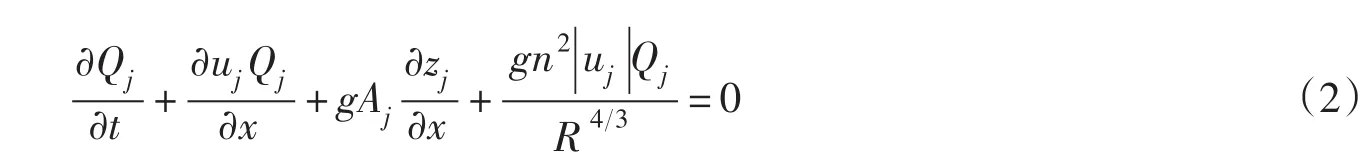
式中：uj为河网河道j的断面平均流速；Qj为河网河道j的流量；Aj为河道j的过水面积；t为时间；qj为河段j的侧流汇流流量；g为重力加速度；zj为河网河道j的水位；n为河道糙率；R为水力半径。

污染物迁移转换方程：

式中：Ci为污染物浓度；hj为河网河道j的水位；uj为河网河道j的流速；E为扩散系数；Sm为污染物排放量；kd为污染物的降解系数，kd=k0θT-20，T为水温，θ为系数，取1～1.08，k0为常温下的降解系数。

河网节点方程：

式中：cs是节点j的水质浓度；ciin为入流的水质浓度；Qiin为入流流量。

2.2 二维湖泊水动力水质模型

连续方程：

X方向动量方程：

Y方向动量方程：

式中：u、v为x、y方向的垂向平均速度；z为水面高程；h为水深；f为科氏力系数f=2Ωsinθ，Ω为地球旋转的角频率，θ为当地的纬度；γi为紊动黏性系数；ρa和ρw分别是空气和水密度；fw为风应力系数；wx、wy分别为x、y方向的风速。

水质迁移控制方程充分考虑水体污染物的对流、扩散降解作用。水质迁移控制方程：

式中：Ci为水中污染物i的浓度；Kx、Ky为x、y方向上的扩散系数。

2.3 一维、二维模型耦合方法 在一、二维模型连接断面处，根据两种模型模拟的水位、流量、浓度相等的条件，实现一、二维模型的耦合［6］。研究中通过设置过渡单元实现这一耦合，过渡单元为一维模型单元与二维模型单元的连接单元。图1为一维模型单元和二维模型单元的过渡单元网格布置。通过在连接断面处补充物理量之间的关系（水位、流量、浓度相等），实现了一维模型与二维模型的耦合，即：水位连接条件：Z1=Z2；流量连接条件：Q1=∫Uεhεdε；水质连接条件：C1=C2。其中：Z1、Z2分别为一、二维模型在连接断面处的水位；C1、C2分别为一、二维模型在连接断面处的水质浓度；Q1为一维模型在连接断面上的流量；Uε为二维模型在连接断面法向上的流速；h为水深；ε为一、二维模型连接断面坐标。

2.4 数值离散格式 将水动力和水质模型方程改写成统一形式

采用非正交非交错网格，在控制体内，对流项采用迎风格式处理，对上式进行积分和离散，得到对流扩散方程的离散方程：

其中：ap、anb分别是系数。

采用SIMPLE正交算法，获得自由表面η校正方程和速度修正方程，即

η校正方程：

速度修正方程：

表面和速度方程组属于同一类对角型的代数方程组，可以应用SIMPLE方法进行快速求解。

3 耦合模型的应用实例

3.1 区域概况 太湖流域位于长江三角洲，地跨江苏、浙江和上海二省一市，流域面积36500km2。流域内是我国经济最发达、目前经济发展最快的地区之一，水质污染问题十分突出。流域内河网纵横交错，闸站众多，水流运动十分复杂。

针对太湖流域复杂的河流水系网络结构特征，选取太湖湖西滆湖典型区域为研究范围，区域内骨干河道及次级河道总长度1642km，承担着防洪排涝、农田灌溉、城乡供水保障和交通航运等重要功能。区域内主要河道有：武宜运河、武进港、采菱港、太滆运河、扁担河、湟里河、芜申运河、孟津河、中干河等。其中，扁担河、南运河、采菱港、武进港等运河南部的水网承接运河来水，输向滆湖或太湖，区内河流主流向自西往东，自北往南。受长江、太湖相对水位的影响和通江河口闸门控制，河道流向不稳，常有滞流、倒流现象；整体河道呈现平原河网低流速、小流量的特性。

3.2 河网概化 太湖地区典型流域模拟计算中的河网、湖泊是在天然河网湖泊的基础上根据河道输水能力相等的原理进行合并、概化，概化河道的断面为梯形。依据河网结构和河道汇流特点，将河网划分成110个河段，共91个计算节点和519个计算断面。

3.3 模型参数

（1）糙率。参考相关研究报告，太湖河网区河道糙率取0.02-0.03，湖底糙率取0.002～0.025。

（2）降解系数。根据太湖流域河网区水质计算的经验值氨氮降解系数取0.05～0.20d-1，COD降解系数取 0.08～0.25d-1， TN降解系数取0.06～0.15 d-1，TP降解系数取0.05～0.08 d-1，。

3.4 模型的率定验证 采用2007年上游入流断面夏溪河夏溪桥站、湟里河湟里站、北干河东安桥站、江南运河常州站等水文站点流量过程，下游太湖百渎口站、大浦口站和宜兴站的水位过程，作为水动力计算的上下游边界条件，采用研究区域2007年排污负荷作为水质模型验证的计算条件，对模型进行率定验证，采用水文站实测水温作为水质模型计算的温度条件。

3.4.1 水动力模型的验证 采用太滆运河黄埝桥站和漕桥河漕桥站2007年逐日实测流量、水位过程对模型进行水动力学验证。水位验证结果如图2和图3所示，由图可知，水位计算值与实测值拟合程度较高，两验证断面绝对误差均小于0.55m，相对误差均小于12.97%，模型对河网水位模拟具有较高精度。

流量验证结果如图4和图5所示，由图可知，流量计算值整体变化规律与实测值变化规律具有较好的一致性。由于研究区域为平原河网区域，河道具有低流量、小流速的特点，部分时段河道流量及小，导致验证的相对误差较大。模拟值与实测值相对误差在20%以内的天数占全年的82.5%，模型精度较高。

二维湖泊水动力模型采用滆湖坊前站2007年逐日实测水位数据进行验证，验证结果见图6，由图可以看出，计算值与实测值规律呈现较好一致性，模拟的绝对误差控制在0.33m以内，相对误差控制在7.36%以内，模拟效果较好。

3.4.2 水质模型验证 在研究区域常规水质监测断面中选取与河网计算断面重合的黄埝桥、雪埝桥和漕桥等3个断面，采用2007年逐月实测水质数据对一维河网水质模型进行验证，模型计算结果与实测值对比，由表1黄埝桥、雪埝桥及漕桥断面氨氮、COD、TN和TP的模拟值和实测值的平均误差对比可以看出其相对误差多在30%以内，平均误差在25%左右，表明模型模拟值与实测值吻合较好，能够满足河网一维水质模拟的要求。

表1 各断面指标平均误差值（%）

表2 各指标相对误差值（%）

选取滆湖内的滆湖北常规水质监测点，采用2007年1月、4月、7月和10月实测水质数据对二维湖泊水质模型进行验证，由表2滆湖北氨氮、COD、TN和TP的模拟值和实测值的对比可以看出，其相对误差多在30%以内，平均误差在24%左右，表明模型模拟值与实测值吻合较好，能够满足湖泊二维水质模拟的要求。

4 结论

本文提出了适用于复杂湖泊-河网区域的一维、二维水动力和水质耦合数学模型。采用有限控制体积法对求解一、二维水动力学和水质模型控制方程，在一维、二维模型连接断面处，利用两种模型模拟的水位、流量相同的条件，将一维与二维模型有机连接为一个整体，实现一维模型与二维模型的耦合。应用太湖典型流域河网区实测水文和水质资料对耦合模型进行率定和验证，表明模型计算值与实测资料吻合较好，因此一、二维耦合模型的设计是合理的，适用于复杂湖泊-河网区的水动力和水质变化的模拟和研究。模型可用于深入分析滆湖与周边河网中水质浓度整体分布状况、响应关系，对流域不同污染物消减和水利调度调度处理等方案等进行情景模拟，并为太湖河网区的水污染治理工程提供技术支撑。

［1］郑孝宇，褚君达，朱维斌.河网非稳态水环境容量研究［J］.水科学进展，1997，8（1）：25-31.

［2］彭虹，张万顺，夏军.河流综合水质生态数值模型［J］.武汉大学学报，2002，35（4）：56-59.

［3］李锦秀，廖文根，黄真理.三峡水库整体一维水质数学模拟研究［J］.水利学报，2002（12）：7-10.

［4］褚君达.河网对流输移问题的求解及应用［J］.水利学报，1992（7）：30-34.

［5］韩龙喜，金忠青.三角联解法水力水质模型的糙率反演及面污染源计算［J］.水利学报，1998（7）：30-34.

［6］Wanshun Zhang，Yan Wang，Hong Peng.A coupled water quantity-quality model for water allocation analysis［J］.Water Resource Manage，2010（24）：485-511.