基于根轨迹控制的球杆系统
王晓勤,韩亚军
(重庆科创职业学院机电技术中心,重庆 永川 402160)
随着科学技术的发展,控制对象日益复杂,对控制精度和控制性能的要求也日益提高,传统控制方法已经难以满足这些要求,因此需要提出更为先进的控制方法[1-2].但是在实际系统的研究中,存在着许多难以克服的困难,因此有必要首先在实验室进行基础性的研究,而球杆系统正是一个理想的实验模型.球杆系统是一个典型的多输入多输出耦合系统,具备了一个非稳定性系统所有的动态特征[3],通过对球杆系统控制方法的研究,可以验证自动控制原理中的许多控制方法和控制理论,对于摸索复杂系统的控制方法,解决控制过程中系统的鲁棒性、稳定性问题都有着重要的意义.
1 球杆系统模型
V型槽轨道、不锈钢球、连杆、直流伺服电机(DC servo motor)及大小齿轮箱减速机构组成球杆系统.V型槽轨道由两部分组成,其一侧为不锈钢杆,另一侧为直线位移电阻器.球杆系统装置如图1所示.
当球在轨道上滚动时,通过测量不锈钢杆上输出电压可测得球在轨道上的位置.导轨的一端固定,而另一端则由直流伺服电机的经过齿轮减速,再通过固定在大齿轮上的连杆带动进行上下往复运动.导轨与水平线的夹角可通过电位计或电机编码器的转动角度和简单的几何计算获得.这样,通过设计一个反馈控制系统调节直流电机的转动,就可以控制小球在轨道上的位置[4].
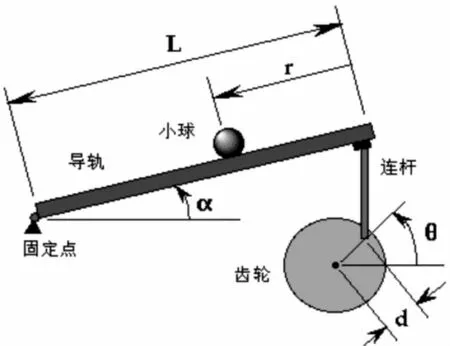
图1 球杆系统示意图
球杆系统是输入量为电机转角θ、输出量为小球位置r的系统.输入量θ利用直流伺服电机自带角度编码器来测量,输出量r由轨道上电位器的电压信号来获得.系统组成框图如图2所示.

图2 球杆系统框图
2 球杆系统建模
球杆系统是一个非线性不稳定系统,为了便于分析,将球杆系统模型分解成球杆机械部分模型(联系小球的位置r(t)和导轨的仰角α(t))、角度模型(联系导轨的仰角α(t)和电机的转动角度θ(t))和电机模型(联系输入电压u(t)和电机的转动角度 θ(t))[5].
2.1 球杆系统机械模型
根据牛顿定理可知,小球在导轨上滚动的动力学方程为
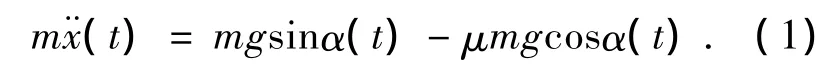
小球在导轨上滚动时,摩擦力很小,可以忽略不计,则方程式(1)可近似为

假设导轨和水平面之间的夹角α(t)非常小,将(2)式线性化得到

将上式进行拉普拉斯变换得到以下传递函数:

2.2 球杆系统角度模型
在实际控制中,导轨和水平面之间的夹角α(t)由直流电机的转角输出来实现.导轨与水平面之间的夹角α(t)与电机转角θ(t)是非线性的静态关系,可近似得到

2.3 球杆系统的电机模型
球杆系统中的电机响应速度很快且电机转角θ(t)对电压u(t)的响应时间常数也很小,故可将电机数学模型近似为一个纯增益K[6].
则整个球杆系统等效传递函数框图,如图3所示.

图3 球杆系统等效传递函数框图
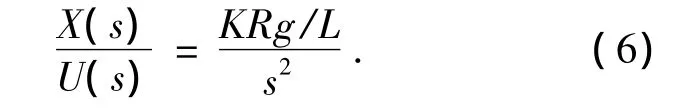
为简化模型,可将KRg/L的值近似为1.由图3可知,整个球杆系统的传递函数为
3 根轨迹控制
根轨迹的主要思想就是通过分析系统的开环零极点位置,来分析闭环系统的特性,通过增加极点或零点的方法(校正器),根轨迹以及闭环系统的响应都发生改变.
球杆系统的传递函数为
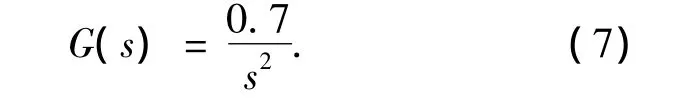
为了便于讨论和仿真,要求系统调整时间ts≤1 s,最大超调量Mp≤10%.
首先确定闭环期望极点sd的位置,由最大超调量:

可以得到ζ≈0.6.设θ为位于第二象限的极点和0点的连线与实轴方向的夹角.由ζ=cos(θ)可以得到θ=0.938306.
又由

可以得到ωn=6.76641.于是可以得到期望的闭环极点为6.76641(-cosθ± jsinθ).
未校正系统的根轨迹在实轴和虚轴上,不通过闭环期望极点,因此需要对系统进行超前校正,设控制器为

其次,计算超前校正装置应提供的相角,已知期望的闭环主导极点和原来的极点的相角和为

因此校正装置应提供的相角为

再次,设计超前校正装置,已知θ=0.938306,对于最大值α值和γ角度可由下式计算得到

所以有 γ =0.469135.
按照最佳确定法作图规则,在球杆系统根轨迹计算图中画出相应的直线,如图4所示.

图4 球杆系统根轨迹计算图
求出超前校正装置的零点和极点,分别为

校正后系统的开环传递函数为

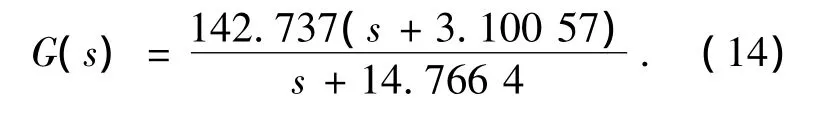
4 实验结论及分析
实时控制实验采用了深圳固高公司的实验平台,在Simulink环境下运行,结果如图5~7所示.

图5 没有校正的球杆系统根轨迹图

图6 有校正的球杆系统根轨迹图

图7 带校正的球杆系统阶跃响应
自动控制工程中的根轨迹法,经过融入球杆系统稳定性的重要因素后,在进行系统分析和设计中,使用根轨迹设计器使得分析和设计系统更加方便,能够更加直观地反映出校正前后的各项动态性能指标.
[1]刘艳军,范路平.机床控制器中命令解释程序的设计与实现[J].重庆文理学院学报:自然科学版,2009,28(5):68-70.
[2]韩亚军,黄贻培,梁雪峰.基于查询表的一维比例积分模糊控制器的实现[J].重庆文理学院学报:自然科学版,2009,28(3):59-61.
[3]Salvatore S,Esposito E,Miller J.Ball& beam control system[J].IEEE Transactions on Automatic Control,2002,30(3):376-388.
[4]Qiu L,Zhou K M.Feedback control[M].Prentice Hall,2005.
[5]胖永新,金迪,孟宪东.球杆系统的建模、仿真与控制器设计[J].武汉大学学报:工学版,2005,33(5):550-553.
[6]孙大卫,张国良,陈励华.基于根轨迹的直流伺服电动机PID控制器参数确定法[J].实验技术与管理,2009,26(4):38-41.

