基于朴素贝叶斯的EM缺失数据填充算法
邹 薇,王会进
(暨南大学 信息科学技术学院,广东 广州510632)
在数据泛滥的今天,迫切地需要一种将数据转换成有用的信息和知识的数据挖掘技术。然而,由于信息无法获取或者在操作过程中被遗漏等原因,现实中的数据往往存在大量的缺失[1]。数据缺失对数据挖掘的过程和结果有严重的影响:首先,系统丢失了大量有用的信息;其次,系统中所表现出的不确定性更加显著,系统中蕴涵的确定性成分更难把握[2];第三,包含空值的数据会使挖掘过程陷入混乱,导致不可靠的输出;第四,可能直接影响到数据挖掘模式发现的准确性和运行性能,甚至导致错误的挖掘模型[3]。因此,在数据预处理过程中,缺失数据的处理是一个重要的环节。
目前,国外对数据缺失问题的研究取得了很多成果,提出了最近似值替换方法、随机回归填补法、神经网络、贝叶斯网络等理论来解决缺失数据填充问题。国内对填充缺失数据的研究还处在一个开始的阶段,只有银行、保险业等在针对其自身具体的应用进行了缺失数据处理的研究。
总体上说,对缺失值的处理分为三大类:删除元组、数据填充和不处理[4]。其中,处理数据缺失最简单的方法是删除元组,当缺少类标号时通常这样做(假定挖掘任务设计分类),但是当每个属性缺少值的百分比变化很大时,该方法性能特别差[5]。处理数据缺失的有效方法是使用最可能的值填充缺失值,可以用回归、贝叶斯形式化的基于推理的工具或决策树归纳确定[6]。近年来,学术界提出了很多数据填充算法。宫义山提出了基于贝叶斯网络的缺失数据处理方法[7],彭红毅针对数据之间存在相关性且为非高斯分布这种情况提出了ICA-MDH数据估计方法[8],Hruschkaetal.使用贝叶斯算法对实例中的缺失值进行估计[9]。
在众多算法中,EM算法能通过稳定、上升的步骤可靠地找到全局最优值,算法适应性更强。尽管Gibbs抽样(Gibbs samplig)[10]、GEM(Generalized EM)算法、Monte Carlo EM算法都改进了EM算法,但EM算法收敛速度慢的缺点仍然没有得到很好的解决。基于此,本文提出结合朴素贝叶斯分类改进传统EM算法的方法填充缺失数据的新算法。给EM初始值界定了范围,提高了EM算法的收敛速度和算法的稳定性,克服了边缘值造成EM算法结果偏差大的缺点,实现了良好的缺失数据填充效果。
1 朴素贝叶斯分类的EM数据填充算法及其改进
1.1 符号定义
首先对算法中使用到的符号进行定义,如表1。

表1 符号定义一览表
1.2 传统EM算法介绍
EM(期望最大化)算法是一种流行的迭代求精算法,它的每一步迭代都由一个期望步(expectation step)和一个最大化步(maximization step)组成。其基本思想是,首先估计出缺失数据初值,计算出模型参数的值,然后再不断迭代执行E步和M步,对估计出的缺失数据值进行更新,直到收敛。EM算法的具体描述如下:
(1)随机选择K个对象代表簇的中心,以此猜测其他的参数;
(2)反复执行E步和M步对参数进行求精,直到收敛。
①E(期望)步:用概率 P(Xi∈Ck)将每个对象 X指派到簇 Ck。

其中,P(Xi|Ck)表示簇 Ck中 Xi的概率,是对象 Xi的簇隶属概率。
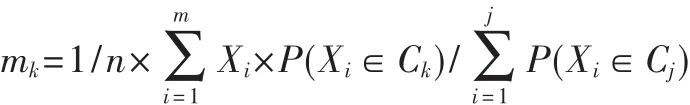
1.3 EM算法改进
EM算法随机选择对象作为簇的中心,会导致EM算法聚类结果的不稳定性,以及边缘数据对整个算法影响过大,使得填充数据正确率偏低。本文提出了基于朴素贝叶斯的EM缺失数据填充算法。本算法使用朴素贝叶斯算法对源数据进行分类,将分类结果作为EM算法使用范围,在每个类中反复执行E步M步直至收敛,充分利用了EM算法容易达到局部最优的优点,使得EM算法更好地聚类,更快地收敛,从而得到更准确的数据填充值。本文算法的具体描述如下:
(1)利用朴素贝叶斯算法对源数据进行分类;
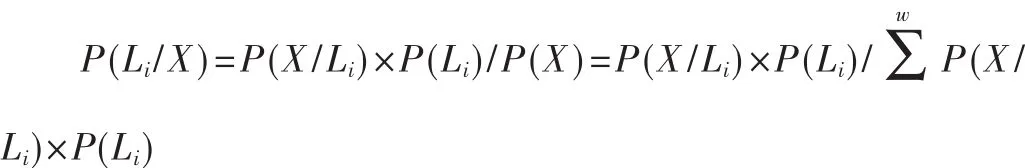
其中,P(Li)为先验概率,等于 SCi/Sd。
P(X/Li)为Li条件下X的条件概率密度函数。假定X/Li为一整体T,该概率密度函数母体ξ是离散型,则L(θ∧;T1,T2,…,Tn)=L(θ;T1,T2,…,Tn),满足这个式子的 θ∧(T1,T2,…,Tn)就有可能产生 T1,T2,…,Tn的参数 θ的值,其 相 应 的 统 计量 θ∧(ξ1,ξ2,…,ξn)称 作 θ的 极 大似然估计量。如果该概率密度函数母体ξ是连续型,则只需求出使得 L(θ∧;T1,T2,…,Tn)=∏f(Ti;θ)达到极大的θ∧(T1,T2,…,Tn),便可得到极大似然估计,即InL(θ∧;T1,T2,…,Tn)=L(θ;T1,T2,…,Tn)。
计算出P(Li/X),分类法将预测X属于具有最高后验概率(条件X下)的类。即朴素贝叶斯分类预测X属于类 Ci,当且仅当 P(Ci/X)>P(Cj/X)1≤j 这样就得出了每个数据元组X所属的类,分类完成。 (2)利用(1)分类的结果分别作为新的数据集,在这些数据集中分别使用EM算法计算期望最大化值。 在类 L1,L2,…,Lw这 W 个分类中,分别选出 K个对象代表簇的均值,再反复执行E步和M步对参数进行求精,直到收敛。 E(期望)步:用概率 P(XLi∈CLiK)分别将类 Li中的每个对象XLi指派到簇CLiK中。 算法收敛后,用计算得到的最大化值mLik作为类Li中簇k的最大化值,并使用这个值填充缺失数字。 上节描述的算法由程序实现,具体的算法伪代码如下: (2)将朴素贝叶斯算法的分类结果分别作为EM的初始范围。分别在每个类中使用EM算法,计算出期望最大值。 从UCI机器学习数据库中,选取4个没有数据缺失的完整数据集,表2列出了它们的详细信息。 表2 论文中使用的数据集 实验设计具体步骤如下: (1)将原始数据集准备二份,一份作为原始集,一份作为测试集。用MCAR(missing completely at random,完全随机缺失)方法随机去掉测试集的不同比率的属性值,并剔除原有类标; (2)使用本文算法对(1)后的测试集的属性值和类标进行预测,填充缺失值和类标志; (3)反复进行试验20次; (4)本文使用填充数据与真实数据的平均绝对离差(MAD)和标准平均离差(RMSD)作为比较标准。其中MAD=|Y填充值i-Y真实数据|/20×n,RMSD=(Y填充值i-Y真实数据)2/n]1/2/20。 其中 Y填充值i表示第 i次填充的数据,Y真实数据是真值,n 表示缺失个数。 对于不同缺失率的数据集,分别使用EM算法和本文算法进行填充,比较结果如表3~表5所示。 表3 缺失率15%下MAD、RMSD比较结果 表4 缺失率30%下MAD、RMSD比较结果 表5 缺失率50%下MAD、RMSD比较结果 由上述三表可以看出,在缺失率不同的情况下与经典EM算法相比,本文算法稳定,且减少了与真实数值的偏差,这样使得实际运用中的填充数据值更真实地反映数据信息。EM算法提出较早,GEM算法、Monte Carlo EM算法和界定折叠法等都改进了EM算法,相比较于这些算法,本文充分利用了EM算法容易实现局部最优的特点,将EM初始范围界定在一个类内,使得EM算法很好地聚类和收敛,使得填充值更接近于真实数值。 数据缺失是数据预处理中亟须解决的问题,本文为填充缺失数据提出了基于朴素贝叶斯的EM数据填充算法。该算法使用朴素贝叶斯分类算法的结果作为EM算法的初始范围,然后按E步M步反复求精,利用得到的最大化值填充缺失数据。该算法充分利用了EM算法容易实现局部最优的特点,使得EM算法更好地聚类,更快地收敛,从而得到更准确的数据填充值。实验结果表明,该算法得到了预期的效果。由于本论文主要是针对数值型属性进行分析,下一步的研究是考虑非数值型属性缺失问题。 [1]GRZYMALA-BUSSE J W.Rough set approach to incomplete data.In∶LNAI 3070,2004∶50~55. [2](加)Han Jiawei,KAMBER M.数据挖掘概念与设计[M].北京:机械工业出版社,2008. [3]LAKSHMINARAYAN K,(1999).Imputation of missing data in industrial databases[J],Applied Intelligence 11:259-275. [4]HUANG X L.A pseudo-nearest-neighbor approach for missing data recovery on Gaussian random data sets[J].Pattern Recognition Letters,2002(23):1613-1622. [5]GRZYMALA-BUSSE J W,FU M,(2000).A comparison of several approaches to missing attribute values in data min-ing[C].In∶Proc of the 2nd Int’Conf on Rough Sets and Current Trends in Computing.Berlin∶Springer-Verlag,2000:378-385. [6]ZHANG S C,QIN Y S,ZHU X F,et al.Optimized parameters for missing data imputation.PRICAI06,2006∶1010-1016. [7]宫义山,董晨.基于贝叶斯网络的缺失数据处理[J].沈阳工业大学学报,2010,32(1):79-83. [8]彭红毅,朱思铭,蒋春福.数据挖掘中基于 ICA的缺失数据值的估计[J].计算机科学,2005,32(12):203-205. [9]HRUSCHKA E R,EBECKEN N F F.Missing values prediction with K2[J].Intelligent Data Analysis,2002,6(6)∶557-566. [10]GEMAN S,GEMAN D.Stochastic relaxation,Gibbs distribution and the Bayesian restoration of images[J].IEEE Trans onPattern Analysis and Machine Intelligence,1984(6)∶721.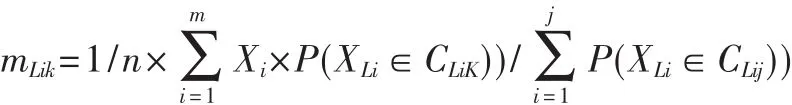
1.4 算法伪代码实现



2 实验结果及分析