OFDM符号定时同步算法的研究

王晓斌 孙 强

OFDM(orthogonal frequency division multiplexing)正交频分复用技术，是一种特殊的多载波传输技术，发送端将数据调制到多个相互正交的子载波上同时发送。其优点频谱利用率高、传输速率大、抗多径衰落能力强。在宽带无线通信系统中，WiFi、WiMax及4G得到了广泛的应用，因此国内外围绕OFDM系统的实现和标准协议的制定展开全面的研究。但OFDM技术对时间和频率的偏移比较敏感，时间偏移会导致符号间干扰 (ISI)，频率偏移会破坏子载波之间的正交性，引起载波间干扰 (ICI)，均使系统性能急剧下降。要想实现OFDM系统的良好性能，需要精确时间与频率同步，所以同步成为OFDM技术中的一个研究热点。

1 SC定时同步算法

Schmidl＆Cox定时同步算法是利用2个码元长度的训练序列做自相关，由自相关值来进行符号定时和频偏联合估计，其数据格式如图1所示。

图1 Schmidl＆Cox算法的数据时域结构

CP1表示训练序列1的循环前缀，CP2表示数据符号的循环前缀，其中训练序列1用来做符号定时同步和小数频偏估计，训练序列2用来估计整数频偏。仅在偶数频率的子载波上发送PN序列，奇数频率发送全零PN序列，经过IFFT后，在时域上就得到前后2部分对应相等的样值，并以这些作为第1训练序列的值。算法的基本思路:定时估计的目的就是为了寻找训练序列1的起始位置，首先在接收端通过接受信号在N个样值长度的窗口内做自相关，这里N为子载波个数，如:

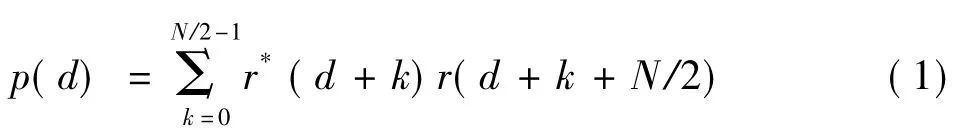
相关函数p(d)的值是计算前半序列和后半序列的相关值，d为抽样点的位置。由式 (1)和图1中训练序列1的时域结构可知，当d为训练序列1的起始位置时，p(d)的值出现最大值，接收机以这个值为符号定时同步的检测点。为了对p(d)做能量归一化处理，引入R(d)值，它计算的是前半序列的能量，如

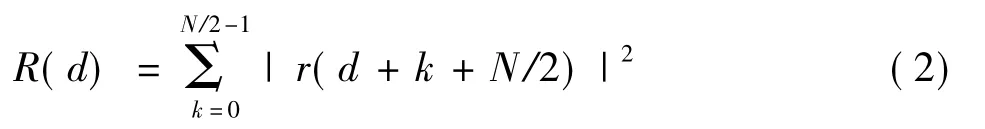
对p(d)做能量归一化处理，如

从图2的仿真结果中可以看出，Msc(d)曲线会出现平台区。在0点附近，估计函数有一段“平顶”，这样会给同步带来误差，算法本身的抗噪声能力不强，特别是在恶劣的无线传输环境下，不利于通信系统的实现。

图2 Schmidl＆Cox定时偏移估计函数曲线

2 改进的算法

针对Schmidl＆Cox符号同步算法的缺点，对此算法进行改进，分为2部分。

1．引入新的训练序列，其具有良好的自相关性质，可提高OFDM的同步性能。

2．引入自相关序列及自相关函数。从上面的仿真可知曲线存在平台区，为了对由CP引起的平台进行过滤，根据频域前导字序列良好的相关特性，引入新的自相关序列及自相关函数，构造一种倒序的训练序列，其序列符号P具有以下形式:P=［AB］，其中B为A的倒序。

设计的思路:随机产生序列pn(n)，用QPSK调制方式调制pn(n)序列得到复数信号a(k)=［1+j，1 －j， －1+j，1 － j…．］，在偶数子载波上插入M复数序列，奇数子载波插0，经过IFFT后得到前N/2个样值与后N/2样值对应相同的训练序列train(k);而A=［train(0)train(1)…train(N/2－1)］，所以P=［train(0)train(1)…train(N/2－1)train(N/2－1)…train(1)train(0)］。

频域前导字序列ak具有很好的自相关性，由于p(n)是其线性变换，因此也具有很好的相关特性:

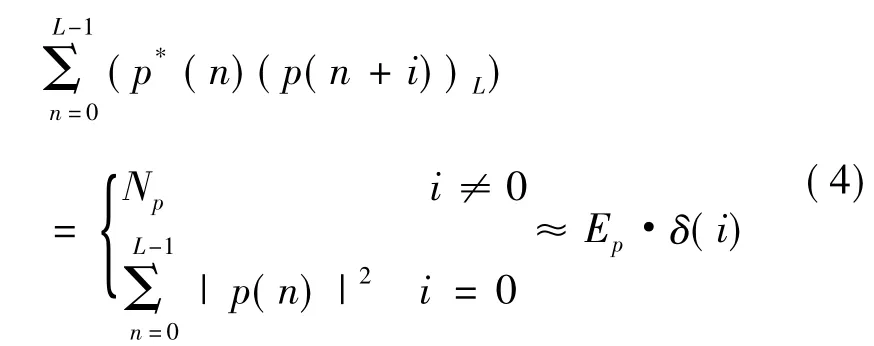
L=N/2为其周期长度，Ep表示前导字p(n)，0≤n≤L－1一个周期的总能量，δ(i)表示脉冲函数，Np表示相关噪声。从第二部分对Schmidl＆Cox算法的仿真结果可知，由于CP1的影响，定时估计曲线出现一个平台区，定时估计需要检测平台开始下降的位置;而在实际存在噪声和多径的影响后，这个下降的拐点很难准确检测到。

由前导相关性分析可知，利用式 (4)消除由CP引起的平台，从中选择出没有循环移位的前导字的位置。对此引入新的自相关序列 (d表示相关窗口的起始位置):

将 (5)代入 (4)，化简有:

其中，W(d)表示此时总的零均值噪声，从(6)式可知，只有当相关窗的起始位置恰好在前导字的开始时，p1(d)才可以达到最大值。在－Ncp≤d－^d≤0区间内p1(d)不会达到最大值，因此由Schmidl＆Cox算法引起的相关值平台区变成了一个指示前导字起始位置的尖峰。对p1(d)做归一化可得相关窗的能量:

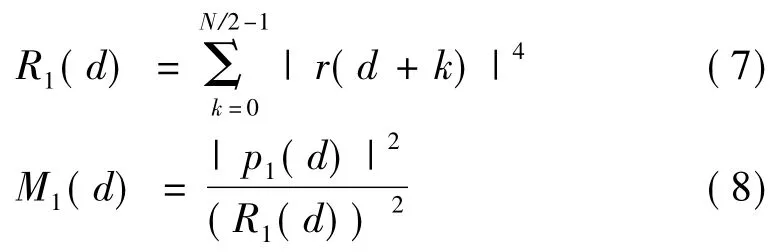
由 (8)式得知，本文所提的符号定时估计为:

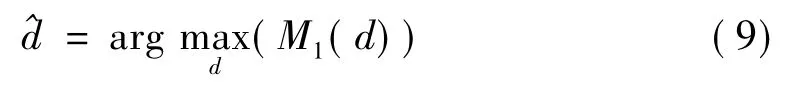
3 建模与仿真结果分析

基于前面描述的定时同步算法，在Matlab环境下进行系统建模与仿真，图3是接收机定时同步流程图。

图3 接收机定时同步流程图

首先对本文所提出的同步算法进行计算机仿真验证。仿真过程中，系统的主要参数选为:子载波个数为N=512;循环前缀CP=64;采用AWGN信道模型。

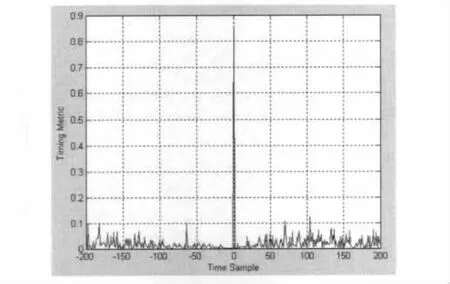
图4 改进算法的定时偏移估计函数曲线

从图4的仿真结果可以看出，改进算法的定时估计函数曲线只有惟一的峰值，并且峰值是在正确的定时估计位置。因此改进的定时同步算法有效地消除了循环前缀造成的平台效应，使得定时估计的精度明显地提高，进而提高OFDM通信系统的整体性能。

为了能从估计函数得出定时估计位置，SC定时算法一般采用均值法，就是找到最大值点和2个最大值的90%的点，分别位于最大值的左右边，定时估计被认为是这2个点的均值，即^d=d1+d2，其中Msc(d1)=Msc(d2)=0.9×maxMsc(d);而改进算法中直接检测式 (9)中的值，找出M1(d)最大值对应的^d，^d即为定时估计的位置。

仿真使用的帧结构如图5所示;为了仿真效果，在CP前面添加N点随机数据，因此准确的定时位置应该定在第1个CP的末端，N=512，CP=64，即为512+64+1=577。

图5 仿真的帧结构

多径衰落信道的条件:各径时延PathDelays_vector=［0 5 10 12 25］，各径相对功率PathGains_vector= ［0 －10 －15 －20 －22］ (db)，随着不同的信噪比，对改进算法和SC算法进行定时估计位置的统计如表1所示。

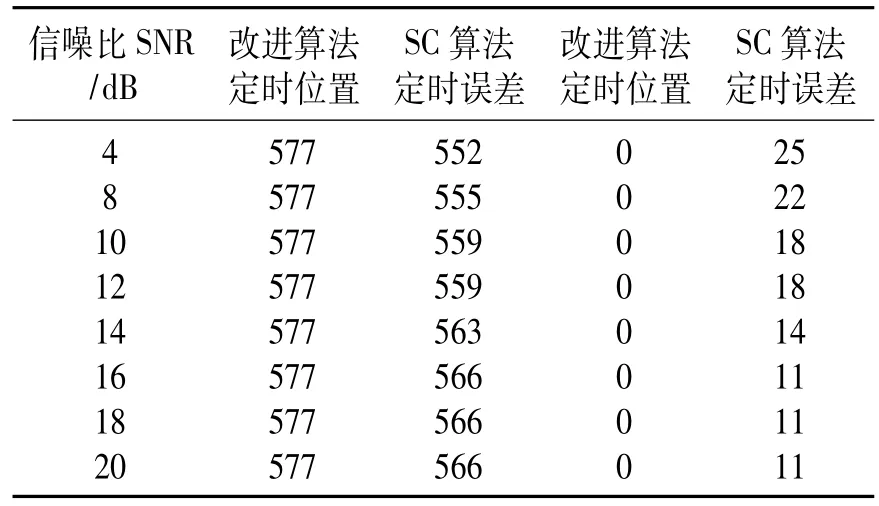
表1 2种算法的定时估计位置及误差

从表1的仿真结果得知，SC算法的定时估计位置基本处于循环前缀的中心附近，存在很大的定时误差，对接收机的解调性能造成严重的影响。而改进算法能够估计出准确的定时位置，进而对提高OFDM系统的整体性能打下良好的基础。所以定时同步算法在多径衰落信道环境下能够提供准确的定时点，有利于改善通信系统的可靠性，适于要求可靠性高的无线通信系统，如WLAN，LTE等。

4 结论

针对OFDM接收机的符号定时算法进行研究和计算机仿真，在对Schmidl＆Cox算法的缺点分析后，提出利用新的训练序列及改进的相关序列实现定时的准确度，改变由Schmidl＆Cox算法带来的相关最大值的平台，减少了接收机检测定时点的难度，使系统的同步性能有明显地提高。

［1］ 佟学俭．OFDM移动通信技术原理与应用［M］．北京:人民邮电出版社，2003．

［2］ Sehmidl TM，Cox D C．Robust frequency and timing synchronization for OFDM［J］．IEEE Tram．Commun．，1997，45:1613－1621．

［3］ Ch N Kishore，V U Reddy．A technique for dominant path delay estimation in an OFDM system and its application to frame synchronization in OFDM mode of WMAN［M］．EURASIP Journal on Wireless Communications and Networking，2006，2006(2):18 －25．

［4］ 黄慧.一种OFDM定时同步与载波频偏估计算法［J］．电路与系统学报，2008，4．

［5］ Tian Ye，Tan Zhenhui，Zhu Gang．An improved joint timing and frequency fast synchronization method for OFDM［J］．Journal of the China Railway Society，2007，29(4):52-56．

［6］ Zhou Yiqing，Hu Aiqun．A new synchronization algorithm for OFDM systems using training frame［J］．Journal of China Institute of Communications，2001，22(4):12-18．

(责任编辑:诸 红)