基于博弈方法的产品组合资源配置决策研究

王运志，胡耀光，张瑞君

（1. 北京理工大学 机械与车辆工程学院，北京 100081；2. 中国人民大学 商学院，北京100872）

基于博弈方法的产品组合资源配置决策研究

王运志1，胡耀光1，张瑞君2

（1. 北京理工大学 机械与车辆工程学院，北京 100081；2. 中国人民大学 商学院，北京100872）

0 引言

在制造业全球化、集群化和信息化的发展趋势下，制造企业信息化应用已从运营支持层转而向管理和决策层的方向发展，我国制造业在全球市场竞争中也面临着在快速变化的商务环境中合理配置企业资源、实现价值增值的敏捷反应与科学决策的需求。当前制造企业经常需要面临的制造决策问题是在产品制造过程中，通常需要在有限的资金、设备等资源条件下，使获得的资源能够得到最大限度利用以满足制造要求，实现最优的生产状态。

产品组合生产中的制造资源优化配置问题即是当企业在在不确定的技术、原材料和市场需求约束下进行多种产品制造时，需要选择最优的产品生产组合，使每一产品的生产都能达到最理想的资源配置。在传统最优化理论、遗传算法等研究中通常以企业整体收益、运营指标、设备利用率、市场需求满意度等作为优化的目标。但在现代制造企业中，产品不仅需要满足企业短期盈利的目标，在企业决策者对某种产品没有偏好的情况下，决策应保证各产品在资源竞争中都能够获得最优的资源配置和最大的收益，从企业的战略决策角度更能满足企业长期发展的需要。近来有很多研究采用新的方法来更好地解决产品组合资源配置决策问题，例如进化方法[1]和约束理论方法[2]等。本文采用完全信息下的静态博弈的方法，建立多维决策模型，将产品作为资源竞争的主体，以每一产品都选择最优的资源配置，最大化本产品的收益为目标，选择在给定的约束条件下资源分配的均衡解，达到每一产品的最优生产状态。

1 产品生产函数及变量

任何产品的生产行为都是在特定的生产条件（如技术、资源等）下进行的，这种特定的生产技术关系决定了一个生产过程的投入和产出的数量上的对应关系，描述这种对应关系的工具就是生产函数[3]。

生产函数是一种经验研究方法，是以数据为样本，通过数学方法的拟合、检验和修正得到的。在决策研究中，可以采用生产函数作为决策效用函数，以益损值为横坐标，以效用值为纵坐标来表示两者关系。同时，决策的预见性要求效用曲线能够反映决策者的偏好和对风险态度，因此需要根据决策者对相同的益损问题（获取收益或避免损失）的反应对生产函数进行修正，把决策战略者对风险态度的变化在此坐标系中描点而拟合成一条曲线。效用曲线有保守型、激进型、中间型和混合型等类型，可以采用指数拟合、Cobb-Douglas生产函数或前沿生产函数等。

在组合产品生产函数的构建过程中，首先要识别决策问题中的变量和这些变量与目标函数之间的定量关系。通常情况下，制造过程变量包括：资源变量、技术参数和决策要素等；变量关系主要分析决策变量与生产绩效变量的可控制变量之间的关系。例如，Norden提出一套制造决策定量化分析的方法，将决策分析过程分为4类基本事件：计数、分类、连接和比较，然后通过测量、连接、比较、建模的过程建立一个可以描述问题的目标、约束和其他关系的模型[4]。

利用企业已有的制造信息化系统，如ERP系统等，可以表述产品的费用-收益函数如下：

其中：物料成本：ΣC*Cq (C 为物料的标准价，Cq为该物料的定额用量)

资源消耗费用：ΣRr*Rq（Rr为资源标准费率，Rq为资源标准用量）

资源管理费用（制造费用）：ROr （Ror为资源管理费用）

物料的管理费用：MOr (MOr 为采购件的管理费用)

外协费用：ΣRPr

对拟合后的产品收入（效用）和产品成本（资源投入）关系曲线，在预测的最大销售量 和最小可行产量的决策空间范围内，选择合理区间离散处理后，作为一个有限博弈的策略空间和支付。

2 多维博弈决策模型

博弈论研究存在外部经济条件下的个人选择问题，在应用博弈论方法进行混合产品选择问题的研究中，产品本身作为资源竞争的决策主体，参与人主动选择行动（或战略）以最大化产品的效用，即产品的收益水平。博弈论的基本概念包括参与人、行动、信息、战略、支付（效用）、结果和均衡。

假设博弈G有N个博弈方，第n个博弈方的可行战略集为Kn(n =1,2,...,N)。记博弈方n 的战略为kn∈Kn，则博弈G的支付向量u=(u1,u2,...,uN)T可以定义为笛卡儿乘积空间K=K1×K2×...×KN到N维实数空间RN上的映射，即u:K→RN，从而博弈方n 在战略组合为k =(k1,k2,...,kn-1,kn,kn+1,...,kN) 时的支付为：

式中：[ . ]n表示支付向量的第n个分量。

在传统（classic）的博弈描述方式中，博弈的战略式表述在参与人较多时难以表示，而扩展式表述不适合用于计算。从表示形式上，博弈G的的支付向量u即为一个N维实数集合，因此可以采用多维数据库来表示一个博弈结构。

在博弈的多维结构描述中，参与人、战略和支付是描述一个博弈所需要的必须要素，因此一个博弈多维模型的基本维度可定义为：

其中：

1）N个参与人的策略空间维度：每个参与人作为一个维度，维度成员为该参与人的策略空间；

2）参与人维度：博弈的参与人集合作为一个维度，维度成员为每个参与人；

3）支付维度：表示参与人的效用水平，维度成员可以对应决策者在不同的偏好和对风险态度下的效用表示；

4）结果维度：博弈模型的求解结果，维度成员可以是不同种类型的博弈结果。

另外，在该模型上扩展其他博弈要素可以解决类型，例如增加行动要素维度，可以通过决策中的行动顺序来解决动态决策问题；增加信息集要素维度，可以支持不完全信息决策问题的描述。

在应用多维博弈模型解决混合产品资源配置问题时，将每一竞争资源的产品作为博弈参与人，可选的资源投入作为每一产品的战略空间，产品效用函数作为支付维度。在多维数据库系统，例如ESSBASE中建立博弈模型后，可利用多维数据库的数据挖掘、搜索等技术对模型进行求解。

3 博弈决策模型的求解

应用博弈论进行决策的核心问题是求解博弈模型，即寻找博弈的均衡。本文在基于多维数据模型描述的博弈决策问题基础上，提出均衡结果的求解方法。

博弈的纯策略纳什均衡解，可以根据Nash均衡的存在性定理Ⅱ判定解的存在性：

在n人战略式博弈中，如果每个参与人的纯战略空间Si是欧氏空间上一个非空的、闭的、有界的凸集，支付函数ui(s)是连续的且对si是拟凹的，那么这一对策中存在纯策略纳什均衡。

但是Debreu 等给出的纯策略纳什均衡存在性定理是在十分严格的条件下的充分性定理，对于制造资源的配置决策问题，参与人的支付函数可能是有限策略组合的离散点集，而且不是连续且拟凹的。唐小我等给出有限战略博弈纯战略纳什均衡解的搜索算法[5]：

定义函数fn为博弈方n采用战略kn时的支付最大化判别函数，即给定其他博弈方的战略k-1= (k1,k2,...,kn-1,kn+1,...,kN)，如果kn∈arg max{Un}，则 fn=1 ,否则 fn=0。

战略组合k=(k1,k2,...,kN)∈K是纯战略纳什均衡的充分必要条件为F(k)=N，因此F(k)= N可以用来判断一个博弈的纯战略纳什均衡。如果知道博弈的支付组合，则可以通过博弈方支付最大化函数对可能成为纳什均衡的战略组合作标记，然后，检查支付组合的标记次数是否等于参与博弈的博弈方的个数来判断相应的战略组合是否是一个纳什均衡。

在基于ESSBASE构造的多维数据库模型中，使用该方法求解纯战略纳什均衡的算法脚本可以表示为：

最后，通过对每一战略组合在参与人维度上判断所有参与人的标记次数F(k)=N，即可判定战略组合是否为纯战略纳什均衡。

4 算法描述及示例

假定某企业生产A、B、C3种产品，虽然产品的生产规模和收益不同，但每一种产品对企业都非常重要。企业决策者选择将一部分资金分配到3中产品中，使每一种产品都尽可能得到达到最大收益所需的资金，并使企业有尽可能高的投资收益。

首先，分析企业现有制造信息系统中的制造数据，得到该三种产品在过去8个月中的生产成本与收益如表1所示。

表1 过去8个月中的产品的费用-收益 (单位：百万元)

并考虑未来市场需求和企业规模等因素，预计未来的资金投入量范围如表2所示。

表2 计划投入资金 (单位：百万元)

然后，对每一产品的生产函数采用多项式拟合后，并考虑决策者的风险偏好等因素，修正后的产品效用曲线如图1所示。

图1 产品效用曲线

根据上述产品收益-成本关系曲线，在预测的每一产品最大和最小资源投入范围内，选择以1 个单位（百万元）为区间做离散处理后，3个产品的资源配置战略集合和支付如表3所示。

表3 产品战略和支付(单位：百万元)

建立多维博弈模型，并求解模型的均衡解。分析当企业最大投入资金分别为380和350时，博弈模型的均衡解及整体投资收益比率如表4所示。

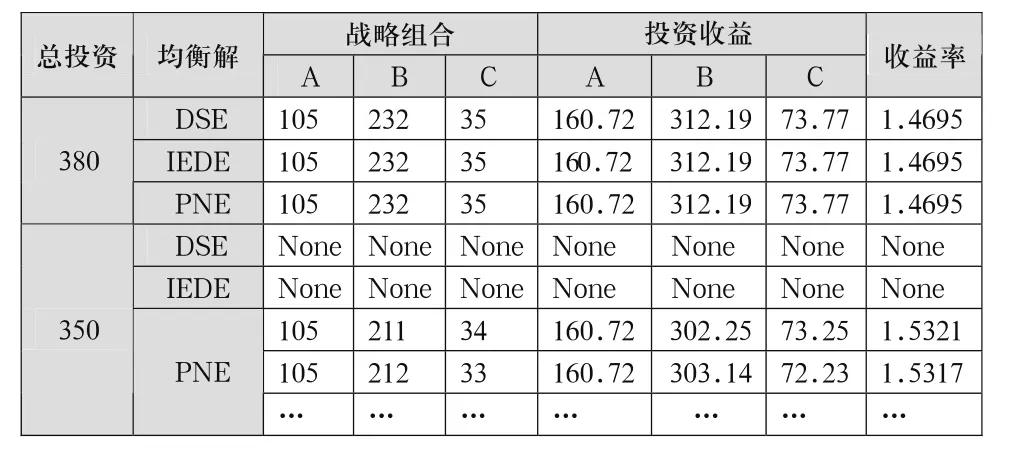
表4 多维博弈模型的均衡解 (单位：百万元)

根据以上计算结果，当企业最大投资为380时，三种均衡解都是战略组合(105, 232, 35)，是最优资源配置决策；当企业最大投资为350时，不存在占优战略均衡和重复剔除的占优战略，存在多个纯策略纳什均衡，结合将整体投资收益比率作为资源配置效率指标，战略组合(105,211,34)是最优资源配置决策。

5 结论

本文研究了使用非合作博弈理论进行产品组合资源配置决策研究的方法，将制造资源效用和战略组合进行定量化描述，作为博弈分析的要素来构建多维博弈模型。相比于其他以资源配置整体收益为优化目标的算法，本文采用求解博弈模型的均衡解作为决策结果，避免了忽视单一产品收益的缺陷。应用示例说明了本算法的实用性。由于纯战略纳什均衡解的不唯一性，本研究方法还需要进一步研究战略的混合纳什均衡解和非确定环境下的决策问题求解。

[1]Ioannis G.Tsoulos,Pandian Vasant,“Product mix selection using an evolutionary technique,”Power Control and Optimization,2009:240-247..

[2]RAINER SOUREN, HEINZ AHN and CHRISTIAN SCHMITZ,“Optimal product mix decisions based on the Theory of Constraints”,International Journal of Production Research,2005,43(2):361-374..

[3]孙巍.生产资源配置效率-生产前沿面理论及其应用[M].社会科学文献出版社,北京:2000:83-93.

[4]Norden, P.V.,“Quantitative techniques in strategic alignment,”IBM Systems Journal,1993,32:180-197.

[5]唐小我,倪得兵.有限战略式博弈纯战略均衡求解的新算法[J].管理工程学报,2006,20(2):137-140.

A game theoretic approach to product-mix resource allocation

WANG Yun-zhi1, HU Yao-guang1, ZHANG Rui-jun2

本文针对有限资源下的产品组合资源配置决策问题，提出了基于博弈理论的解决方法。应用定量化分析方法来表示制造资源效用和配置战略，将产品作为资源竞争的主体，使用定量化的决策要素作为维度来构造一个多维博弈模型，求解博弈模型得到资源配置决策的最优解。

产品组合资源配置；多维博弈模型；定量化决策

王运志（1974 -），男，辽宁大连人，博士，研究方向为制造资源配置、商务智能。

TP274

A

1009-0134(2011)4(上)-0072-04

10.3969/j.issn.1009-0134.2011.4(上).23

2010-10-29

国防科技基础研究基金项目（C172009C001）