基于模拟法下EENS值的系统可靠性裕度分析
蒋群,任惠,陈远
(华北电力大学电力工程系,河北保定071001)
在最初20世纪30年代的时候,电力系统由于统计数据不完整,加上没有有效的评估技术,人们对可靠性的认识不足等原因,可靠性评估发展比较缓慢。随着电力系统向高压、远距离、大容量方向发展,系统规模变大,安全性问题更加显著,对电网的安全可靠运行有了更高的要求[1-3]。之后的世界范围大的电力系统停电事故,造成了巨大的损失,引起人们对可靠性的重视,也带来了可靠性研究工作的发展[4]。
发输电系统可靠性评估的基本目的是在考虑发、输电设备的随机故障特性情况下,对发电系统是否拥有足够的发电容量,主输电网是否拥有充足的输电容量,其是否能为负荷点提供合乎质量要求的供电能力进行综合性定量概率评价[5]。
对发输电系统进行有预见的可靠性评估可以发现系统薄弱环节,为设备的运行、维护、维修提供指导意见,还能为电力公司的决策提供参考信息,所以发输电系统的可靠性评估引起各国学者的关注和研究[6]。在传统的可靠性评估中主要采用的是N-1准则。N-1准则是指正常运行方式下,电力系统中任意一元件(如线路、发电机、变压器等)无故障或因故障断开后,电力系统应能保持稳定运行和正常供电,其他元件不过负荷,电压和频率均在允许范围内[7-10]。N-1准则用于单一元件无故障断开条件下电力系统静态安全分析,或单一元件故障断开后的电力系统稳定性分析,即动态安全分析[11]。
随着地方电厂接入的增多,电网的暂态稳定运行水平受到一定的影响,正常方式或检修方式导致机组失稳的情况普遍存在,如根据N-1准则进行稳定预控,必将牺牲一定的可靠性及保护的配合性[12]。传统的确定性的潮流计算方法往往不能全面地反映系统的运行状态,且分析结果一般比较保守。随着电力系统的发展,引入了基于风险评估的方法。由于该方法能够反映评估对象的概率因素和后果因素,因此正逐渐应用于电力系统安全分析,并逐步取代传统的确定性方法[13]。在风险评估中主要采用的就是蒙特卡洛模拟法。
本文主要利用蒙特卡洛法建立系统参考序列。参考序列的建立是通过逐渐增加系统节点负荷来实现的,随着负荷的增加,系统可靠性裕度逐渐降低。然后设计新的系统状态同参考序列相比较,根据新状态在参考序列中的位置来确定可靠性裕度的大小。
1 蒙特卡洛模拟法原理
蒙特卡洛法是运用随机数序列产生一系列的实验样本。当样本数量足够大的时候,基于中心极限定理和大数定律,样本的均值可以作为数学期望的无偏估计[14]。
用U来表示系统的不可用率,xi表示系统状态

系统不可用率的估计值可由样本均值给出。

式中,N是系统状态样本数。
样本方差定义为
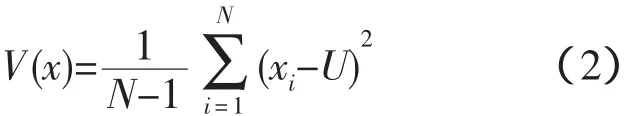
样本均值方差
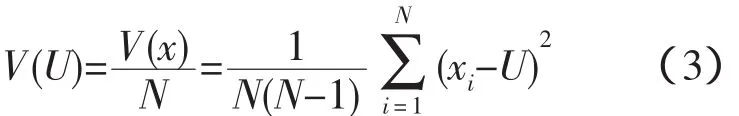
样本均值的标准差

蒙特卡洛模拟精度可用方差系数来衡量,定义为

方差系数可作为蒙特卡洛仿真中的收敛准则。
蒙特卡洛法有3种抽样方法:1)状态抽样法;2)元件状态持续时间抽样法;3)系统状态转移抽样法。
本文主要采用状态持续抽样法,假定元件的初始状态为正常状态,然后对每个元件当前的状态持续时间抽样。假定元件运行时间和故障状态下的修复时间服从指数分布,然后根据元件的故障率和修复率确定该元件在给定时间段内的状态和状态持续时间[15]。当给定时间段内所有元件的状态和持续时间确定后,就可以获得系统的状态序列和持续时间。

元件i状态持续时间的抽样值为

式中,Ui是[0,1]上均匀分布的随机数;如果当前元件为正常状态,λi为第i个元件的故障率;如果是故障状态,则λi表示修复率;Ti为该元件故障持续时间。本文的抽样中主要考虑的是发电机和线路的随机故障。
2 可靠性评估流程
文中主要是将电量不足期望值EENS作为可靠性指标,因为EENS是能量指标,对于进行可靠性经济评估、最优可靠性、系统规划等有重要的意义,因此选取它来作为评估指标。评估基本步骤如下。
1)建立负荷和元件模型;2)利用蒙特卡洛模拟选择系统状态,包括随机确定母线负荷和元件状态;3)对状态进行评估,并计算切负荷量及经济损失后果;4)统计可靠性指标。
蒙特卡洛模拟中EENS的计算公式
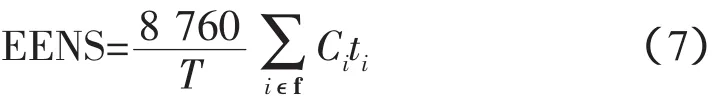
式中,ti为状态i的持续时间,h;Ci为状态i的切负荷量,MW。
可靠性评估流程图见图1。
在负荷削减中采用的是最优负荷削减模型[16],目标函数和约束条件如下
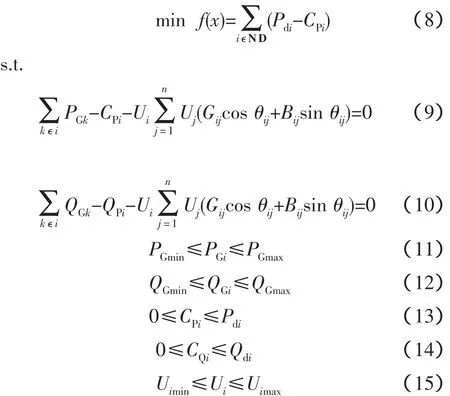

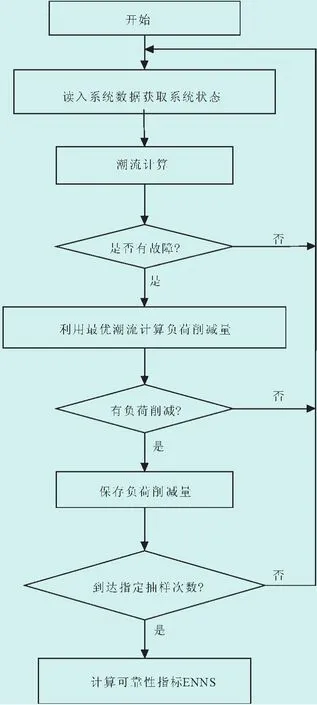
图1 可靠性评估流程图
其中,式(9)为有功等式约束;式(10)为无功等式约束;式(11)、(12)为发电机有功和无功出力约束;式(13)、(14)为负荷有功和无功约束;式(15)为节点电压约束;式(16)为输电容量约束。Pdi为节点i初始状态的有功功率;CPi为优化潮流计算后系统实际负荷;QGi、QGmin、QGmax为发电机的无功功率和上下限;Ui、Uimin、Uimax是节点电压幅值及其上下限。
3 算例分析
本文利用MATLAB7.1编写可靠性程序,采用上述的最优负荷削减模型对IEEE 24节点算例进行可靠性分析,利用蒙特卡洛状态持续时间抽样法对系统进行模拟,仿真计算中考虑发电机和输电线路的随机故障。负荷模型采用年峰负荷来计算指标,所以计算出的EENS是年度化指标。
在仿真中先算出基本状态下的EENS值,再逐步增加系统节点负荷,仿真模拟中共设计9个参考状态[17],然后计算每个参考状态下的EENS。随着负荷增长率的加大,系统的压力也越来越大,系统的可靠性裕度逐步降低。参考状态的EENS值见表1。
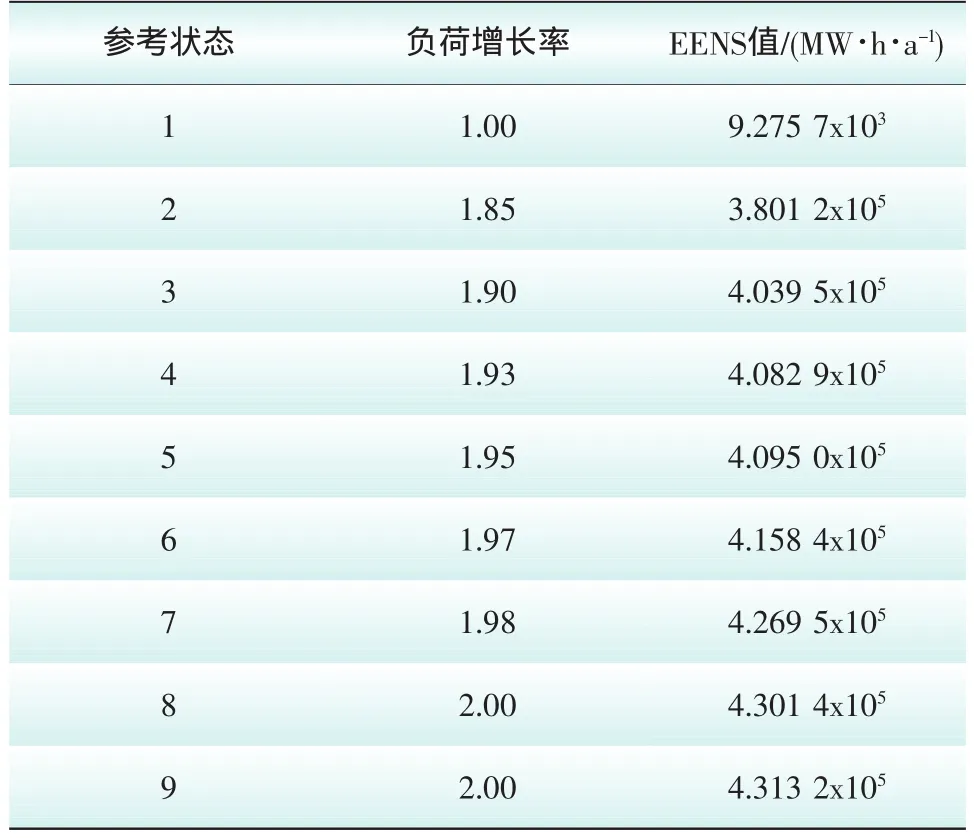
表1 参考状态的EENS值
设计x、y2个新的状态同参考序列比较,根据它们在参考序列的位置来判断状态的可靠性裕度,从上而下裕度依次是减小的。
x状态:负荷是基本状态下的1.5倍,线路2、3、19、20、32、33断开。
y状态:线路3、4、22、25、30、32、34、36、38断开,节点6的50 MW转移到节点8,另外50 MW转移到节点10;节点1的80 MW和节点3的90 MW分别转移到节点5(50 MW)、节点7(20 MW)节点15(100 MW),负荷为基本状态下的1.79倍。
通过仿真计算出2个状态下的EENS值,如表2所示。

表2 x和y状态下的EENS
将x、y2个状态下的EENS值同表1中的值对比,可以得到状态x在参考状态1~2,状态y接近参考状态2,从而可以说明状态y系统压力是高于状态x的压力,状态x的可靠性裕度大于状态y的裕度。
利用蒙特卡洛模拟法计算完x、y2个状态的EENS值后,在N-1准则下分别计算各个线路断开及负荷转移后系统的EENS值,然后加和即为系统总的期望缺供电量。
表3和表4是在N-1准则下仿真出的状态x和y下的EENS的值。
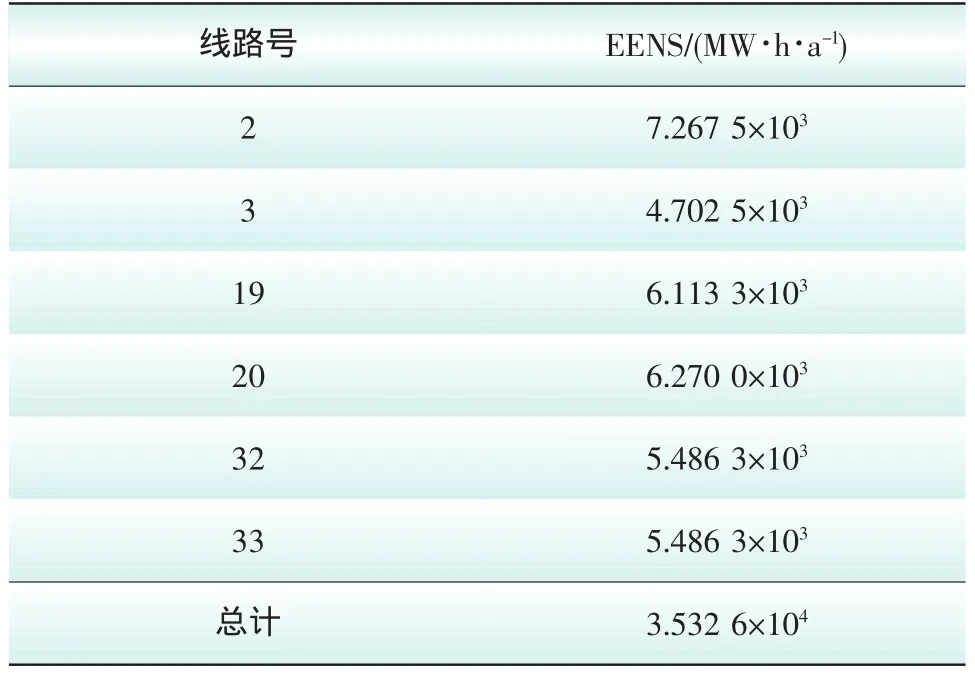
表3 N-1准则下状态x线路断开后EENS的值

表4 N-1准则下状态y线路断开后EENS的值
表5为在N-1准则下计算出的x状态出现电压越限的节点。

表5 N-1准则下x状态母线电压幅值
通过数据分析发现,在N-1准则下得到的状态x是不安全的,因为状态x下节点2、5、10出现电压越限的情况,这主要是由于一些临界的紧急事件导致的,并且该状态的EENS值要大于状态y下的值;计算中状态y并未出现电压越限,说明状态y比状态x更安全[18]。
结果显示,采用蒙特卡洛这种概率的方法计算出的结果同传统的方法是不同的。传统准则下认为状态y的可靠性是高于状态x的,但是蒙特卡洛模拟法得到的状态y的EENS值大于状态x、y的可靠性裕度小于状态x。说明状态y下可能在保护方面存在隐性故障,导致了系统压力水平的增高。所以利用该方法可以提供更多的信息,令操作人员更加全面地分析系统的压力水平,从而保证系统安全可靠的运行。
4 结论
本文提出一种概率的方法来衡量系统的安全性和压力水平,它对系统状态的描述更加可靠和全面。因为该方法不单单考虑最有可能发生的紧急事故,还考虑到了会导致更严重的多重故障的小概率事件,这些小概率事件有可能就是系统保护中的隐性故障。EENS作为计算指标,和停电的概率、范围、持续时间紧紧相关,利用它来反应系统可靠性比利用母线或者输电线的过负荷更准确全面。
由于确定性N-1安全评估方法的分析与结果以及需采取的调整措施都很明显直观,所以在今后的研究中,应将这种概率的方法同传统的方法结合起来,使得系统可靠性评估更加完善。
[1]郝宁,朱永利.基于改进重要抽样法的输电系统可靠性评估[J].陕西电力,2011,39(1):21-25.
[2]王磊,赵书强.基于云模型的输电系统可靠性评估[J].电网与清洁能源,2010,2(11):19-23.
[3]王磊,王秋莎.基于改进未确知有理数的输电系统可靠性评估[J].陕西电力,2010,38(7):20-24.
[4]马振宇.电网可靠性的蒙特卡洛仿真研究[J].电力系统保护与控制,2009,37(14),55-58.
[5]郭永基.电力系统可靠性分析[M].北京:清华大学出版社,2003.
[6]谢日文晔.电力系统及其发输电组合系统可靠性评估[J].四川电力技术,2005(5):51-53.
[7]刘理峰,李志买,郭肖辉,等.配电网N-1算法研究应用[J].陕西电力,2010,38(2):46-49.
[8]陈文婕,刘晋,周云海,等.考虑负荷转移限制的配电网可靠性评估[J].陕西电力,2010,38(11):23-27.
[9]张小娟,李泽荣,张重远,等.基于最小路法的配电网可靠性评估[J].电网与清洁能源,2010,26(8):24-28.
[10]杜鹃.基于最小值法的配电系统可靠性评估[J].陕西电力,2011,39(2):37-40.
[11]金玉琪,张浩,王函韵.基于“N-1”准则的安全稳定预控在电网运行中的运用[J].华东电力,2007,25(4):92-95.
[12]陆波,唐国庆.基于风险的安全评估方法在电力系统中的应用[J].电力系统自动化,2000,11(25):61-64.
[13]王英,谈定中,王小英,等.基于风险的暂态稳定性安全评估方法在电力系统中的应用[J].电网技术,2003,27(12):37-41.
[14]李文沅.电力系统风险评估—模型、方法和应用[M].北京:科学出版社,2006.
[15]宋云亭,郭永基,程林.大规模发输电系统充裕度评估的蒙特卡罗仿真[J].电网技术,2003,27(8):24-28.
[16]赵渊,周家启,刘洋.发输电组合系统可靠性评估中的最优负荷削减模型分析[J].电网技术,2004,28(10):34-37.
[17]KIRSCHEN D S,JAYAWEERA D,NEDIC D P,et al.A Probabilistic Indicator of System Stress[J].IEEE Transactions on Power Systems,2004,19(3):1650-1657.
[18]KIRSCHEN D S,JAYAWEERA D,NEDIC D P,et al.Probabilistic indicator of system stress[C]//Proc PMAPS 2002—7th Int Conf.Probabilistic Methods Applied to Power Systems,Naples,Italy,Sept.2002:65-71.

