计及灵敏度影响的水电站主接线可靠性分析

蔡政权，卫志农，孙国强，谢佳家，申张亮

（1.河海大学 能源与电气学院，江苏 南京 211100；2.瑞安电力有限责任公司，浙江 温州 325200；3.南京供电公司，江苏 南京 210008）

我国水力资源丰富，水电在我国能源结构中占有重要的地位，提高水电站的运行可靠性对电力系统的安全稳定运行有着至关重要的作用。水电站的可靠性是电能质量的一种重要指标，可靠发电不但使发电量增加，故障恢复费用下降，而且可靠的电能在当下的电力市场中也更具有竞争力。

目前电气主接线可靠性的评估方法包括表格法、停运表法、专家系统法、蒙特卡洛模拟法、马尔科夫状态空间法等。文献[1-2]应用了邻接终点矩阵求主接线图的最小路集和最小割集完成对主接线可靠性的评估；文献[3]应用区间不确定性的方法对主接线进行了分析；文献[4-5]运用n+2马尔科夫模型对主接线可靠性进行了分析。在以往文献中都未能将断路器的故障率修改模型与灵敏度的指标相结合。本文将断路器的故障率修改模型引入灵敏度分析，并运用邻接终点矩阵法与元件可靠性模型结合，考虑水能出力的影响，对各个元件参数进行灵敏度分析。通过分析，能够使断路器的投资和布点位置更加合理。

1 元件可靠性计算

可靠性指标的定义应考虑以下因素：

1）所定义的指标要能全面地反映系统的运行、控制特征；

2）便于不同方案或不同系统的比较；

3）对工程决策有指导意义。在参照了国内外可靠性指标研究的基础上。

本文选用了以下电站可靠性指标进行分析：电站出力受阻概率LOLP（loss of load probability）；电站出力受阻时间期望LOLE（loss of load expectation）；电站出力受阻频率FLOG（frequency of loss of load）；电站出力受阻平均持续时间DLOL（duration of loss of load）；电站出力受阻电力期望EDNS（expected demand not supplied）；电站出力受阻电量期望EENS（expected energy not supplied）。

1.1 元件可靠性计算公式

电气主接线状态的变化和事件的发生与其元件状态的变化是相关联的，在进行主接线可靠性研究中，需要考虑元件各种不同状态及其影响以及各元件的相关性，使得可靠性模型与系统实际条件相一致。

电气主接线形式和出线数目虽然不同，但是元件与线路之间都是串、并联关系。考虑到3个以上元件同时故障的可能性极小，可利用最小路、最小割集的思想，并且以元件的连通为判断标准，求得元件的一阶到三阶的最小割集，从而将元件之间的连接关系转化为求取可靠性逻辑的串并联关系。利用计算转移率的串并联公式，求得元件的转移率。在求取各等效元件模型之后，用来取代主接线图上的线路，即可建立可靠性评估模型。本文还将继电保护的拒动、活动性故障等因素并入元件的可靠性模型中。在分析过程中将常开开关作为对应的常闭开关的替换设备，相应的开关切换时间作为替代设备投运的时间。

电力系统可靠性统一的计算公式为[6]：

式中，x为系统状态，假设系统由m个元件构成，Si代表第i个元件的状态，则x=（S1，…，Si，…，Sm），由于Si是一个随机变量，因此x是一个随机矢量；X为系统状态空间，F（x）为以系统状态x为自变量的可靠性指标测试函数；P（x）为系统状态x的概率分布函数；E（F）为随机函数F（x）的概率期望值。在此设定元件有故障和正常两种状态，ui为元件i的无效度，ai为元件的有效度，则Si是一个离散的随机变量[5]。

设元件i的故障率为姿i，修复率为滋i，则有

由以上公式列出以下2种基本的可靠性指标计算公式，其他的公式也可以由此而推导。

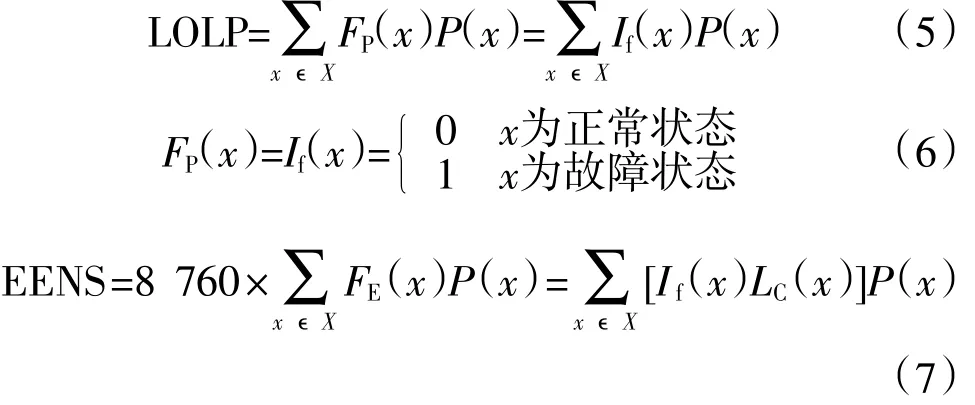
式中，LC（x）为在系统故障状态x下为使系统恢复到一个静态安全运行点所必需的最小负荷削减量[6]。

1.2 断路器故障率参数修改模型

断路器的故障包括接地故障、操作故障以及误动、拒动等故障形式。造成断路器故障的原因有：断路器的各个部件由于制造、安装等原因造成的本体故障；倒闸操作中的电流对断路器造成的磨损故障；切除故障时的故障电流对断路器的损坏造成的故障[3]。因此，实际系统中应根据断路器所处的位置、操作规律的区别，在统计平均故障率的基础上对断路器的故障率进行修正，使其更加符合工程实际，其具体修正公式如下：

1）线路断路器[7]

式中，K1为静态系数，一般取0.3；K2为切除短路系数，一般取0.4；Li为线路长度，km；Lp为平均长度，km；K3为操作系数，一般取0.3；ni为断路器每年的实际操作次数，np为年平均操作次数，我国取24次/a；姿p为断路器统计平均故障率。

2）主变压器—机组侧断路器[7]

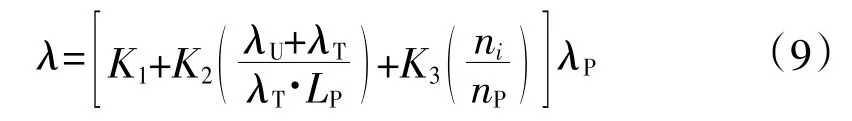
式中，K1、K2、K3、LP、nP与前同；姿U为水轮发电机组故障率；姿T为主变故障率；姿L为线路故障率；ni为机组每年操作次数。

2 灵敏度分析

电力系统可靠性的灵敏度分析实质是求取各可靠性指标对电力系统设备参数的偏微分，因此灵敏度指标反映了设备参数的微小变化所引起的系统可靠性的改变程度及改变趋势[6]。计及灵敏度影响的可靠性模型的基本思想是：通过灵敏度的计算，找出对可靠性影响比较大的元件集合，通过该集合中的元件，组合计算出电力系统的可靠性指标。电气元件的可靠性参数对系统总指标的贡献有大有小，而且可通过元件参数的灵敏度指标来反映其对系统可靠性指标贡献的大小[8]。

可靠性指标的灵敏度分析是求取期望值E（F）对系统元件可靠性参数的偏微分，可表示为：

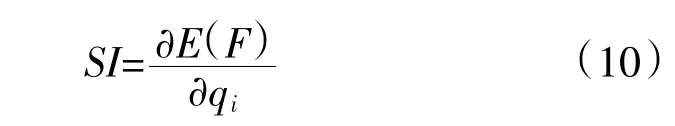
式中，SI为可靠性指标的灵敏度；qi为元件i的可靠性参数，包括故障率姿，修复率滋，容量C，计划检修率姿义。可靠性指标对元件i的故障率姿i的灵敏度为：

由式（10）可知，LOLP对元件i的故障率姿i的灵敏度为：

由于If（x）与姿i之间没有直接的函数关系所以

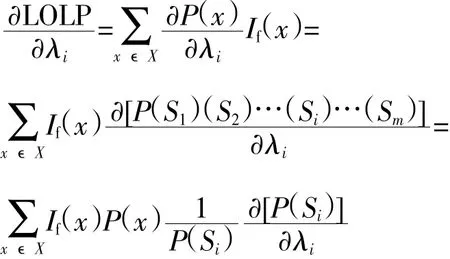
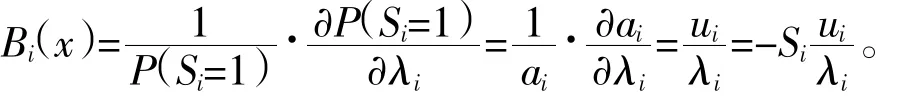
当Si= 0时，

因此LOLP、EENS对故障率的灵敏度为：

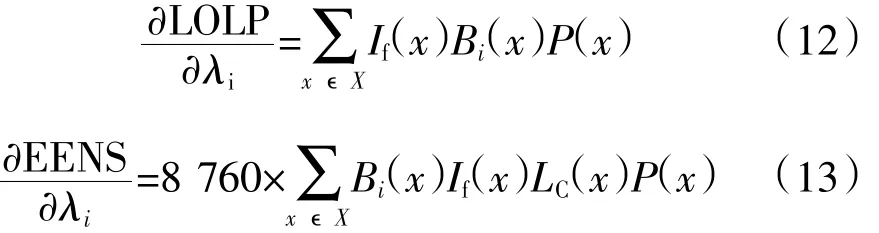
其他的可靠性指标对滋、C、姿义的灵敏度同样可以利用式（9）求得。

3 故障搜索算法

用网络连通性进行主接线可靠性评估的关键是求出线到电源点的通路，并进一步求得相应的故障割集事件。传统搜索最小路搜索算法的方法存在一些局限性：1）难以处理同时存在单向支路和双向支路的混合有向网络；2）难以处理母线这样的单节点元件（发电机、母线、负荷视为单节点元件）；3）一般只对单电源单负荷点的系统进行分析，推广到多电源多负荷点的系统比较困难。因此，本文应用矩阵技术对传统的搜索最小割集的方法进行了改进。通过定义特殊的矩阵乘法规则，用矩阵的乘法运算完成对最小割集的搜索过程。以下为邻接终点矩阵的运算规则：

设N=（V，E）是一个简单有向网络，其中E是弧集，V={v1，v2，…，vn}是节点集。

1）定义n阶方阵A1=[aij1]为网络N的邻接矩阵[9]

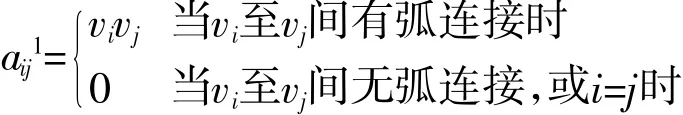
2）定义n阶方阵R=[rjk]为网络N的终点矩阵

显然，A1中包含了N中所有长度为1的路径，矩阵R反映了N中每条弧的终点。另外由矩阵A1和R之间的乘法运算产生新矩阵A2=[aij2]。A2的元素aij2由以下法则得到：

由此可以得到A2所有非零元素构成的所有长度为2的最小路。类似，可以得到A3，A4，…，An原1，从而得到网络的任意节点之间的所有长度的路径。将A1，A2，…，An原1中对应位置（i，j）的非零元素组合在一起，就得到从节点i到节点j间的所有最小路。

运用邻接终点矩阵法求取最小割集进行可靠性分析的流程如图1所示。

4 算例分析

本文针对沟滩皮水电站电气主接线进行了可靠性及其灵敏度分析。图2是构皮滩水电站电气主接线图。该主接线高压侧电压为500 kV，5台发电机，4回出线，发电机单机容量600 MW，每回出线700 MW，出线长度为180 km，年利用小时数为3222 h，月平均水能出力如表1所示，元件可靠性原始数据如表2所示[7]。

表1 月平均水能出力

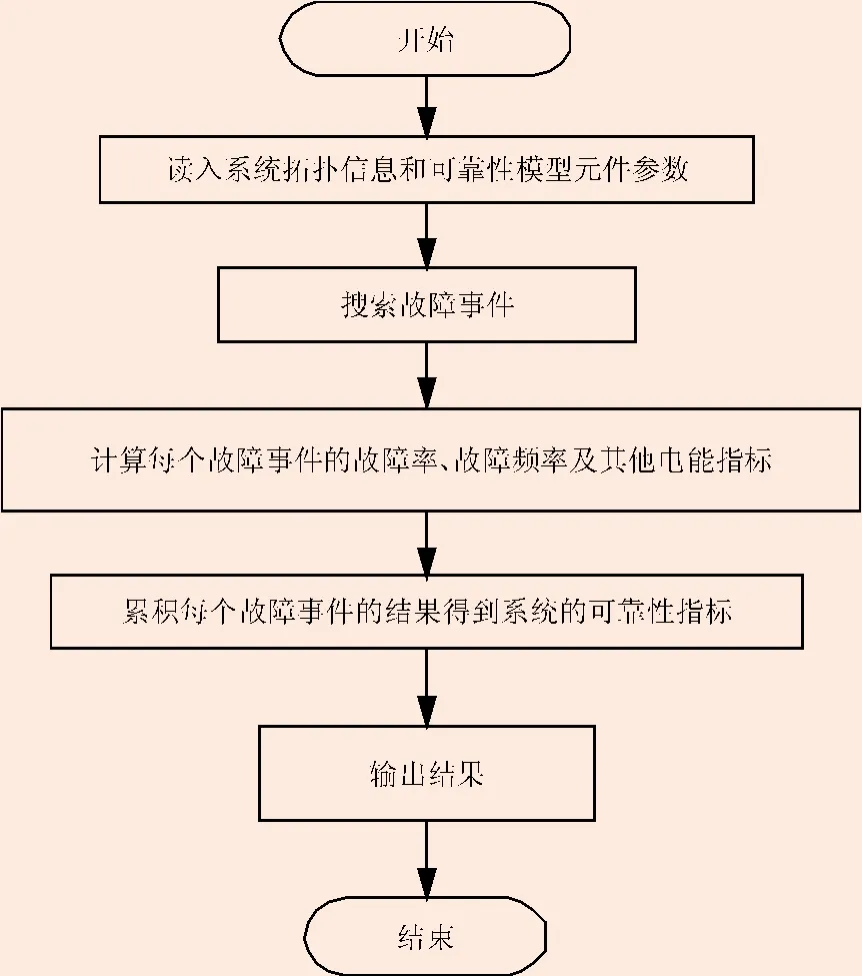
图1 电气主接线可靠性评估基本流程图

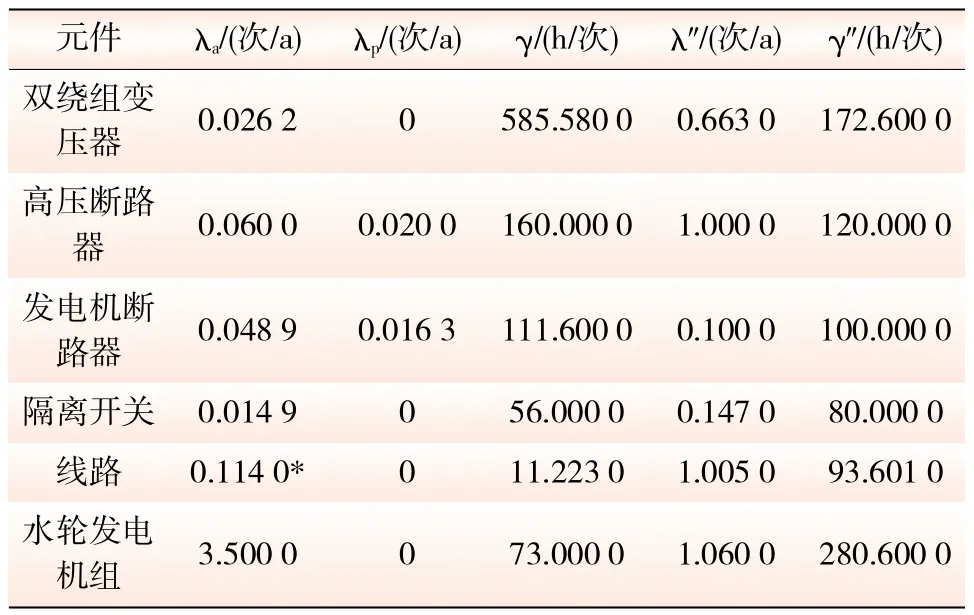
表2 元件可靠性原始数据

表3 断路器的不同年实际操作次数下的负荷停运指标

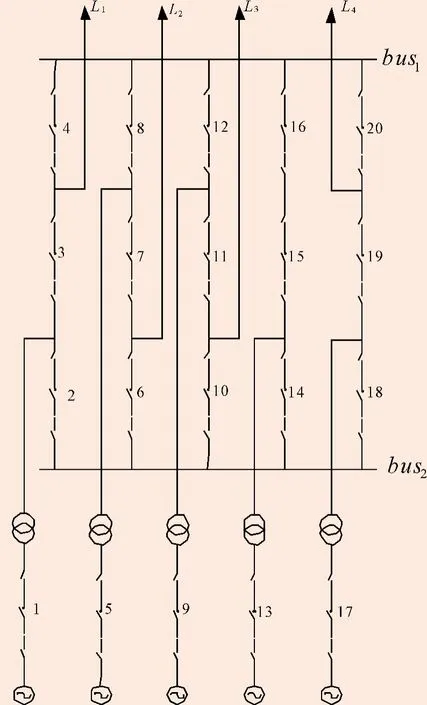
图2 2/3接线

4.1 不同的可靠性参数的影响

表3为断路器不同年实际操作次数下的负荷停运指标。图3、4为主接线灵敏度分析结果。

从表3中可以看出：断路器的动作次数对其故障率的影响很明显。由此可反过来证明，不考虑各种因素对断路器的故障率的修正，得到的结果是不精确的，误差很大，甚至可能会得出错误的结论，因此传统的电气主接线评估方法是不完善的。

4.2 灵敏度分析

根据系统可靠性指标对元件可靠性参数灵敏度的影响，做出LOLP、EENS随着某个位置断路器故障率变化而变化的曲线如图3、4所示。

图3 LOLP对断路器故障率的灵敏度

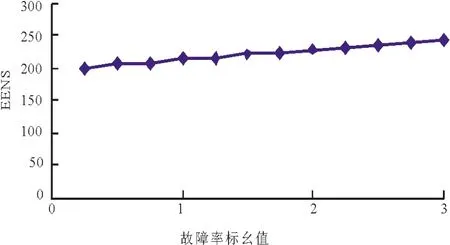
图4 EENS对断路器故障率的灵敏度

图3、4中横坐标为断路器故障率参数标么值，纵坐标为系统可靠性指标LOLP和EENS，从图3、4中可以看出断路器的故障率的改变对系统可靠性指标产生了明显的影响。当断路器故障率由0.25变化到3时，系统的LOLP指标由98%增加到130%，说明随着故障率参数的增加，系统的可靠性指标变化越来越明显。可靠性灵敏度指标可为工程人员的投资分析提供丰富的信息。

5 结语

本文密切结合水电站规划设计和电力运行部门的需要，对主接线可靠性的性能指标进行了分析。在对主接线可靠性计算分析中考虑了水电站的特性，如月平均出力，保证率曲线，电站年利用小时数等，并考虑了断路器开关动作次数对故障率模型的影响，以及线路侧和发电机侧断路器故障率高等特点。通过对断路器可靠性参数的灵敏度分析得出：断路器的的故障率对整个电站的可靠性有着至关重要的影响，加强对这部分元件的投资改进，可以明显改善整个系统的可靠性。

[1]刘海军,韩民晓,吴俊勇.基于最小割集的牵引变电站主接线可靠性评估[J].电网与清洁能源,2008,24（1）:24-29.

[2]鲁宗相,郭永基.水电站电气主接线可靠性评估[J].电力系统自动化,2001,25（18）:16-19.

[3]张鹏,郭永基.电气主接线可靠性评估的区间方法[J].电力系统自动化,2004,28（19）:48-52.

[4]冯怡,周家启.三峡电站电气主接线可靠性分析[J].电力系统保护与控制,2009,37（3）:21-26.

[5]BILLINTON R,CHEN H,ZHOU Jia-qi.Generalized n+2 State System Markov Modle for Station-oriented Reliability Evaluation[J].IEEE Trans on Power Systems,1997,12（4）:1511-1517.

[6]赵渊,周念成,谢开贵,等.大电力系统可靠性灵敏度分析[J].电网技术,2005,29（24）:25-30.

[7]郭永基.电力系统可靠性分析[M].北京:清华大学出版社,2002:162-206.

[8]吴开贵,吴中福.基于敏感度分析的电网可靠性算法[J].中国电机工程学报,2003，23（4）：53-56.

[9]袁亚华，王自果.最小路集的邻接终点矩阵算法[J].西北工业大学学报，1989，7（4）:473-478.

[10]王锡凡.发电厂主接线可靠性研究（一）[J].西安交通大学学报,1990,24（2）:31-40.

[11]王锡凡.发电厂主接线可靠性研究（二）[J].西安交通大学学报,1990,24（3）:31-38.

[12]电力系统可靠性评估[M].周家启，译.重庆:科学技术文献出版社重庆分社,1986.

[13]董百强,谢开贵,周家启.电站3/2接线和4/3接线的可靠性比较分析[J].重庆大学学报,2006,29（10）:10-15.

[14]WANG Xi-fan，WANG Xiu-li.Generalized Outage Table Approach to Reliability Study of Power Station’s Bus Schenes[J].IEEE Trans on Power Delivery.1997,12（4）：1480-1485.

[15]吴开贵，王韶，张安邦，等.基于RBF神经网络的电网可靠性评估模型研究[J].中国电机工程学报，2000,20（6）:9-12.