空间网格结构连续倒塌分析的瞬时移除构件法

丁 阳，葛金刚，李忠献

(1. 天津大学建筑工程学院，天津 300072；

2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072)

结构的连续倒塌是指结构在意外荷载(如地震、爆炸、撞击、火灾等)作用下局部产生损伤，导致产生结构单元失效的一系列连锁反应，继而发生局部或整体倒塌[1]．关于连续倒塌，学者们提出了很多分析方法和设计建议，并编制了分析与设计规程，如英国标准[2]、欧洲规范[3]、美国 GSA 和 DoD 发布的相关规程[4]等．在连续倒塌分析方法中，多传递路径法(又称拆除构件法)由于简单直接被广泛采用．多传递路径法主要过程为拆除结构中部分构件，模拟构件失效，分析剩余结构强度，判断结构是否发生连续倒塌；如发生连续倒塌，则通过增强拆除后的剩余构件强度来避免连续倒塌，从而提高结构抗连续倒塌能力[5]．

构件的失效过程是一个动态的过程，在瞬间失效期间剩余结构将进行内力、变形和刚度的重分布，产生明显的动力效应．同时连续倒塌伴随着强烈的几何非线性和材料非线性，因此考虑动力效应和双重非线性的动力分析被认为是较为合理准确的研究结构连续倒塌的分析方法．文献[6]针对单自由度分析模型，提出了 3种动力反应分析思路：瞬时刚度退化法、瞬时加载法及初始条件法．

无论使用多传递路径法还是文献[6]中提出的 3种方法对结构进行连续倒塌分析，均需首先假定结构失效构件位置和失效构件数量．与框架结构相比，大跨度空间网格结构，其杆件数量众多，通过移除某根或某几根杆件可能并不会引起结构的连续倒塌；且在地震等动力荷载作用下，杆件失效位置并不确定，随动力作用方向和大小的变化而变化．因此使用多传递路径法对大跨度空间网格结构进行连续倒塌分析将导致计算量庞大且效率较低．另外，多传递路径法未能考虑动力弹塑性效应、初始平衡态(初始应力、变形、刚度)对结构受到局部破坏后的影响以及偶然荷载作用对剩余结构构件造成的损伤，单纯只是移除构件来模拟失效，与实际情况存在明显差异．

为此，笔者采用显式中心差分法，以损伤累积为构件破坏准则，提出了实时删除失效构件的瞬时移除构件法．此方法无需假定构件失效位置及失效时刻，考虑了动力荷载作用下结构的几何非线性和物理非线性以及构件瞬时失效对剩余结构的动力效应．

1 破坏准则

采用合理的破坏准则是进行连续倒塌分析的前提．结构和构件的破坏准则目前主要有强度破坏准则、变形破坏准则、能量破坏准则、基于低周疲劳的破坏准则、基于最大变形和滞回耗能双重指标的破坏准则等[7-9]．文献[10]基于低碳钢试件在一维循环荷载作用下的滞回曲线和能量损伤理论，提出了预测钢结构及构件在地震作用下的损伤演化规律及计算方法．文献[11]在此基础上提出三维应力状态下钢材的损伤累积模型，即损伤

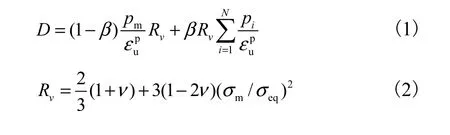
式中： pm为循环过程中最大等效塑性应变；pi为第i个加载半周期的等效塑性应变；为极限塑性应变；β为损伤权值；Rv为三轴应力因子，反映了三轴应力比的影响；ν为泊松比；σm为平均主应力；σij为应力张量．

随着材料损伤的不断累积，钢材的弹性模量ED、屈服强度σs,D也不断降低，可分别表示为[10]

式中：ED和 E0分别为损伤变量值等于D和0时对应的弹性模量值；s,Dσ和s0σ分别为损伤变量值等于D和0时对应的屈服强度；ξ1和ξ2分别为材料系数．

该损伤累积模型以试验为基础，同时考虑了最大塑性应变和循环滞回耗能的影响．笔者通过编写程序将此模型引入到材料本构模型中，并以此模型作为构件的破坏准则．

2 瞬时移除构件法

结构的连续倒塌属大变形动力非线性问题，使用隐式积分法求解存在收敛困难，因此基于显式积分法，提出了以损伤累积作为构件破坏准则，并实时删除失效构件，释放其内力的瞬时移除构件法．此方法考虑了构件瞬时失效对结构的动力效应，初始平衡态对结构受到局部破坏后的影响，偶然荷载作用对剩余结构其他构件造成的损伤．

根据有限单元法可知，节点处动力学平衡方程为[12]

瞬时移除构件法以中心差分法为基础，其主要过程如下所述．

(2) 根据中心差分法对式(7)进行积分，得

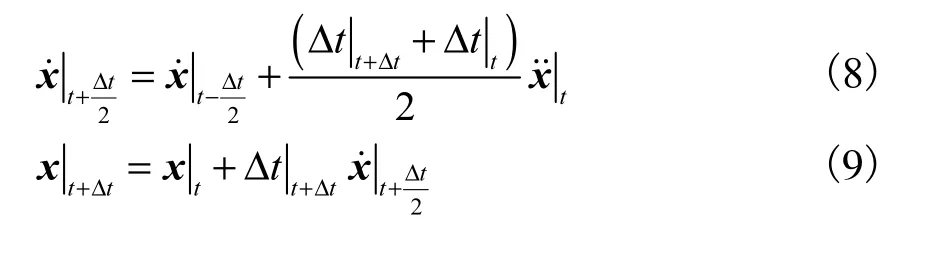
(3) 由式(9)可得单元应变增量dε，对于失效单元设置其应力σ=0，未失效单元根据考虑损伤累积的本构关系计算单元积分点处应力，即

(6) 设置时间t为t+Δt，返回步骤(1)．

3 方法验证

为验证本文中提出的瞬时移除构件法的正确性，分别应用本文方法和文献[6]提出的瞬时刚度法、瞬时加载法及初始条件法对图 1(a)所示双杆模型进行动力非线性分析，并对比节点 a的竖向位移．由于应用瞬时加载法及初始条件法时均需移除失效杆件，因此本文应用这两种方法进行对比分析时所用模型为图1(b)所示的悬臂梁．

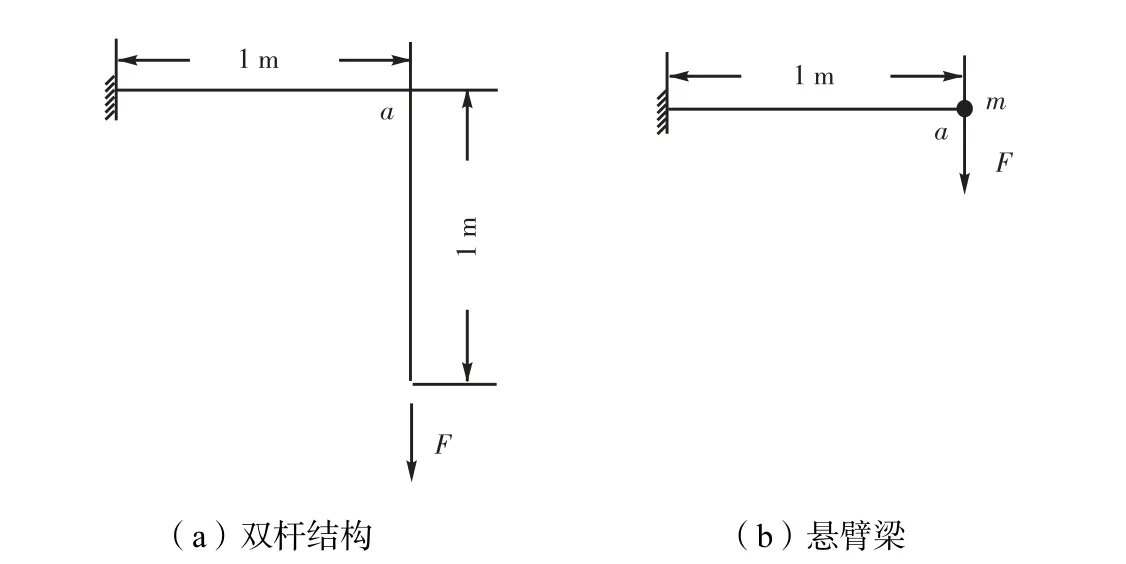
图1 结构计算模型Fig.1 Model for calculation of structure

有限单元法中空间梁单元模型定义空间梁质量平均分配于两端节点，为使模拟条件相同，在悬臂梁自由端施加集中质量，数值为竖向杆件质量的1/2．对比分析过程可简述为：①应用瞬时移除构件法对双杆模型进行分析，如图 1(a)所示，逐渐增大竖向荷载，直至竖向杆件失效并被移除，确定竖杆失效时所施加的荷载 F0、加载时间 t0及节点 a的竖向位移x0；②应用瞬时刚度法以图 2所示力的加载方式对双杆模型进行分析，当施加的荷载为 F0时，将竖杆刚度设置为0；③应用瞬时加载法以图2所示力的加载方式对悬臂梁进行分析，当施加的荷载为 F0时，在悬臂梁自由端施加与 F0大小相等、方向相反的竖向荷载；④应用初始条件法，以图 3所示位移的加载方式在悬臂梁自由端施加竖直向下的位移荷载，当所施加位移荷载为 x0时，瞬时移除所施加的位移荷载．采用以上4种分析方法分析节点a的位移，不同方法所得节点 a位移时程对比如图 4所示．对双杆结构进行分析时，为使竖向杆件先于横向杆件失效，横杆选取较大截面，竖杆选取较小截面，杆件截面分别为Φ245 mm×12 mm和Φ32 mm×2.5 mm．材料本构模型选用等向强化本构，杆件材料性能参数如表 1所示．阻尼采用 Reileigh阻尼，阻尼比取 0.02．应用本文方法分析时，竖杆损伤值变化如图5所示．

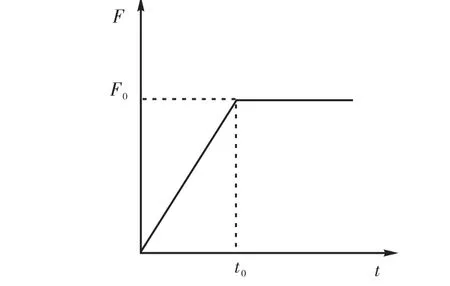
图2 力的加载方式Fig.2 Loading model of force

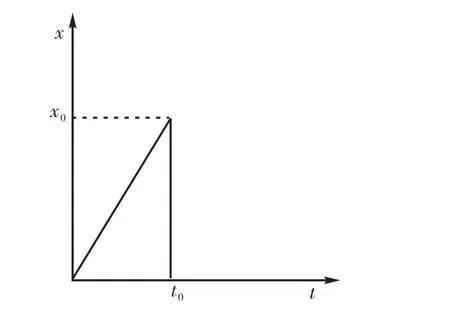
图3 位移的加载方式Fig.3 Loading model of displacement

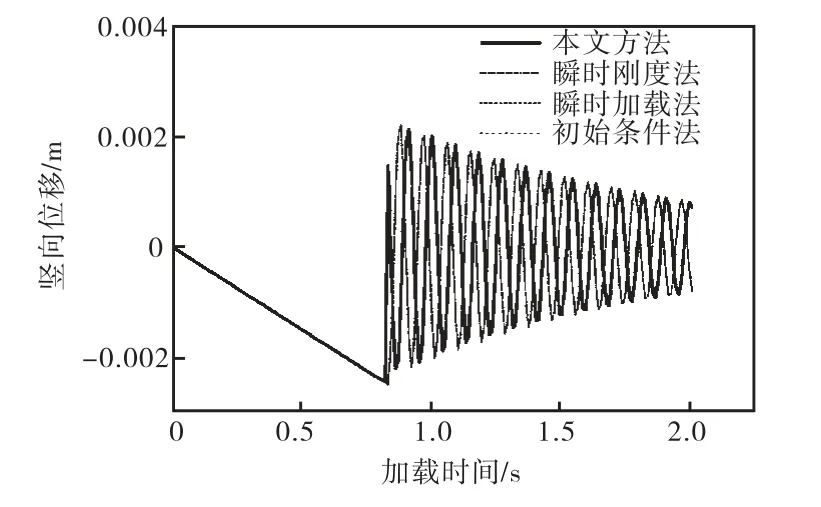
图4 节点a位移对比Fig.4 Comparison of displacement on node a

表1 杆件材料性能Tab.1 Material properties for member

由图 4可知，应用本文方法和文献[6]提出的瞬时刚度法、瞬时加载法及初始条件法分析时，节点 a位移最大值和衰减规律一致．由于文献[6]提出的分析方法未能考虑模型中竖杆损伤累积效应的影响，使得应用文献[6]提出的分析方法所得节点 a振动初相位滞后于应用本文方法所得结果．由图 4和图 5可知，应用本文方法分析时，加载过程中，竖杆经历损伤的不断累积，当损伤累积至一定程度后，损伤值 D突然增大，竖杆刚度迅速降低．当竖杆损伤值 D＝1时，竖杆失效并被“移除”，节点 a有阻尼自由振动，位移逐渐衰减．

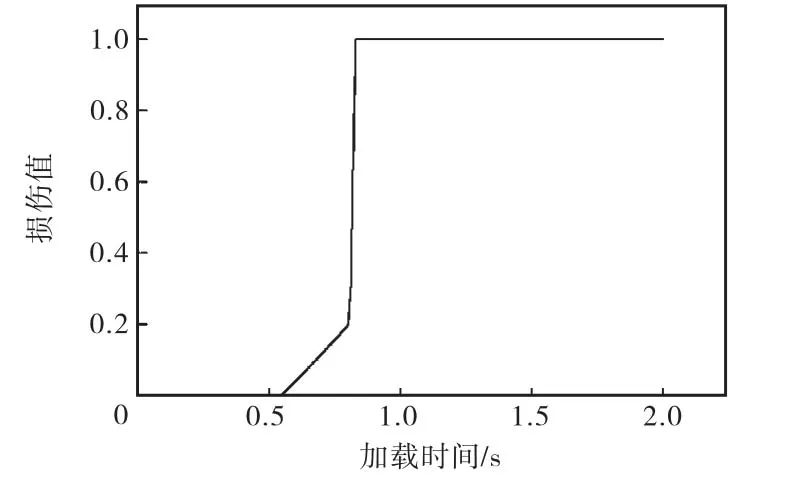
图5 竖杆损伤值Fig.5 Damage of vertical member

通过分析可知，采用本文提出的瞬时移除构件法能够很好地模拟杆件失效后结构的动力行为，且能够考虑杆件损伤累积对周围杆件的影响．

4 空间网格结构算例分析

4.1 圆钢管稳定判别条件及恢复力模型

不考虑杆件失稳效应将高估结构承载力．本文中采用国际标准化组织[13]根据大量圆钢管试验结果归纳出的空间受力圆钢管的稳定判别方程，即

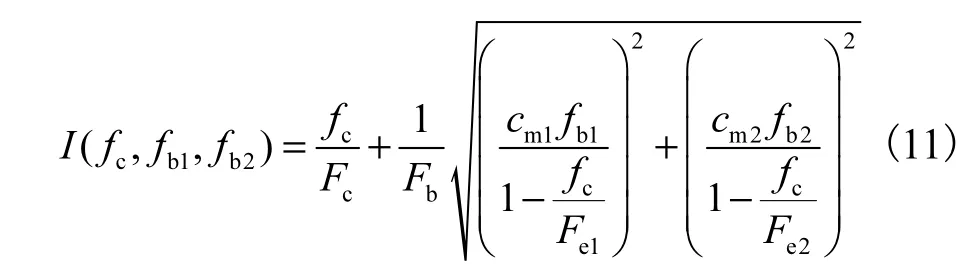
试验研究[14]表明，杆件受压失稳后承载力降低，反向加载未拉直前不能完全工作．Marshall模型[15](图 6)是根据圆钢管试验所得滞回曲线总结而成，描述了包含初始缺陷的非弹性杆件的滞回性能以及受压失稳后轴向刚度的下降．本文采用此模型模拟杆件失稳后的性能．

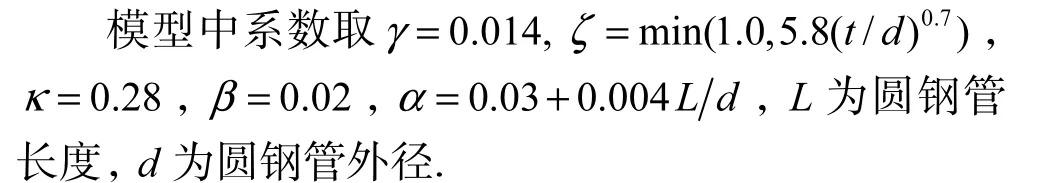
图6 Marshall模型Fig.6 Marshall model

计算过程中假定杆件截面面积不变，则图6所示的 Marshall模型中轴向力与轴向应变的关系可转变为轴向应力与轴向应变的关系．将圆钢管稳定判别公式和转变后的 Marshall模型通过编写程序引入到考虑损伤累积的材料本构模型中，从而模拟圆钢管失稳及失稳后行为．

4.2 算例分析

为检验瞬时移除构件法在空间网格结构连续倒塌分析中的适用性，考虑杆件失稳效应影响，应用瞬时移除构件法对地震作用下单层柱面网壳进行连续倒塌分析．网壳长度为27,m，宽度为15,m，矢宽比为1/3，屋面均布荷载为2.0,kN/m2，杆件截面取Φ89,mm×4,mm 和 Φ140,mm×6,mm，斜杆选用较大截面，纵杆和端杆选用较小截面．支座形式为四边支承．杆件材料性能如表1所示．《建筑抗震设计规范》(GB50011—2001)[16]规定，设防烈度为 8度(0.30,g，g 为重力加速度)罕遇地震时，时程分析所用地震波加速度幅值取510,cm/s2，选用时长为20,s的El-Centro (1940)波，按8度(0.30,g)罕遇地震设防烈度调整地震波幅值．地震波采用三向输入，输入比值为1∶0.85∶0.65．

由计算可知，地震作用起始阶段，由于地震加速度较小，网壳结构杆件均处于弹性状态，未发生损伤．随地震作用的不断增强，网壳结构中杆件受力逐渐增大，部分受压杆件发生失稳．在地震作用的第7.42,s，网壳结构中首次出现失稳杆件(197号杆件)，所在位置如图 7所示(数字为杆件编号)．由于地震作用的不断变化，失稳杆件位置及数量也在不断变化．由于杆件在受压失稳及受拉屈服后均产生塑性变形，发生损伤，因此杆件的损伤值也由二者叠加而成，且损伤程度随地震的不断作用而增加．在地震作用的第13.07,s，网壳结构首先出现损伤变量D＝1的杆件(182号杆件)，所在位置如图 7所示．根据瞬时移除构件法，当杆件损伤变量 D＝1时，其应力将被设置为 0，此时杆件被“移除”，其所承担的内力突然释放，结构内力和刚度将进行重分配．随着地震作用时间的增加，损伤区域以失效杆件为中心，逐渐向周围扩大，失效杆件数量增多．不同杆件失效时刻如表2所示，失效位置如图7所示．

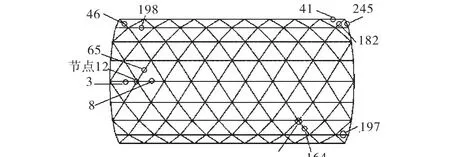
图7 网壳结构杆件失效位置Fig.7 Location of member failure in reticulated shell

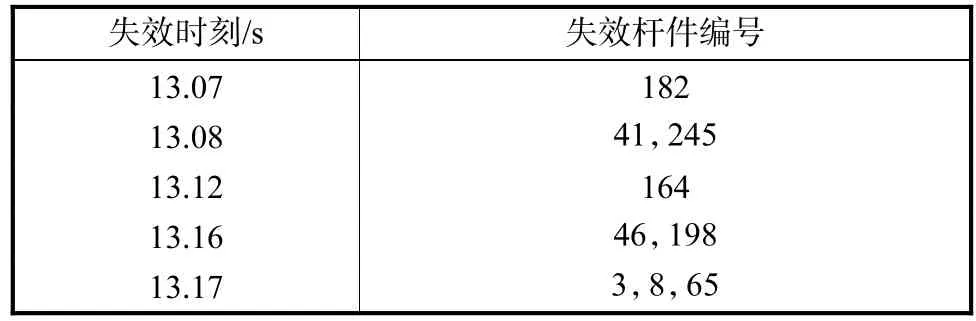
表2 杆件的失效顺序Tab.2 Order of member failure

为观察杆件失效时的应力变化及杆件失效对其相连节点的影响，给出了164号杆件轴向应力时程曲线和与其相连的67号节点位移时程曲线，如图 8和图9所示．

由图8和图9可知，当164号杆件损伤变量D＝1时，其应力将被设置为 0，以模拟杆件失效．由于164号杆件的突然失效，与其相连的 67号节点由于所受合力的改变，位移也将发生跳跃．随后由于与67号节点相连的其他杆件无法继续承担地震的继续作用，67号节点位移发散．

由表2和图7可知，地震作用下，单层柱面网壳杆件失效区域主要分布于沿长度方向的两侧，且单根杆件的失效并不会引起网壳结构的倒塌．地震作用第 13.17,s时，网壳结构由于失效杆件过多，节点 12最大位移和网壳结构的应变能突然增大(如图 10和图 11所示)，网壳结构倒塌破坏，倒塌破坏过程中变形如图12所示．

图8 164号杆件轴向应力Fig.8 Axial stress of members No.164

图9 67号节点位移Fig.9 Displacement in node 67

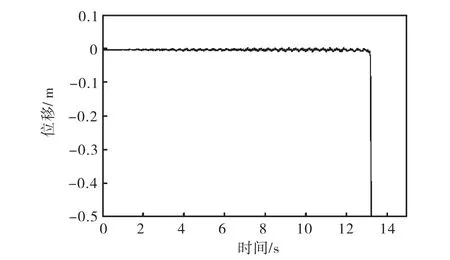
图10 节点12位移时程Fig.10 Displacement in node 12

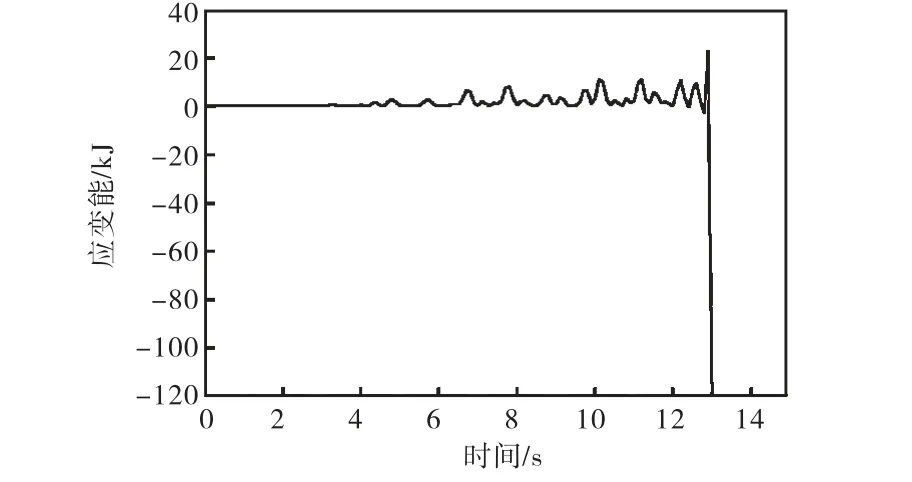
图11 结构应变能Fig.11 Strain energy of structure

由算例分析可知，以损伤累积为破坏准则的瞬时移除构件法，能够同时考虑几何非线性和物理非线性，在地震等动力荷载作用下根据杆件损伤情况判断失效杆件位置和失效时刻，且考虑了杆件瞬时失效对剩余结构的动力效应，可应用于空间网格结构的连续倒塌分析．

图12 结构倒塌变形Fig.12 Collapse deformation of structure

5 结 论

(1) 采用显式中心差分法，以损伤累积为破坏准则，提出了用于结构连续倒塌分析的瞬时移除构件法；对比相同加载方式下双杆模型和悬臂梁节点位移，验证了本文提出的瞬时移除构件法的正确性．

(2) 考虑材料非线性、几何非线性、杆件失稳及失稳后性能，对单层柱面网壳进行连续倒塌分析，结果表明瞬时移除构件法可用于空间网格结构的连续倒塌分析．

［1］ Marjanishvili S M. Progressive analysis procedure for progressive collapse[J].Journal of Performance of Constructed Facilities，ASCE，2004，18(2)：79-85.

［2］ British Standard Institute. Structural Use of Concrete：(Part 1)：Code of Practice for Design and Construction[S]. 1997.

［3］ European Committee for Standardization. Eurocode 1：Actions on Structures[S]. 2002.

［4］ Department of Defense. Design of Buildings to Resist Progressive Collapse[S]. 2005.

［5］ 陆新征，李 易，叶列平，等. 钢筋混凝土框架结构抗连续倒塌设计方法的研究[J]. 工程力学，2008，25(SupplⅡ)：150-157.

Lu Xinzheng，Li Yi，Ye Lieping，et al. Study on design method to resist progressive collapse for reinforced concrete frames[J].Engineering Mechanics，2008，25(SupplⅡ)：150-157(in Chinese).

［6］ Nanci B，Shalva M. SDOF model for progressive collapse analysis[C]//New York：Structures，ASCE，2005：2243-2254.

［7］ Sidney A G，Erber T，Stefanis J，et al. Plastic collapse，shakedown and hysteresis of multistory steel structures[J].Journal of Structural Engineering，1986，112(12)：2610-2627.

［8］ Darwin D，Nmai C K. Energy dissipation in RC beams under cyclic load[J].Journal of Structural Engineering，1986，112(8)：1829-1846.

［9］ 杜修力，欧进萍. 建筑结构地震破坏评估模型[J]. 世界地震工程，1991(3)：52-58.

Du Xiuli，Ou Jinping. Evaluation model of earthquake damage for building[J].World Earthquake Engineering，1991(3)：52-58(in Chinese).

［10］ Shen Zuyan，Dong Bao. An experiment-based cumulative damage mechanics model of steel under cyclic loading[J].Advances in Structural Engineering，1997，1(1)：39-46.

［11］ 宋振森. 超高层钢结构考虑损伤和损伤累积分析方法[D]. 上海：同济大学土木工程学院，2004.

Song Zhensen. Research on Analysis Methods for Super High-Rise Steel Structure Considering Damage Accumulation[D]. Shanghai：College of Civil Engineering，Tongji University，2004(in Chinese).

［12］ 庄 茁，张 帆，岑 松，等. ABAQUS非线性有限元分析实例[M]. 北京：科学出版社，2005.

Zhuang Zhuo，Zhang Fan，Cen Song，et al.Examples of Nonlinear Finite Element Analysis in ABAQUS[M]. Beijing：Science Press，2005(in Chinese).

［13］ ISO10721-1 Steel Structure：Material and Design[S].1997.

［14］ Higginbotham A B，Hanson R H. Axial hysteretic behavior of steel members[J].Journal of the Structural Division，ASCE，1976，102(7)：1365-1381.

［15］ Marshall P W，Gates W E，Anagnostopoulos S. Inelastic dynamic analysis of tubular offshore structures[C]//Proceedings of Ninth Annual Offshore Technology Conference. Houston，USA，1977：235-246.

［16］ 中华人民共和国建设部. GB50011—2001 建筑抗震设计规范[S]. 2001.

Ministry of Construction of the People's Republic of China. GB50011—2001 Code for Seismic Design of Buildings[S]. 2001(in Chinese).