测量机滚珠丝杠Z轴伺服系统的动力学建模及补偿

向红标，裘祖荣，李醒飞，谭文斌，张晨阳

(1. 天津大学精密测试技术及仪器国家重点实验室，天津 300072；2. 天津商业大学机械工程学院，天津 300134)

测量机滚珠丝杠Z轴伺服系统的动力学建模及补偿

向红标1，裘祖荣1，李醒飞1，谭文斌1，张晨阳2

(1. 天津大学精密测试技术及仪器国家重点实验室，天津 300072；2. 天津商业大学机械工程学院，天津 300134)

在对θFXZ型测量机 Z轴伺服系统的机械结构和控制系统进行分析的基础上，建立了伺服系统的动力学模型.根据受力分析，对系统的干扰力进行建模.利用对PID参数的自适应调节和干扰力的前馈补偿，实现对系统的误差补偿.实验结果表明，补偿后的跟踪误差约为补偿前的1/4，系统静差也由原来的2 μm减小到0.4 μm以内.该伺服系统的动力学建模和干扰力建模能直观、有效地描述Z轴系统的运动特性，补偿方案能很好地改善系统的动态跟踪误差和控制定位精度.

伺服系统模型；干扰力模型；跟踪误差；静差

伺服系统作为坐标测量机(coordinate measuring machine，CMM)的重要功能部件，其动静态特性是影响坐标测量机性能和精度的重要指标之一.而伺服系统的性能与很多因素有关，如机械传动方式、系统机械刚度和负载、检测元件的精度、系统各项控制参数、非线性摩擦力以及外部干扰等.因此，建立伺服系统的动力学模型有助于更深入地研究伺服系统的特性，并通过各种补偿方法使其发挥出最佳性能.

θFXZ型[1]坐标测量机，由于滑架重量较轻，为使结构设计简单化，未在 Z轴设置重力平衡系统[2]，所以Z轴电机在驱动滑架进行上下运动时，不仅受到非线性摩擦力[3-4]的影响，同时还受到滑架重力的影响，这 2种干扰力均会影响到 Z轴伺服系统的动静态性能.为此，本文针对 θFXZ型坐标测量机的 Z轴运动系统，建立了伺服系统的动力学模型和干扰力模型，基于这些模型设计了控制系统的误差补偿方案，并通过实验验证了该补偿方案的有效性.

1 测量机结构

θFXZ型坐标测量机的基本结构见图 1，包括底座、立柱、滑架、转台和接触测头.实际工作中，转台带动工件转动，立柱作X向移动，滑架沿立柱作Z向移动，实现测头对工件的测量.

图1 θFXZ型坐标测量机结构Fig.1 Structure of θFXZ-type CMM

2 Z轴伺服系统的动力学建模

一般伺服系统由机械传动部分和控制部分组成，而伺服系统整体性能的好坏不仅与两部分各自的性能有关，更是由两部分的协调性决定，所以在设计高性能的伺服系统时，必须考虑这两部分之间的内在关系，建立准确、可靠的数学模型[5].

2.1 Z轴控制系统

控制系统由工业控制计算机(industrial personal computer，IPC)、PMAC 运动控制器、交流伺服电机、光栅尺(分辨率为 0.2,µm)以及接口电路组成，它以PMAC控制器为核心实现对伺服系统的控制，还具有对运动信号的采样处理、误差计算、误差补偿等功能.实验平台采用全闭环控制，图2为伺服系统的结构框图，位置环、速度环、电流环 3环控制如图所示，PMAC采用PID+速度/加速度前馈对位置环进行控制，交流伺服驱动器采用PI调节器对速度环进行控制.

图2 伺服控制系统的结构示意Fig.2 Structure sketch of servo control system

2.2 Z轴的机械传动机构与受力分析

如图 3所示，电机通过联轴节驱动滚珠丝杠旋转，再由滚珠丝杠螺母副带动滑架沿直线导轨运动，将旋转运动转换为直线运动.可将滑架及侧头支架部分简化为质量为Mg的工作台.

伺服系统的机械特性如刚度、惯量等对系统的优化设计有着重要的影响，需考虑这些因素来建立伺服系统的模型.通常伺服系统把电机和负载作为一个刚体即单质量伺服系统考虑，它与实际特性有一定的差别，实际系统中，在电机驱动力矩的作用下，机械传动部分会受到一定程度的变形，特别是加速度要求大、快速性和精度要求高的系统，弹性变形对系统的影响不能忽略.根据对该机械结构的计算分析，由滚珠丝杠扭转变形对滑架直线位移的影响，相对柔性联轴节的扭转变形和滚珠丝杠的轴向拉压变形对滑架直线位移的影响可忽略不计，设柔性联轴节扭转刚度为K1，滚珠丝杠的综合轴向传动刚度为K2.

图3 Z轴伺服系统结构示意Fig.3 Block diagram of Z-axis servo system

该测量机立柱伺服系统结构如图3所示.考虑结构受到的总摩擦力为Ff，包含有电机和滚珠丝杠传动摩擦力和导轨的摩擦力，可得动力学方程[6-7]为

式中：JM、JA和 JL分别为电机转子、联轴节和滚珠丝杠的转动惯量；Mg为滑架的质量；θM、θA分别为电机和联轴节的转角；Mθ˙、Aθ˙为与之相应的转角加速度；z、z˙为滑架Z向位移量和加速度；T和TM分别为电机的驱动转矩和通过联轴节传递给丝杠的主动力矩；Fd和 Ff分别为电机对滚珠丝杠的轴向驱动力和滑架受到的总摩擦力；Ks为旋转角度和位移的换算系数；L0为丝杠导程；η为滚珠丝杠效率.

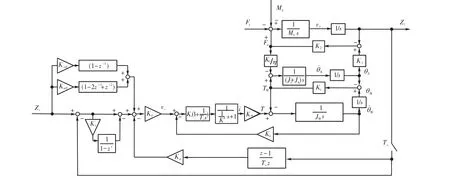
图4 Z轴伺服系统模型Fig.4 Z-axis servo system model

2.3 Z轴伺服系统建模

由以上动力学方程得出基于 PMAC运动控制器的 Z轴伺服系统的数学模型，如图 4所示.图中，Zc为指令位移量，Zt为实际位移量，vi为指令速度，vz为实际速度.三环伺服控制系统中，电流环可以等效为一阶惯性环节，1/K′为惯性环节的时间常数，Km为电机扭矩常数；Ti和 Kv分别为速度环的积分控制常数和比例，Kw为速度环反馈系数；PMAC为位置环提供了 PID+速度/加速度前馈的控制环算法，Kp、Ki、Kd分别为比例、积分、微分增益，Kvff和 Kaff分别为速度和加速度前馈增益.

3 Z轴干扰力建模

3.1 干扰力模型描述

在高精度高性能的伺服系统中，由于非线性摩擦力的存在，对系统的动静态性能产生了很大影响.Stribeck摩擦模型[8]是一种常用的能够反映摩擦非线性特性的摩擦模型，表述为

式中：Fs为最大静摩擦力；Fc为库仑摩擦力；B为黏性摩擦系数；vs为临界速度；δ为经验参数，本文中δ取2[9].在稳态时，摩擦力与速度的对应关系为Stribeck曲线，如图5所示.

由于实际模型参数还与运动方向有关，所以向上向下2个方向对应着不同的摩擦参数，当v＞0时，模型参数为、、B+；当 v＜0时，模型参数为、、B-.

图5 Stribeck曲线Fig.5 Stribeck curve

把重力和摩擦力的合力称为干扰力Fi，即得出干扰力模型为

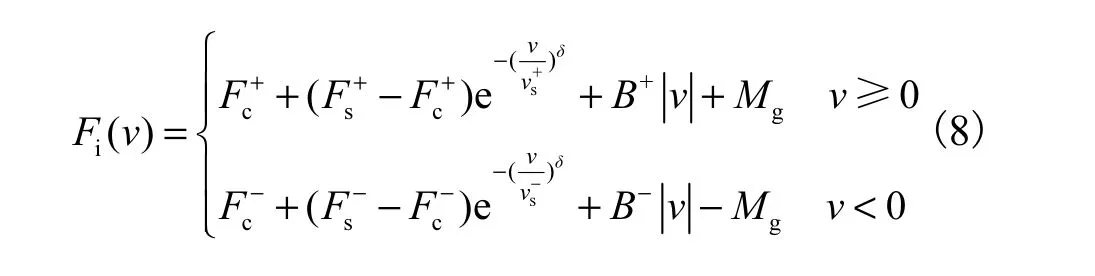
3.2 干扰力模型参数辨识

Stribeck摩擦模型参数辨识[10]的方法是根据稳态下摩擦力与速度的关系曲线，拟合零速附近阶段点的切线和高速阶段点的直线，低速切线与纵轴交点值为最大静摩擦力Fs，高速直线与纵轴交点值为库仑摩擦力 Fc，其斜率为黏性摩擦系数 B，低速直线与 F＝Fc直线交点的横坐标值即为临界速度 vs.而 Z轴干扰力模型辨识与Stribeck辨识方法基本一致.

由式(5)可知，当滑架作匀速直线运动(即z˙＝0)时，则有

式中：Fi为干扰力；Fd为驱动力.因此，通过测得多组稳态时速度 v与驱动力 Fd的数值，可得干扰力与速度的对应关系，如图6所示.其中，驱动力Fd的数值在每组匀速运动中有很小的波动，对其进行了平均值处理.图 6中左侧纵坐标为电机驱动力与速度曲线的纵坐标，右侧纵坐标为 Stribeck曲线的纵坐标，可以看出电机驱动力与速度曲线相当于是 Stribeck曲线向上平移了 Mg个单位.通过上述参数估计方法，可得本实验系统的干扰力模型参数如表1所示.

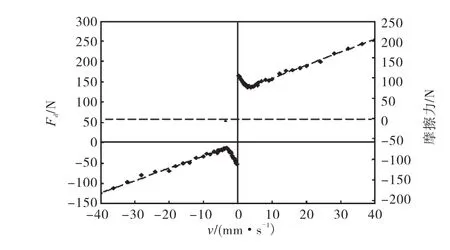
图6 驱动力与速度关系曲线Fig.6 Driving force and velocity curve

表1 正负向运动的干扰力模型参数Tab.1 Identified disturbing force model parameters

4 Z轴补偿实验

测量机Z轴结构不仅受到摩擦力的影响，还受到滑架自身重力影响，所以电机驱动滑架向上和向下运动时负载区别很大.考虑这些因素，需要先针对运动方向和运动速度设定相应的 PID参数，然后再对 Z轴干扰力进行前馈补偿.

4.1 补偿前实验现象

运动控制器 PMAC配套软件 PEWIN具有强大的数据采集功能，利用该软件可实现对系统指令、实际运动信息(包括位置、速度和加速度信息)以及位置跟踪误差的采集，得到相关的数据曲线.

当系统采用普通的 PID控制执行一次上下往返运动时，通过 PEWIN采集相关的运动信息，可得到速度和跟踪误差的曲线如图 7和图 8所示.该运动的期望参数为：速度 2,mm/s，加速时间 100,ms，位移2,mm.可以看出，向上和向下运动在速度过零点时，跟踪误差波形会发生畸变，出现尖峰现象，其主要原因是由于Z轴受到干扰力的影响.

图7 往返运动的速度曲线Fig.7 Velocity curve of to-and-fro movement

图8 往返运动的跟踪误差曲线Fig.8 Following error curve of to-and-fro movement

4.2 补偿方案

高精度高性能的伺服控制系统必须具有良好的刚性和快速的响应速度，但由于负载和速度的变化，很大程度上影响了系统的精度和性能，这就要求系统的PID参数具有一定的自适应调节能力，经调试本文分别针对 2个方向在不同速度范围设定了合适的PID参数，使控制性能和系统刚性达到最佳，同时对干扰力进行前馈补偿，2个方面有效地减小了系统的跟踪误差和静差.

本系统的补偿实验是通过 PMAC控制器嵌入PLC程序实现的，其流程如图9所示，PLC程序以极高的采样速率监视系统运动速度方向和大小，从而判断采用何种PID参数，并根据速度的大小和方向实时计算出干扰力大小，并将其值赋给前馈补偿变量，从而实现对 Z轴误差的补偿.干扰力的前馈补偿模型如图 10所示.图中，Gm(z)为机械部分的传递函数，Gv(z)为速度环的 PI控制器，Gp(z)为位置环的 PID控制器，Gf(z)为干扰力前馈补偿函数.

图9 PLC程序流程Fig.9 Flow chart of PLC program

图10 干扰力的前馈补偿模型Fig.10 Model of feed-forward compensation for disturbing Fig.10 force

4.3 补偿实验结果与分析

针对上述期望运动，首先分别根据速度选择向上和向下运动的最佳 PID参数，并通过 PLC程序对PID和干扰力变量参数进行赋值，从而实现前馈补偿.由于速度和加速度的设定对系统的响应性能影响较大，该补偿实验对系统的动态误差和静差均有明显改善，本文以低速和高速2种运动程序为例来说明其补偿效果.

(1)运动控制程序 1：以速度±2,mm/s，加速时间100,ms，位移 2,mm 为运动参数，其补偿前后误差曲线如图11所示.由图 11可知，补偿后的动态跟踪误差明显小于未补偿段的跟踪误差，最大跟踪误差值由10,µm 减小到 2,µm，约为未补偿的 1/4.系统的静差也由原来的 2,µm 减小到 0.4,µm.

图11 运动控制程序1跟踪误差曲线Fig.11 Following error curves of motion program 1

图12 运动控制程序2跟踪误差曲线Fig.12 Following error curves of motion program 2

(2)运动控制程序 2：以速度±100,mm/s，加速时间 50,ms，位移 20,mm 为运动参数，得到补偿前后误差曲线如图 12所示.可以看出，补偿实验也有效地减小了系统的跟踪误差和静差，最大跟踪误差值由110,μm 减小到 40,μm，静差由原来的2,μm 减小到0.4,μm，系统性能得到很大程度的改善，但在加速和减速时补偿段还有一定的尖峰出现，这主要是因为传动环节在加减速过程中，受到较大的控制力矩，会导致传动环节有一定程度的弹性变形，此时只有采用对滚珠丝杠和导轨加压的方式来提高系统的机械刚性，或采取其他如直线电机传动的机械传动方式，才能进一步减小系统的跟踪误差.

5 结 语

本文针对θFXZ型测量机Z轴运动系统，建立了伺服系统的动力学模型和干扰力模型，采用 PLC程序实现对 PID参数的自适应调节和干扰力的前馈补偿，有效地降低了伺服系统的跟踪误差和静差.补偿后的系统静差由原来的2,µm减小到0.4,µm 以内，跟踪误差也约为补偿前的 1/4.对该系统的动力学建模和干扰力建模能直观、有效地反映Z轴系统的运动特性，补偿方案能很好地改善系统的动态跟踪误差和控制定位精度，适用于未在Z轴设计平衡系统的装置.

［1］张国雄. 三坐标测量机[M]. 天津：天津大学出版社，1999.

Zhang Guoxiong.Coordinate Measuring Machines[M].Tianjin：Tianjin University Press，1999(in Chinese).

［2］Dein Shaw，Ou Guanyin. Reducing X，Y and Z axes movement of a 5-axis AC type milling machine by changing the location of the work-piece computer-aided design[J].CAD Computer Aided Design，2008，40(10)：1033-1039.

［3］Israelachvili J.Intermolecular and Surface Forces[M].New York：Academic，2005.

［4］Rabinowicz E.Friction and Wear of Materials[M]. New York：Wiley，2005.

［5］祁若龙.开放式数控伺服模型及位置控制技术的研究[D]. 大连：大连理工大学机械工程学院，2008.

Qi Ruolong. Research on Open CNC Servo System Model and Position Control Technology [D]. Dalian：School of Mechanical Engineering，Dalian University of Technology，2008(in Chinese).

［6］Xiang Hongbiao，Qiu Zurong，Li Xingfei. Simulation and experimental research of non-linear friction compensation for high-precision ball screw drive system[C]//Proceedings of 9th International Conference on Electronic Measurement and Instruments.Beijing，China，2009：3604-3609.

［7］Itoh K，Iwasaki M，Matsui N. Robust fast and precise positioning of ball screw-driven table system on machine stand[C]//8thIEEE International Workshop on Advanced Motion Control. 2004：511-515.

［8］Stribeck R. Die wesentlichen eigenschaften der gleit-und rollenlager：The key qualities of sliding and roller bearings[J].Zeitschrift des Vereins Deutscher In-genieure，1902，46(38/39)：1342-1348，1432-1438.

［9］张从鹏，刘 强. 直线电机定位平台的摩擦建模与补偿[J]. 北京航空航天大学学报，2008，34(1)：47-50.Zhang Congpeng，Liu Qiang. Friction modeling and compensation of positioning stage driven by linear motors[J].Journal of Beijing University of Aeronautics and Astronautics，2008，34(1)：47-50(in Chinese).

Dynamic Modeling and Compensation for the Ball Screw Z-Axis Servo System of Measuring Machine

XIANG Hong-biao1，QIU Zu-rong1，LI Xing-fei1，TAN Wen-bin1，ZHANG Chen-yang2
(1. State Key Laboratory of Precision Measuring Technology and Instruments，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Tianjin University of Commerce，Tianjin 300134，China)

A dynamic model was built on the basis of mechanical structure and the control system of Z-axis servo system of θFXZ-type coordinate measuring machine.Then the disturbing force model was built by force analysis.Finally，through the PID parameters′ adaptive adjustment and feed-forward compensation for disturbing force，the error compensation of the system was carried out. The experimental results show that the following error after compensation is four times less than that before compensation，and the static error of the system after compensation decreases from 2.0 μm to 0.4 μm. In a word，the servo system dynamic model and disturbing force model can intuitively and effectively describe the movement characteristics of Z-axis system. Furthermore，the compensation method can improve the following error of the system and the positioning accuracy.

servo system model；disturbing force model；following error；static error

TP273

A

0493-2137(2011)04-0291-06

2010-06-12；

2010-08-13.

国家自然科学基金资助项目（50975206/E050501）.

向红标（1982— ），男，博士研究生，xhb@tju.edu.cn.

李醒飞，lixf@tju.edu.cn.