基于形式概念分析的多光谱遥感影像波段选择
杨磊,刘智,王番,王刚,魏德强
(信息工程大学测绘学院,河南 郑州 450052)
1 引言
波谱信息作为影像信息的主要内容,为影像处理、分析、解译提供了重要的定量信息[1]。多光谱遥感影像拥有众多波段并包含大量的波谱信息,但由于其波段之间具有较强的相关性,导致很多信息重复或冗余。如果不加分辨地使用全部波段进行遥感影像分类或目标识别,不仅会增加计算量,还会影响处理精度和效果。这种影响可以通过降低波段维数得到有效地抑制,即在特征选择时,如何从数十甚至上百个波段中选择最佳波段,尽量减少冗余特征,在损失光谱信息尽量少的情况下准确、完整地表达光谱特征,成为一个值得研究的问题。
传统意义上数据降维可以用波段选择和线性变换来实现,其中经典的方法有主成份分析法(PCA)、K-L变换(缨帽变换)等,但这些方法也不同程度存在一些缺陷,比如线性变换法按照一定的规律旋转图像光谱空间坐标系来突出主要分量,达到压缩数据的目的,虽然速度很快,但是改变了图像的特性。本文提出的方法是在遥感图像处理中引入形式概念分析的思想,将多光谱影像看成一个形式背景,以各个波段作为形式属性,通过选择核心属性达到最佳波段选择的目的,实现数据降维。该方法与其他方法相比,不仅更简洁高效,而且在不改变图像特性的前提下更直观。最后,通过遥感影像分类验证了使用选择出的最佳波段比使用全波段的效果更好。
2 形式概念分析
形式概念分析(Formal Concept Analysis,简称FCA)是由德国数学家Wille R.于1982年提出的一种基于概念的数据挖掘和知识获取的数学方法。作为应用格理论的一个分支,概念格理论通过对象和属性之间的对应关系直观生动地表达了概念之间的泛化和特化的关系。张文修教授、魏玲博士等人提出了概念格的属性约简理论[2]。通常意义下的属性约简就是在不改变形式背景的概念结构和层次的前提下寻求最简化的属性集,用这个属性集表示的概念格与用所有属性表示的概念格同构[3-6]。
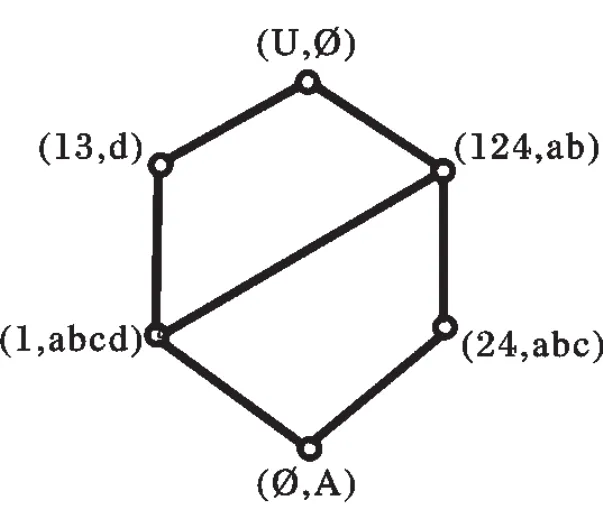
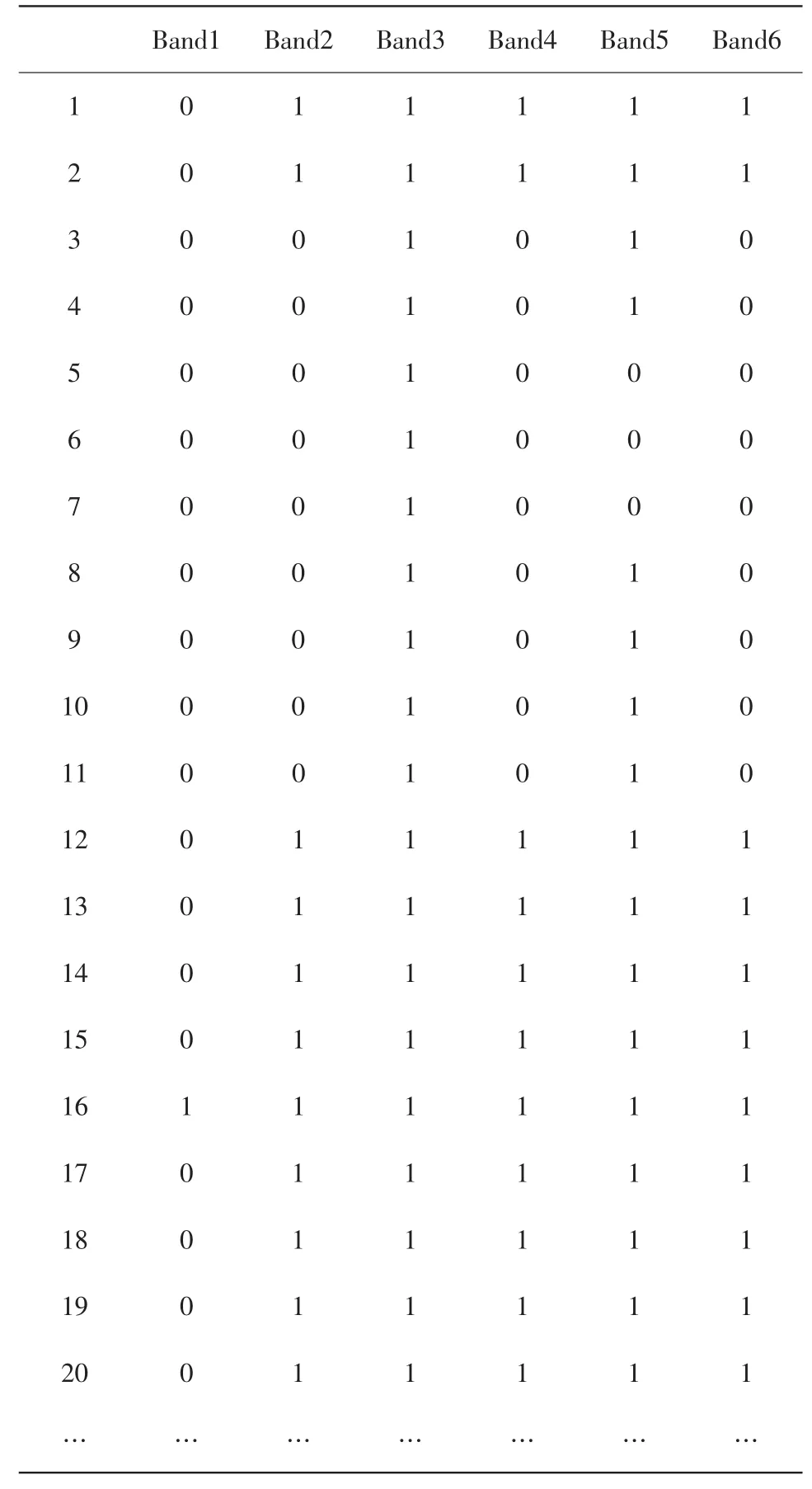
定义1.1形式背景[2]:一个形式背景可表达为一个三元组Κ(U,A,I),其中U和A是两个有限集,U={x1,x2,x3,…,xn}为对象集,U的元素xi(i 一个形式化的背景可以表示成一个交叉表,比如一个形式背景中:对象集U={1,2,3,4},属性集A={a,b,c,d,e},I表示对象具有属性,则对应的表如下: 表1.1 形式背景表Tab1.1 The Formal Context 定义1.2[2]:设X、B分别是对象集合U和属性集合A的子集。我们定义: f(X)={a∈A|坌x∈X,xIa}(A中对象共同属性的集合); g(B)={x∈U|坌a∈B,xIa}(具有B中所有属性的对象的集合)。以后为了方便表示令f(X)=X*,g(B)=B*. 定义1.3[2]:设L(U,A,I)是概念格,其所有概念外延的集合记为LU(U,A,I)={X|(X,B)∈L(U,A,I)}.若对于两个概念格: L(U,A1,I1)和L(U,A2,I2),LU(U,A1,I1)=LU(U,A2,I2),则称L(U,A1,I1)与L(U,A2,I2)相等,记作L(U,A1,I1)=UL(U,A2,I2). 如果L(U,A1,I1)=UL(U,A2,I2),显然有L(U,A1,I1)艿L(U,A2,I2). 定义1.4[2]:对于形式背景(U,A,I),如果存在属性D哿A,使得L(U,D,ID)=UL(U,A,I),则称D是(U,A,I)的协调集。若进一步坌d∈D,L(U,D-{d},ID-{d})≠UL(U,A2,I2),则称D是(U,A,I)的约简。 所有(U,A,I)约简的交集称为(U,A,I)的核心。对于任何形式背景,其约简一定存在,但不一定唯一。 针对表1.1这个背景,概念格如下: (1,abde),(24,abc),(13,d),(124,ab),(U,覫),(覫,A)。相应的Hasse图为图1: 图1 背景(U,A,I)的概念格Fig1 The concept lattice of context(U,A,I) 定理1.1[2]:设(U,A,I)是形式背景,可将属性集A中的元素分为以下3种:绝对必要属性(核心属性)、相对必要属性和绝对不必要属性。其中,非核心中的属性称为不必要属性,它要么是相对必要属性,要么是绝对不必要属性。坌a∈A,记Ga={g|g∈A,g*劢a*}.下列命题成立: 由此我们可以找到形式背景的约简方法:首先根据上述定理对每一个属性进行判别,如果没有相对必要属性,则背景对应的核心属性就是唯一的约简;如果有相对必要属性,将其中属性值相同的分成一组,从每组相对必要属性中取一个属性与核心属性集取并集,这就是一个约简,由此所有组合就是全部约简。例如表1.1所示的背景中属性可有如下判别: 其背景的约简有两个:D1={a,c,d},D2={b,c,d}.c,d为绝对必要属性(核心属性),a,b为相对必要属性,e为绝对不要必要属性。形式背景(U,D1,ID1)的概念格如图2,显然它与图1所示的概念格同构。 图2 背景(U,D1,ID1)的概念格Fig2 The concept lattice of context(U,D1,ID1) 多光谱遥感影像处理一般是针对多波段光谱信息的联合处理,因此不但要考虑单个波段影像的统计特征,还要考虑波段间存在的相关性[7]。以下是常用的波段统计参量: 单波段图像(M×N)Aij(i=1,2,3…M;j=1,2,3…N),A0表示整幅图像的平均灰度值即: 标准差S定义为: 相关系数是描述波段影像间的相关程度的统计量,反映了两个波段影像包含信息的重叠程度。即 美国查维茨提出最佳指数OIF的概念,该方法可以给出n个波段组合中最优的指数大小,定义为: 此节讨论了基于概念格属性约简理论和离散化算法的多光谱遥感图像的波段约简的具体步骤。首先我们将每个波段作为一个属性列,每个像素对应为形式对象行,此时多光谱图像成为一个信息背景表,在此基础上通过阈值离散化将该信息表中的数值离散化为形式概念分析可以处理的0-1形式,最后按照第1节中的定理1.1的方法提取出核心属性(最佳波段)。该方法的优点是快速简单,与其他方法相比不仅节省了人力和时间,而且初步实现波段的优化组合。以下是流程框图: 图3 波段选择流程框图Fig3 The flow chart of wave band selection 本实验为了减少计算量,截取了一幅TM图像的250×200的范围进行实验验证。此实验图像的各个波段(1~6波段分别对应蓝波段、绿波段、红波段、近红外波段、红外波段和热红外波段)灰度图像如图4所示: 图4 TM图像的各波段原始影像Fig4 Original images of TM image 将6个波段的影像通过图像处理获取其灰度值,以每个波段为属性,然后形成形如表1.1的信息系统表,由于数据太多,并且图像左边有黑边,所以只从每个波段图像第30列截取其中20个数据显示如表4.1: 表4.1 原始TM遥感数据Tab4.1 The data of original TM image 由于表4.1内各个波段对应的值很繁杂,采用等间隔(阈值取110)的方法将其离散化,得到形式背景表4.2: 表4.2 形式背景Tab4.2 Formal context 根据定理1.1中的方法计算得出该背景的核心属性为 (Band1、Band5), 相对必要属性为(Band2、Band4、Band6),绝对不必要属性为(Band3)。 因此约简结果是波段{1,2,5}、波段{1,4,5}或波段{1,5,6}。但要综合考虑到波段影像所包含的信息量,参考表4.3表示的由第2节中提出标准差方法排列的波段信息量: 表4.3 波段标准差Tab4.3 standard dispersion of every band 由上表得知波段的信息量按大小排列为:Band5>Band3>Band2>Band1>Band4>Band6,由此得出最佳波段选择结果波段{1,2,5}。 实验结果分析:根据本文提出的方法得到的三个最佳波段组合可以通过第2节中提到的参量来验证其有效性。如表4.4和表4.5所示,波段组合的方式应按照下面顺序选择:{1,2,5}>{1,2,3}>{1,3,5}>{1,2,4}>…,而通过波段间相关系数比较,波段{1,2,5}优于波段{1,4,5}和波段{1,5,6}。通过综上所述,波段约简得出的结果是有效的。 表4.4 波段间相关系数Tab4.4 The correlation coefficient of bands 表4.5 波段组合的最佳指数Tab4.5 The OIF of bands 为了检验选择出的最佳波段用于分类中的效果,利用K-mean分类法对不同的图像分类,结果如图5所示,图5(a)为原始图像,图5(b)为本文方法选择出的最佳波段合成的伪彩色图像,5(c)为利用K-mean分类法对图5(b)分类后的效果图,图5(d)为对全波段影像即图(a)用K-mean分类后的效果图。对比两张效果图,我们不难发现,本文提出的最佳波段分类效果要好于使用全波段参与分类的效果,因此,我们不仅验证了在遥感影像处理中波段选择和数据降维的必要性,也证明了本文提出的波段选择方法是行之有效的。 (1)对于多光谱遥感影像,进行数据降维和波段选择是必要的,这样不仅可以缩短影像处理时间,减少计算量,而且很大程度上改善了光谱特征的应用效果。 (2)在多光谱遥感影像处理中引入形式概念分析的理论成果,应用属性约简的思想实现最优波段的组合选择是可行的,而且本文方法的计算时间只消耗在核心属性的提取上,相比其他方法节省了时间和人力。 (3)本文设计的波段选择方法只是利用概念格理论成果到遥感影像处理中的一个初步尝试,对于当前应用广泛的高光谱影像,由于其波段众多,本文方法的计算量就过于庞大,难于实现。在第4节中采用的阈值离散化方法中所选取的阈值110是通过人工干预选取的,并非机器学习后自动获取的,这个问题还有待进一步更好地解决。本文力图引进一种数据降维和最优波段组合的新方法,其相关应用还需进一步探索和开发。 [1]朱述龙,朱宝山,王红卫.遥感图像处理与应用[M].科学出[1]版社,2006(2). [2]张文修,魏玲,祁建军.概念格的属性约简理论与方法.中[1]国科学E辑信息科学.2005,35(6):628-639. [3]Ganter B,Wille R.Formal concept analysis: mathecal[1]foundations.New York:Springer Verlag,1999. [4]Wille R.Restructuring lattice theory:an approach based on[1]hierarchies of concepts.In:Rival I.(ed.)Ordered sets.Reidel:[1]Dordrecht-Boston,1982,445-470. [5]Godin R.Incremental concept formation algorithm based on[1]Galois(concept)lattices.Computational Intelligence,1995,11[1](2):246-247. [6]张文修,姚一豫,梁怡.粗糙集与概念格[M].西安交通大学[1]出版社,2006(7). [7]钱乐祥等.遥感数字影像处理与地理特征提取[M].科学出[1]版社,2004(7).


3 多光谱遥感影像波段统计参量
3.1 各波段影像标准差:
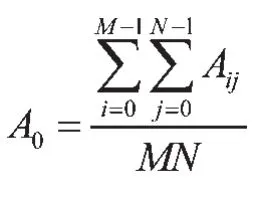

3.2 相关系数[7]:

3.3 最佳指数(Optimal Index Factor,OIF)[1]:

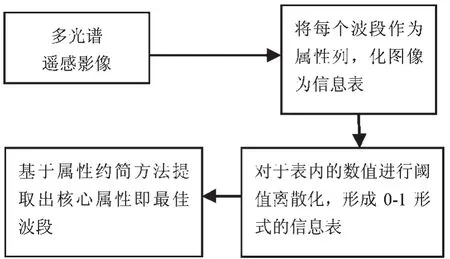
4 波段选择的流程设计及相关计算

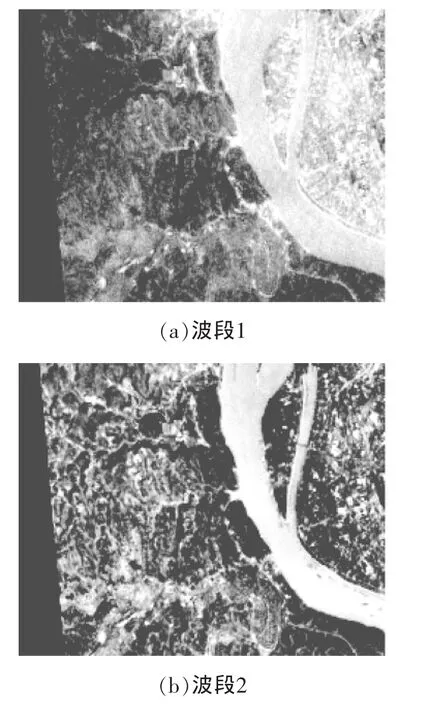
5 实验





6 结论

