基于互信息和自适应模板更新的目标跟踪算法

李 琼 ，王军宁

(西安电子科技大学通信工程学院，陕西西安 710071)

当前对图像序列进行目标跟踪的方法主要分为以下3种:基于运动分析的方法，基于状态滤波的方法和基于图像匹配的方法。其中，基于图像匹配的方法具有较强的抗遮挡、抗畸变能力，算法本身具有很强的鲁棒性。因此，被广泛应用于目标跟踪系统中。

灰度匹配是图像匹配中一类经典算法。在灰度匹配中，多采用模板图像与目标图像对应像素灰度差的累积和或者两幅图像的归一化度量来衡量两幅图像之间的相似性。灰度匹配算法常用的相似性度量有:互相关度量，如归一化互相关算法(NCC);距离度量，如差方和算法(SSD)、绝对差和算法(SAD、MAD)、最多近邻点距离算法(MCD)以及临近差方和算法(SSCD)。

基于归一化互信息的目标跟踪算法是一种基于对灰度统计值的图像匹配算法，它可以持续稳定地跟踪目标，并在目标发生刚体旋转和光照条件发生变化时仍然能够有效地跟踪目标[1]。但是，当目标发生较大的尺度变化时，该算法表现得不是很适应。结合这一问题，引入基于多尺度图像信息量的自适应模板尺寸更新策略，使算法在目标大小发生变化时能够实时并且合理地对模板尺寸进行更新。

1 基于归一化互信息的目标跟踪

1.1 互信息理论

熵是随机变量不确定度的度量，表达的是一个系统的复杂性或不确定性。系统A的熵定义为

两个系统的联合熵定义为

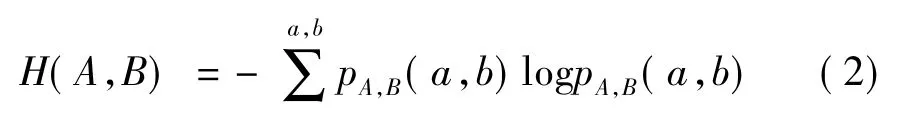
其中，a∈A，b∈B。这里，pA(a)为边缘概率密度函数，简记为p(a);pA，B(a，b)为联合概率密度函数，简记为p(a，b)，可用两图重叠部分的边缘灰度直方图和联合概率直方图来估计。

采用直方图的方法对联合概率密度进行估计，设h(a，b)表示随机变量A和B的二维联合直方图，则其联合概率密度p(a，b)的估计为

互信息 ( Mutual Information，MI)是信息理论中的一个基本概念，它是一个随机变量包含另一个随机变量信息量的度量。常用于描述两个系统间的统计相关性，可用熵来描述。

将两幅图像的灰度值看作两个随机变量A和B，其灰度值均为0～255，概率密度函数分别为p(a)和p(b)，则随机变量A和B的互信息可以表示为

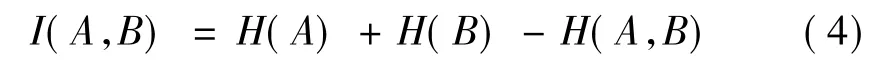
式中，H(A)、H(B)和H(A，B)为随机变量A与B的个体熵和联合熵。

根据式(1)～式(3)和式(4)，可推出互信息的计算式(5)，即为联合分布和乘积分布之间的相对熵

互信息量度量了两幅图像的统计独立程度。对于两幅图像而言，它是这两个随机变量统计相关性的测度，当两幅图像达到最佳匹配时，它们对应像素的灰度互信息达到最大值，由此可以确定图像的最佳匹配点。

1.2 归一化互信息

Studholme等人认为，互信息对重叠区域的变化非常敏感，在匹配过程中容易导致错误的结果，并给出了以下归一化的互信息(Normalized Mutual Information，NMI)

与之等价的一种方法是Maes等提出的熵相关系数(ECC)

由式(6)可知，归一化互信息是边缘熵和联合熵的比值，边缘熵的增加受联合熵增加的约束。当两幅图像匹配不准时，边缘熵增大，联合熵也会增大，归一化互信息量就不是最大;随着匹配准确度的提高，图像的联合熵取值逐渐减小，归一化互信息量随之增大。归一化互信息的最大化就是使边缘熵相对于联合熵最大。归一化互信息，一方面考虑了匹配时联合熵较小，另一方面考虑了重叠区域内图像的信息，同时又较好地平衡了两者之间的关系。实践证明，该方法比最大互信息法的匹配精度更高、稳定性更好。采用式(7)的互信息归一化模型，当两幅图像完全匹配时，互信息取最大值1。

1.3 基于归一化互信息的图像匹配

基于互信息的图像匹配算法具有匹配精度高、抗遮挡和抗光照变化等优点。其实现的具体步骤是:在目标图像中为每个搜索点分割一个与模板同样大小的图像，计算它们的互信息值;得到一个互信息的曲面，曲面中最大值对应的点即为模板图像在目标图像中的最佳匹配位置。

为验证基于归一化互信息的图像匹配算法，这里以82×97像素的模板在512×384像素的目标图像中进行匹配，如图1所示，图1(a)为模板图像，图1(b)为待匹配图像，图1(c)为匹配结果，图1(d)为归一化互信息匹配的相似度曲面，曲面的最大值即为最佳匹配点，归一化互信息值为1。

图1 互信息匹配结果及其模板

1.4 基于归一化互信息的目标跟踪

为验证基于归一化互信息(NMI)的目标跟踪算法的适应性，通过几组实验，证实该算法具有以下几个优点:

(1)在目标旋转和光照条件发生变化时仍然能够有效跟踪目标[1]。

归一化互相关算法(NCC)本身对图像的亮度变化和对比度变化不敏感，当被跟踪目标图像的光照条件发生变化时，其具有一定的鲁棒性;但当光照条件发生剧烈变化时，它便因难以适应而可能导致匹配失效。基于归一化互信息方法，能够保证在光照条件发生剧烈变化或者图像对比度发生明显变化时，仍然匹配正确，从而提高了跟踪的可靠性。

图2中，分别用同一个模板去匹配光照发生剧烈变化，目标与背景灰度非常接近的原图。圆点为匹配中心，矩形框为模板边缘。由图可知，图2(a)匹配效果很好，图2(b)匹配失效。可见，归一化互信息算法在抗光照方面，较归一化互相关算法具有更强的鲁棒性。

图2 光照变化情况下的匹配结果对比图

(2)在目标变形或者被遮挡时具有一定的抵抗能力。

图3中，利用归一化互信息跟踪算法跟踪飞机起飞、前进和下降的整个过程。在这个过程中，飞机从背景简单区域开始，中途经历了被背景半遮挡和完全遮挡，最后又飞回到背景简单区域。第260帧中，飞机与树木的灰度很相近，目标被准确跟踪;第285帧、287帧中目标被部分遮挡，第286帧中目标被完全遮挡，但到第288帧目标仍然被准确跟踪。由此可见该算法具有一定的抗遮挡性。

图3 目标遮挡情况下的跟踪结果图

去均值归一化相关算法是对NCC的一种改进形式，它利用去均值的结果来衡量相似度，实现方便且精度较准，一定程度上克服了NCC在某些情形下检测不到准确尖峰位置的缺点。因此在抗光照方面，与文中提出的NMI算法具有同等的鲁棒性，但在抗遮挡方面就不及NMI了。

(3)在目标轮廓模糊和低对比度时能保证较好的匹配精度和较高的稳定度。

图4中，利用归一化互信息跟踪算法跟踪对比度很低，轮廓非常模糊的卡车行驶序列图。在行驶过程中，卡车伴随有转弯等运动，且目标渐渐变小。为更好地表征结果，在该实验中，每隔24帧对模板进行固定比例的缩小。从图3可以看出，归一化互信息跟踪算法在轮廓非常模糊，对比度很低的情况下也能保证跟踪的有效性。

图4 低对比度情况下跟踪结果图

(4)互信息度量中包含了图像的边缘和纹理等信息，因此无需提取图像边缘和纹理等特征，可以直接对实时图像进行匹配跟踪，从而节省了算法的执行时间。

2 基于多尺度图像信息量的模板尺寸更新

2.1 自适应模板更新算法

运动目标的外观在跟踪过程中是不断变化的。尺寸固定不变的模板图像，很难有效跟踪尺寸实时变化的目标图像。针对这一问题，在归一化互信息匹配的基础上，将多尺度图像的信息量度量方法引入目标跟踪中，根据信息量的变化自适应更新模板尺寸的大小。

尺度空间中图像的信息量由图像中两类特征点的数量来度量。从微分算子的局部极值角度统一这两类特征点。假设在2维图像平面内，点P为图像f(x，y)内某像素点，1～8为点P的8邻接像素点N8(P)。现以P为极点，建立极坐标系，设极角为l，l∈L，L={kπ/4，k=-4，…，0，…，3，k∈Z}，则对P的8邻接像素点进行如下的数学描述[6]

在极角l方向上，取步长Δh=1，定义f(x，y)的方向微分算子

文献[5]中两类特征点的定义如下:

定义1设2维离散平面上点P(x，y)，若∀l1，l2∈L，L={kπ/4，k=-4，…，0，…，3，k∈Z}，当l1-l2=mπ，m=±1时，Δl1f(x，y)·Δl2f(x，y)＞0，则点P称为第1类特征点。

定义2设2维离散平面上点P(x，y)，若∀l1，l2∈L，L={kπ/4，k=-4，…，0，…，3，k∈Z}，当l1-l2=mπ，m=±1时，Δl1(fl1(x，y)-fl2(x，y))·Δl2(fl1(x，y)-fl2(x，y))＞0，则点P称为第2类特征点。

图像信息量定义为两类特征点的和。当物体尺寸由小变大时，其图像信息量的值也由小变大[6]。根据文献[6]给出的图像信息量的比值和物体尺寸之间的关系，文中关于模板尺寸更新算法的主要思想是:给定一个阈值Th≤1，如果用归一化互信息算法跟踪目标，当归一化互信息值ECC＜Th时，则说明目标跟踪精度不在可接受的范围内，此时就需要根据信息量的变化对模板尺寸进行更新。

计算第1帧图像中模板的初始化图像信息量E1和第1帧图像中对模板尺寸乘以1±α(0≤α≤0.5)后的区域信息量E2，E3，类似地，在需要更新模板尺寸的当前帧，计算的信息量分别为E4，E5，E6;为后续帧的模板更新做准备，根据新模板尺寸计算当前帧中模板图像信息量E1，E2，E3，由以上步骤类推后续帧中模板尺寸更新过程;并设尺寸变化比例为Zoom。

假如满足E5＞E2，判断目标尺度可能增加，按公式(10)计算尺寸变化比例Zoom;否则，目标尺寸可能减小，按照式(11)计算Zoom。

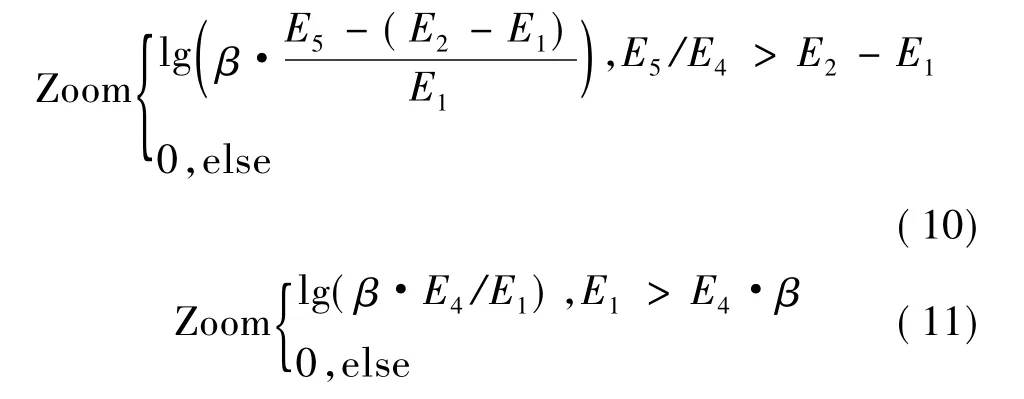
式中，参数β用来消除背景对目标信息量的影响，其值接近1;当背景越复杂时，β值与1的差值越大;当目标尺寸增大时，β≥1;反之，β≤1。由计算得到当前帧的尺寸变化比例Zoom后，即可得到模板的高度和宽度需更新的比例(1+Zoom)。最后按照计算得出的比例对模板图像进行放大或缩小。在模板放大或缩小过程中，采用3次卷积插值法处理变化后的图像。这样得到的更新后的模板图像，轮廓清晰，质量较高。

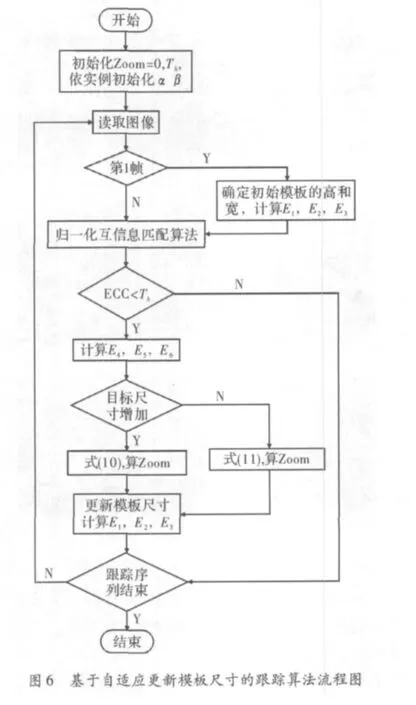
图5是模板更新前后的对比图，更新前像素为82×97，更新后像素为77×91。从图5可以看出，更新后的模板图像并未出现模糊和细节不清楚的现象，可见，3次卷积插值法能够较好地保持图像的边缘细节。图6是基于图像信息量的自适应更新模板尺寸的跟踪算法流程图。

2.2 实验结果与讨论

结合提出的模板尺寸自适应更新策略，采用基于归一化互信息的目标跟踪算法，在Matlab环境下对几组图像序列进行实时跟踪。

实验一跟踪目标逐渐变小的卡车行驶序列图。其中，图像尺寸为384×512，搜索区域尺寸为20×20。图7是跟踪结果，图中矩形框表示模板边界;圆点表示模板中心，即跟踪的最佳位置。模板尺寸随着目标的变化而变化，而且尺寸更新效果很好。

图7 目标渐下的跟踪结果

实验二跟踪迎面驶来的小汽车序列图。在这个序列图中，目标逐渐变大，且每帧之间尺寸变化很明显。图像尺寸为385×289，搜索区域尺寸为15×15。图8是跟踪结果。跟踪过程中模板尺寸随着目标的变大而变大，在第111帧，目标几乎充斥了整个画面，效果依然很好。

图8 目标渐大的跟踪结果

实验表明，基于多尺度图像信息量的模板尺寸更新算法可以适时准确地更新模板。

3 结束语

介绍了一种基于归一化互信息的跟踪算法，该算法与其他相关匹配算法相比，具有较强的鲁棒性，如在光照变化的情况下，仍能实现正确的图像匹配;在目标遮挡和低对比度情况下，能够实现精确的目标跟踪，对环境变化具有较强的适应性。在此基础上，又引入了基于多尺度图像信息量的自适应模板尺寸更新算法。该算法利用图像匹配得到的互信息值作为阈值，计算尺度空间中图像的信息量，模板尺寸根据计算的信息量大小进行自适应调整，从而较好地适应了跟踪目标大小的变化。实验表明，加入模板尺寸自适应更新算法后，跟踪性能进一步增强，跟踪效果进一步改善。进一步的研究方向是模板尺寸更新算法中更新阈值Th的自适应性。

[1]惠斌，陈法领，罗海波.基于互信息的目标跟踪方法[J].红外与激光工程，2007，36(7):209-212.

[2]周友兵.基于归一化互信息的CT-MRI脑图像配准[J].现代电子技术，2007(8):101-102.

[3]付梦印，刘羿彤.基于互信息测度红外目标图像相关匹配跟踪算法[J].兵工学报，2009，30(3):371-374.

[4]THOMAS M COVER，JOY A THOMAS.Elements of Information Theory[M].北京:清华大学出版社，2002.

[5]王郑耀，程正兴，汤少杰，等.基于视觉特征的尺度空间信息量度量[J].中国图象图形学报，2005，10(7):922-928.

[6]钱惠敏，茅耀斌，王执铨，等.自动选择跟踪窗尺度的Mean-Shift算法[J].中国图象图形学报，2007，12(2):245-249.

[7]贾桂敏，王向军，张世海.复杂背景下基于自适应模板更新的目标跟踪算法[J].光学学报，2009(3):659-663.