一种道岔外锁零件疲劳寿命的分析方法

龚海飞 孙晓勇 王亲敏 高 岩

（中国铁路通信信号集团基础设备事业部，北京 100166）

1 概述

工程结构或机械零部件，总是在某种载荷的作用下工作。机械零部件的载荷通常分为静载荷和动载荷两大类，静载荷是指相对稳定不变的载荷，而动载荷是按照一定规律变化或随机变化的载荷。在动载荷的循环作用下，材料、零件或结构发生失效称为疲劳。从破坏机理上看，疲劳失效与静载荷破坏有着本质的区别。静载荷破坏通常伴有明显的塑性变形，在静应力小于屈服极限时，一般不会发生。疲劳破坏发生在疲劳应力小于屈服极限时，并且失效时不会出现宏观的塑性变形（即使是塑性好的金属材料），事先不易觉察，通常类似于脆性断裂突然发生，具有更大的隐蔽性和危险性[1]。在铁路道岔中，外锁零件长期工作在行车引起的冲击动载荷中，零件容易产生疲劳损伤[2]，因而，分析和确定外锁零件的安全有效期限即疲劳寿命有着重要的意义。

一般而言，分析和确定零件的疲劳寿命有理论建模[3-5]、试验测试[6-8]和手册查找[9-11]等方法。理论建模充分利用现代化的计算手段，建立受力模型，结合疲劳分析理论来计算疲劳寿命，这种方法成本低、效率高，但分析误差偏大；试验测试利用分析对象的实物，模拟分析对象承受的载荷，通过大量的试验得到疲劳寿命数据，这种方法精确度高，但费时费力，成本高；手册查找主要是利用手册中现有的结论或数据，得到分析对象的强度极限和疲劳极限，来评估零件的疲劳寿命，是一种近似类推的方法，简便、易操作，但误差偏大。道岔零件工作在风沙多尘的露天复杂环境，单一的疲劳寿命分析方法，很难满足道岔零件疲劳寿命分析的需要。在道岔实际工程分析和设计中，提出一种操作性强、分析效率高以及成本和精度相对适中的疲劳寿命分析方法，显得十分必要。

本文针对铁路道岔外锁零件的实际工况，探讨一种疲劳寿命分析的简便方法。结合理论分析计算和疲劳手册数据，利用现场测试结果建立道岔零件疲劳寿命的分析方法，充分利用理论分析、现场测试和手册数据三者的优势，方便高效地评估道岔零件的疲劳寿命。

2 分析方法

2.1 薄弱位置

选取客专18号道岔中，受力较大的心轨第二牵引点关键零件锁钩为对象，进行实例分析。锁钩的基本结构参数为长887 mm，高86 mm，最小加工圆角R8，使用材料为45#钢调质，表面粗糙度Ra为25m，材料弹性模量E为210 GPa。对于常用的45#钢调质，拉伸强度极限σb和屈服极限σs分别为705 MPa和450 MPa[12]。行车时，锁钩的受力可以简化为如图1所示的力学模型。图1中，锁钩受到心轨侧翻趋势产生的水平挤压和向下的摩擦作用，导致锁钩同时承受水平和竖直方向的疲劳载荷。由于竖直方向的载荷是锁钩与心轨在水平挤压的作用下产生的摩擦力，依据钢材通用的滑动摩擦系数范围0.01～0.5[13]，按工程经验取摩擦系数为0.2，那么竖直载荷可以由水平载荷按照摩擦系数折算得到。在实际工作中，锁钩与锁闭杆、锁闭铁的约束均为受力接触。为了简化计算，考虑把锁闭铁作为固定约束，而锁闭杆的约束仍为受力接触。与锁闭杆直接接触的锁闭框和转辙机连接销，没有与锁钩直接相连，在锁钩的受力分析中均作为固定约束。

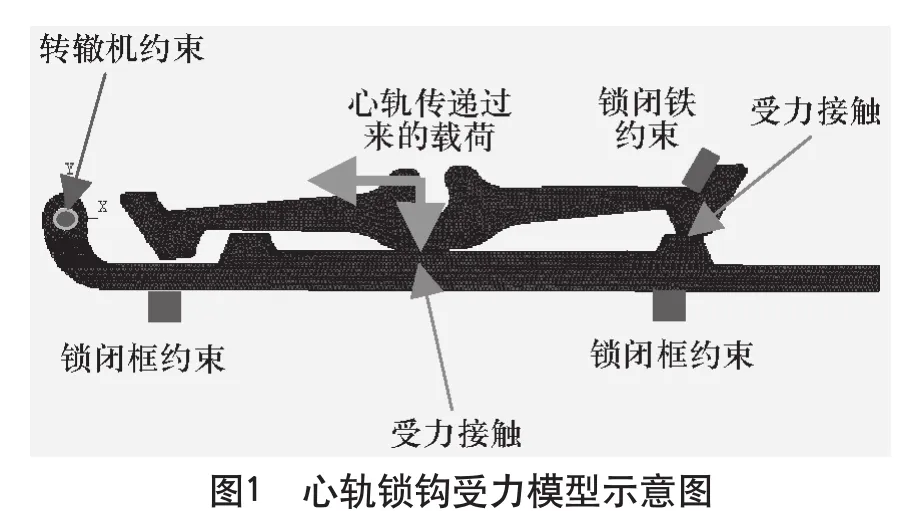
图2为锁钩结构强度薄弱部位的分析结果。结构强度中，Mises综合应力较大的部位为零件的薄弱部位，是容易出现疲劳损伤的位置[14]。从分析结果上看，锁钩有3个相对薄弱的部位，分别位于锁钩中部安放心轨的圆槽底部、与锁闭铁接触的锁钩尾部以及与锁闭杆接触的锁钩底部。这3个薄弱位置中，理论上他们发生疲劳失效的可能性均比较大，而且均早于其他部位，然而第一个薄弱部位的应力最大，在水平载荷1.5 t、竖直载荷0.3 t的条件下，其Mises综合应力最大已达到80.09 MPa，我们选取薄弱部位1进行后续的分析。

2.2 疲劳S-N曲线

为了评价零部件的疲劳寿命或疲劳强度，需要建立外加应力S与疲劳寿命N之间的关系，即S-N函数模型。工程上，一般以疲劳应力幅值作为S，循环破坏次数作为N，作S-N曲线。描述这种S-N曲线关系的模型主要有5种[15]。这5种模型具有各自的特点和适用范围。工程上一般采用经典的幂函数模型Sa·N=C（a和C为常数）来描述零件的疲劳S-N关系。锁钩材料为45#钢，其S-N曲线数据可以由文献[9]查得。文献中，有疲劳可靠性50％至99.9％的多种S-N曲线，选取可靠性较高的99.9％的S-N曲线提取分析数据。采用幂函数模型Sa·N=C的双对数坐标表示疲劳S-N曲线。通过曲线拟合计算，得到模型的常数a和C，代入幂函数模型，得到锁钩的S-N曲线对数坐标形式如（1）式所示。

幂函数疲劳模型Sa·N=C，即LgN=a+b·lg S中，常数a和C的大小分别为1045.95684和15.647 72，那么锁钩的疲劳寿命模型如（2）式所示。

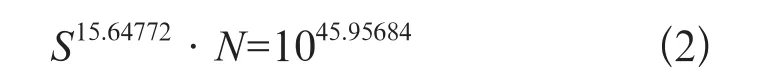
2.3 应力换算和疲劳寿命

如图3（a）所示，为列车通过时锁钩测试位置的现场实测波形。从图中可以看出，行车时锁钩承受以脉冲为主要特征的冲击载荷。通常，手册上查得的S-N曲线数据是按照对称循环应力进行旋转弯曲疲劳试验，得到的数据结果。当工况中的应力循环特征与S-N曲线模型中的加载循环特征不同时，按照前面的分析，我们采用古德曼（Goodman）方程[15]进行应力换算，采用换算后的应力值进行疲劳寿命计算。

对图3（a）所示的现场测试结果进行信号分析处理，去除信号斜坡和直流成分，得到如图3（b）所示的锁钩疲劳冲击测试分析波形。对图中所示的冲击波形应变幅值进行简单平均处理，得到表1所示的锁钩应力应变测试结果。表1中，通过一趟列车产生的16个主要脉冲的平均应力峰值为1.869 MPa，平均应力谷值为1.197 MPa，那么平均应力幅值为1.533 MPa。根据现场测试得到的应力结果，锁钩工作时疲劳循环应力远低于其屈服强度450 MPa，锁钩的应力与应变关系在线弹性变化范围内[16]，可以从锁钩测试部位的实测应力折算到薄弱位置的工作应力，即锁钩工作时薄弱部位的实际疲劳应力。如图4（a）所示，在同一载荷下，锁钩测试部位的主应力为5.027 MPa，薄弱部位的主应力为99.350 MPa，那么锁钩薄弱部位主应力是测试部位主应力的99.350/5.027倍。测试部位在行车时其疲劳冲击平均主应力幅值为1.533 MPa，那么锁钩薄弱部位的主应力幅值大小为 99.350/5.027×1.533等 于 30.297 MPa。根 据第四强度理论，采用Mises综合应力来评价锁钩薄弱部位的疲劳强度。根据图4（b），对比薄弱部位的主应力和Mises综合应力的大小，可以得到锁钩薄弱部位的Mises综合应力的应力幅值σma为80.09/99.350×30.297等于24.424 MPa。

考虑到行车现场应力循环特征类型与疲劳实验加载循环特征的不同，按照古德曼方程进行应力换算，换算后循环应力幅值σma为25.301 MPa。由公式（2），行车时一次冲击对锁钩造成的疲劳损伤D为 [（KσS）15.64772]/（1045.95684）等于 2.546 3×10-22，Kσ为锁钩薄弱部位的应力集中系数，详见下一节。由测试波形看，通过一列火车对锁钩产生16次疲劳冲击，那么通过一趟火车对锁钩的冲击疲劳损伤Dsum为16×D等于4.074 2×10-21，那么，锁钩的疲劳寿命N为1/Dsum等于通过2.454 5×1020趟火车。

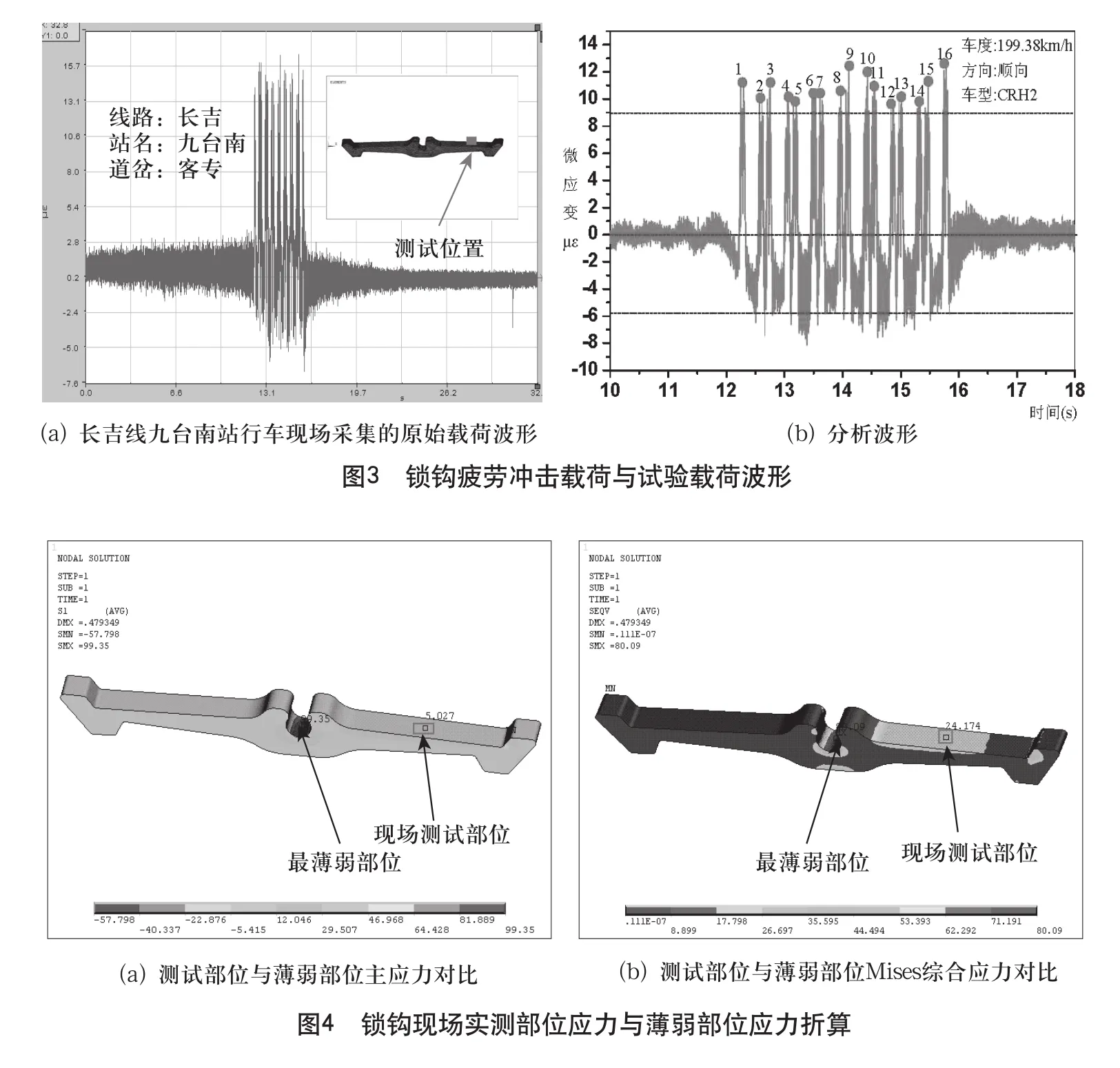
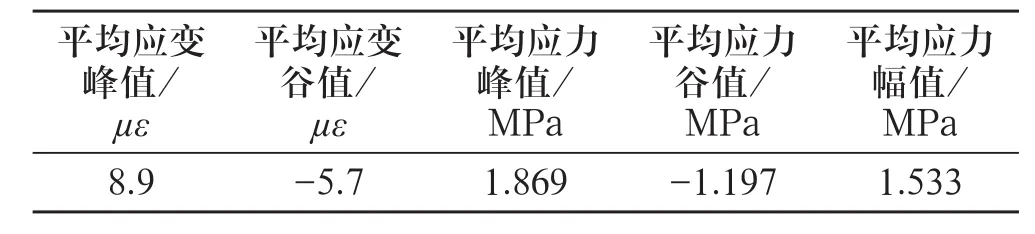
表1 长吉线九台南站心轨二动锁钩应力现场实测结果

2.4 结构及环境因素

在实际工程中，除了冲击载荷的作用，零件自身的结构，如过渡圆角、沟槽和表面状态等，以及零件所处的工作环境，如温度、腐蚀和磨损等，都不同程度地影响着零件的疲劳寿命。锁钩工作在风沙多尘的露天环境，并且锁钩尺寸大小与疲劳试验样品的尺寸不同，采用结构尺寸系数和环境影响系数，来修正锁钩的疲劳寿命。

零件结构引起的应力集中对疲劳的影响，由应力集中系数来界定。应力集中系数Kσ为1+qσ（ασ-1），其中，qσ为应力集中的敏性系数，它与零件的材料强度极限和应力集中部位的圆角半径相关；ασ为应力集中结构系数，它与应力集中部位的结构形式和尺寸大小有关。应力集中系数可以由计算或查手册得到。

试验测定疲劳S-N曲线时，一般采用7～25 mm的标准试样进行试验，而实际中使用的零件尺寸与试样尺寸存在不同程度的区别。随着零件尺寸的增大，零件表面发生缺陷的可能性也随之增大，疲劳强度和疲劳寿命相应降低。采用尺寸效应系数来修正由于尺寸大小不同引起的疲劳寿命偏差。尺寸效应系数用εσ表示，根据零件材料及尺寸大小，可以在相关的疲劳手册中查得。

通常，零件的最大应力和疲劳源出现在零件的表层或次表层，表面加工的刀痕、擦伤和氧化等将引起表面应力集中，降低疲劳寿命[17]。表面状态对疲劳的影响通过表面质量系数β来表示。常见的加工方式及其表面质量系数，可以在机械相关的材料设计手册中查得。腐蚀环境的腐蚀方式和腐蚀介质对疲劳寿命的综合影响用γ来表示。常用材料的γ也能在机械设计手册中查得。研究和工程实践表明，对于碳钢和合金钢，当环境温度达到200 ℃以上高温时，温度对疲劳寿命有明显的影响[18]。由于道岔工作的环境温度在100 ℃以内，这个范围内的温度对碳钢的影响很小，可以忽略不计。另外，已有研究表明，疲劳冲击的频率对疲劳寿命的影响很小，在此也忽略不计。由于道岔外锁零件工作环境恶劣，在考虑这些影响因素的取值时，采用保守原则，典型结果如表2所示。

表2 道岔零件疲劳寿命影响因素

修正后，锁钩的疲劳寿命N为εσ·β·γ·N等于4.639 0×1019趟火车，单次分析计算的可靠性由S-N曲线的可靠性决定，为99.9％。理论上，金属零件的疲劳寿命超过107，就可以认为是无限寿命。另外，可以通过大量的不同行车现场的测试结果，以及零件的不同部位来计算疲劳寿命，然后进行科学统计分析，提高疲劳寿命计算的可靠性和准确性。

3 结论与展望

道岔外锁零件工作环境恶劣，影响疲劳寿命的因素复杂，采用理论分析、手册资料和现场测试三者有机结合的方法，评价道岔零件的疲劳寿命是切实可行的。这种方法操作简便，针对性强，精度适中，为道岔零件的设计、维护和优化提供技术参考。在工程上，对于某些非常重要的零件或零件的关键部位，可以通过不同行车现场采集的疲劳载荷以及同一零件不同的薄弱部位，分析计算大量的疲劳寿命结果，通过科学统计来全面评价道岔零件的疲劳寿命。

4 致谢

感谢中国铁路通信信号集团基础设备事业部测试组和结构设计组，在现场测试和受力分析方面的支持和帮助。

[1]曾春华，邹十践.疲劳分析方法及应用[M].北京：国防工业出版社，1991.

[2]蔡小培.高速道岔尖轨与心轨转换及控制研究[D].成都：西南交通大学，2008.

[3]吴富强，姚卫星.一个新的材料疲劳寿命曲线模型[J].中国机械工程，2008，19（13）：1634-1637.

[4]王国军，闫清东.齿轮弯曲疲劳寿命有限元计算方法研究[J].农业装备与车辆工程，2008（1）：40-42.

[5]郭祖华，平安，王德俊.结构疲劳寿命估算的计算机仿真

[J].东北大学学报（自然科学版），1998，19（3）：302-305.

[6]赵隆威，毛增滇，胡善荣，等.CS931型10吨载重半挂车应力测定应力分析及疲劳寿命估算[J].试验力学，1986，1（4）：322-330.

[7]鄢奉林，陆兵，倪利勇.钢制车轮动态弯曲试验疲劳寿命预测[J].机械设计与制造，2010（6）：117-119.

[8]黄学伟，蔡力勋.薄片漏斗试样的应变等效换算与Zr-4合金疲劳寿命估算[J].实验室研究与探索，2007，26（11）：180-184.

[9]中国航空材料手册编辑委员会.中国航空材料手册[M].北京：中国标准出版社，1988.

[10]高镇同.疲劳应用统计学[M].北京：国防工业出版社，1986.

[11] TB/T1335—1996 铁道车辆强度设计及试验鉴定规范[S].北京：中国铁道出版社，1996.

[12]中国第一汽车集团公司编写组.机械工程材料手册（金属材料）[M]，北京：机械工业出版社，1998，12.

[13]温诗铸，黄平.摩擦学原理[M].3版.北京：清华大学出版社，2008.

[14] Zefeng WEN, Xuesong JIN，Weihua ZHANG.Contact-Impact Stress Analysis of Rail Joint Region using the Dynamic Finite Element Method[J].Wear，2005，258 ：1301-1309.

[15]姚卫星.结构疲劳寿命分析[M].北京：国防工业出版社，2003.

[16]吴家龙.弹性力学[M].北京：高等教育出版社，2008.

[17] BAYRAKTAR E，MORA R，GARCIA I M，et al.Heat treatment，surface roughness and corrosion effects on the damage mechanism of mechanical components in the very high cycle fatigue regime [J].International Journal of Fatigue，2009，31（9）：1532-1540.

[18]机械设计手册编委会.机械设计手册（第5分册）[M].北京：机械工业出版社，2006.