属性数学在铁路交通安全综合评价中的应用
宁 静 ,佘振国,蒋 荟
(中国铁道科学研究院 电 子计算技术研究所,北京 1 00081)
我国铁路建设正处在快速发展的重要时期,铁路运输安全面临着巨大挑战。长期以来,我国铁路安全监察部门普遍采用单一的反馈控制安全管理模式,已不能适应铁路快速发展和现代铁路运输安全监察管理工作的需求。铁路运输安全生产的重要内容之一是对运输生产系统进行综合的安全预警分析、安全评估,并采取对策、措施来控制、消除其中的各种安全隐患,预防事故及危害的发生,从而实现铁路安全运输。由于铁路运输涉及多种专业、设备更新快,受外部环境、气候条件等不可控制因素制约等特点,其安全工作效果的评价与衡量尚未形成一个比较科学的评价体系。作为事前预防进一步落实问题的有效手段,为了企业落实安全生产责任和铁路运输安全生产行业的管理提供理论依据,急需建立铁路运输安全生产安全综合评价体系。
铁路交通安全监督管理信息系统(以下简称安监信息系统)的建设和应用,主要服务于铁路安全监察部门,接入了铁道部和铁路局在运用和管理上相对成熟的监测系统信息,共享有专业安全管理和事故调查处理分析等信息,实现部、局、站段3级应用,通过对信息的分析、预警、分类掌握、分级管理和综合应用,实现了监测报警、安全检查、事故调查和安全综合分析4个方面的闭环管理,为铁路交通安全管理的有序可控提供强有力的技术支撑。同时,该系统收集的设备监测报警、安全检查和事故调查处理信息为安全评价和安全管理提供了数据支持。
本文构建了铁路交通安全综合评价指标体系,提出基于属性数学的铁路交通安全评价方法,并使用安监信息系统采集的信息,验证了评价模型的可行性。
1 铁路交通安全综合评价的关键问题
1.1 安全评价指标体系的建立
评价指标体系的选择和确定是进行安全综合评价的基础和关键,直接影响到评价的精度和结果。通过对铁路运输安全生产和管理的实际情况分析,结合目前铁路安全管理和灾害预警管理[1~3]的评价考核指标,建立了铁路交通安全综合评价指标体系。
设备监测报警、安全检查和事故调查处理信息为各级安全监察部门进行铁路安全运输生产的监督管理提供了有力的支持,这些数据符合所建立评价指标体系的要求,也验证了其合理性和可行性。本文建立的3层评价指标体系如图1。

图1 铁路运输安全评价指标体系
1.2 权重的关联度评价
可用的,否则认为权重不可用,需要调整,并给出指标关联度排序,为合理调整权重提供理论依据。
灰色关联度算法如下[4]:
指定参考序列,表示为x0(k)。被比较序列,表示为xi(k),i=1,2…m
当某一比较序列作为参考序列时,两比较序列绝对差:

△ij(k)为xi和xj之间第k个差的绝对值,xi为参考序列、xj为其它比较序列。
(1)求得所有比较序列在各点的绝对差中最小值与最大值:

(2)计算灰关联系数r(xi(k), xj(k)):

其中i=1,2,3,…,m, j=1,2,3,…n, j∈i,最大差△max、最小差△min及辨识系数ζ。辨识系数ζ∈[0,1],大小可以根据实际需要作适当调整,由实际的数学证明中可知,其大小只会改变相对数值的大小,不会影响灰关联度的排序,一般ζ取值为0.5。
(3)计算灰关联度r(xi, xj):
当求得灰关联系数后,取灰关联系数的平均值作为灰关联度:

1.3 属性数学评价模型描述
1.3.1 属性集与属性测度
属性数学的立足点是属性集与属性测度[5],现通过例子解释这2个概念。设x为评价的对象,x中元素的某类性质,即记为F称为属性空间。例如,要研究某单位的安全工作状况,可以令F={安全评价成绩}。属性空间F中的任何一种状态,都称为一个属性集。例如,A={优秀}、B={良好}、C={合格}、D={不合格},A、B、C、D都是属性空间F={安全评价成绩}的一种状态,所以A、B、C、D都是属性集,都可看成F的子集。
用“x∈A”表示“x具有A属性”。用μx(A)定量地形容“x具有A属性”的程度,称它为x∈A的属性测度。为方便起见,要求属性测度在[0~1]之间取值。不同的属性集都可以有相应的属性测度,而这些属性测度必须满足一定的规则[5~6]。

1.3.2 基于属性数学的安全评价模型
铁路运输安全评价属性数学模型的输入为第3层指标的测量值,即评价指标的实际测量值,模型的输出为评价类,即对该评价对象属于哪一类安全等级的判别或预测。根据属性数学模型,第3层单个指标的属性测度,按照指标值的大小和评价类的关系确定性能函数,根据测量值计算出性能函数值;最终评价结果及第2层和第1层指标的属性测度,由其下一层单个指标属性测度经加权求和得到的。最终评价结果,根据属性判别准则,确定该评价对象属于哪一个评价类。
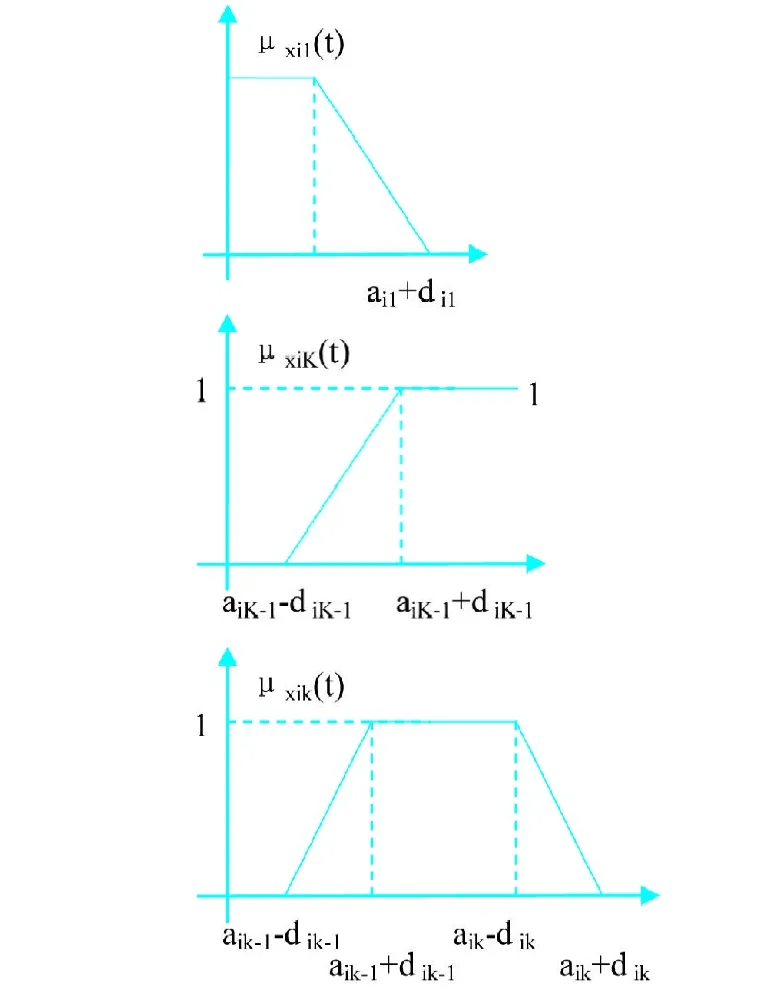
对于第3层单个指标的属性测度[7~8],设第i个指标的测量值为t,由图2所示的函数μxik(t)计算其属性测度。其中(aik-1, aik)为第i个指标第k类(等级)的划分标准,且ai0 图2 第3层单个指标的属性测度函数 得到最终评价的属性测度μx(k),1≤k≤K,再根据属性判别准则确定其评价集,即评价等级,本文采用置信度准则作为属性判别准则。设{C1,C2,…,CK}为有序分割,C1>C2>…CK, λ为置信度,通常要求0.5<λ≤1。 则认为评价对象属于Ck类。上述准则是要求“强”的类占相当大的比例。置信度λ一般取在0.6~0.7之间[5]。 将铁路运输的安全等级,即属性集或称评价集分为4类,评价集{C1,C2, C3,C4}={“优秀”,“良好”,“合格”,“不合格”},且C1>C2> C3>C4,是属性空间F的有序分割。上述图1,按照3层的指标体系对某单位的安全生产状况进行评价。 在灰色关联评判模型中,参考列是各指标的初始权重。以某路局最近3年各类事故的历史数据记录为依据,经分析整理,将事故样本划分到各指标,得到各指标的事故件数,作为灰色关联评价的被比较列。若被比较列与参考列的灰色关联度大小在可接受范围内,则说明用初始权重基本符合实际情况,反之,则要修改权重,并且使权重大小排序符合关联度的排序。根据最近3年事故样本计算的2组指标的关联度,如表1和表2。 表1 第1组指标关联度计算结果 表2 第2组指标关联度计算结果 表1中,所得的关联度均大于辨识系数ζ=0.5,因此,这组指标的权重可用。表2中,由于有一个关联度小于辨识系数,所以这组指标的权重不符合实际,需要调整。试验表明:利用事故样本计算各指标的关联度比,并参考指标关联度排序调整指标权重后所得的关联度均大于辨识系数,权重得以可用。试验结果见表3和表4。 表3 各指标关联度计算结果 表4 第2组指标权重调整后关联度计算结果 将设备监测和人工检查的安全信息经过加工,作为各指标的实测值。进行归一化处理,按照单个指标属性测度公式,计算单个指标属性测度,可构造第3层指标属性测度矩阵。表5是评价该路局某一月一组3级指标的属性测度。 表53 级指标属性测度计算结果 通过加权求和计算第2层、第1层指标属性测度矩阵,最终得出综合评价属性测度。计算结果见表6和表7。 表62 级指标测度计算结果 根据属性识别准则,判别出该路局属于“合格”级别。该评价结果与实际安全管理的定性分析结果相符。 表71 级指标测度计算结果 本文以研究铁路运输安全评价方法为出发点,通过对铁路运输安全生产系统和管理情况的分析,提出铁路安全评价3层指标体系,使安全评价更具规范性和可操作性。利用铁路交通事故与检查监测的安全问题之间的内在联系,用灰色关联分析法评判指标权重的合理性,给出调整权重的有效方法。最后采用属性数学综合评价法对某路局的安全生产状况进行评价,很好地解决了具有多个指标或属性的综合评价问题,使评价结果更加真实合理。利用某路局安监信息系统提供的数据对以上模型进行验证,结果表明,本文提出的评价模型可行和适用,是铁路运输安全综合评价的一种有效的方法。 [1]佘 廉,李 睿,李红九. 铁路运输灾害预警管理[M]. 河北:河北科学技术出版社,2004. [2]李培煊,岳 鹏,张毓贤,王剑平. 铁路运输安全考核指标体系与综合考核方法的探讨[J]. 铁道学报,1996. [3]王 超. 交通灾害中的载运工具致灾机理及其预警管理系统研究[D]. 武汉:武汉理工大学,2002. [4]赵勇钢. 铁路车站货运作业安全评价及管理的相关研究[D].北京:北京交通大学,2007. [5]程乾生. 属性集和属性综合评价系统[J]. 系统工程理论与实践,1997. [6]程乾生. 属性识别理论模型及其应用[J]. 北京大学学报(自然科学版),1997. [7]宋祥波. 基于属性数学的铁路线路安全评价方法的研究与应用[D]. 北京:北京交通大学,2006. [8]马 超. 基于未确知测度理论矿井通风系统安全评价研究[D]. 西安:西安科技大学,2005.

2 铁路交通安全综合评价应用实例
2.1 权重关联度评价




2.2 计算单个指标属性测度

2.3 计算最终评价测度和评价结果


3 结束语

