基于FFT和闭环采样控制的科氏质量流量计信号处理系统*

陈 坤，郑德智，樊尚春，赵建辉

(北京航空航天大学仪器科学与光电工程学院，北京100191)

科里奥利质量流量计(Coriolis Mass Flowmeter，以下简称为科氏质量流量计，即CMF)是一种利用被测流体在振动测量管内产生与质量流量成正比的科氏力为原理制成的一种直接式质量流量仪表[1]。CMF能直接敏感被测流体的质量流量，同时可以检测流体的密度、体积流量，是一种应用广泛的新型多功能流量测量仪表[2]。

图1为典型的双U型管CMF，其振动测量管工作在谐振状态，流体在管中沿箭头方向流动。由于科氏效应(Coriolis Effect)的作用，U型管产生关于中心对称轴的一阶扭转“副振动”。该一阶扭转“副振动”相当于U型管自身的二阶弯曲振动。同时，该“副振动”与所流过的质量流量(kg/s)直接相关。因此，通过检测U型管的“合成振动”在B，B'两点的相位差就可以得到流体的质量流量[3]。因此，科氏质量流量计信号解算归根到底是两同频率正弦信号相位差的解算。

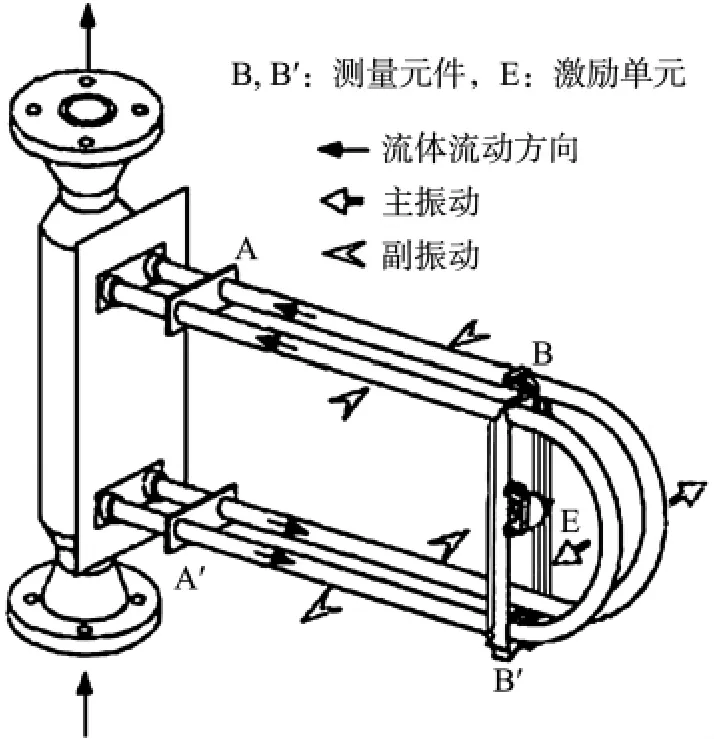
图1 CMF工作机理

传统的CMF的信号处理方式大多为采用模拟电路对两路拾振信号进行滤波和过零点检测的方法，对CMF传感器输出的两路正弦信号进行整形鉴相和高频脉冲计数的方法获得两路信号的相位差和频率[4]。但该方法需要大量使用模拟器件，噪声和干扰对测量的影响较大，并且在相位差较小时，受计数时钟精度的影响，测得相位差精度相对较低。北京航空航天大学郑德智利用数字式的相位差检测原理，采用DSP对采样后的信号进行时域分析，并采用曲线拟合的方法寻找曲线过零点，进而算出零点间的时间差和相位差。该方法对于传统的双U型管CMF精度较高，但对于新型的直管型和类直管型CMF，由于其满量程相位差微小，且工作频率较高，时间差很小，该方法已难以满足使用要求[5]。合肥工业大学徐科军参考国外的专利采用可变的采样频率进行采样，利用DSP作为二次仪表的处理核心。针对非整周期采样时的频谱泄露，采用粗测，细测和频率跟踪的思路[6]。但是该方法仅能测量出跟踪过程始末的频率变化量，对于其中的变化过程无法检测。并且由于在解算过程中是以解算结果作为控制采样率的依据，使得算法的实时性较差。在跟踪频率时，要不断变化采样频率进行采样计算，再比较功率谱值的大小，以确定实现整周期采样的频率，其时间长达10 s以上，无法满足仪表在使用上的实时性要求[7]。

1 相位差解算原理

本系统算法的核心是利用快速傅里叶变换(FFT)算法计算离散后的两路CMF信号的相位差。将CMF的输出信号理想化抽象为

在一定的条件下对输出信号进行采样，设采样周期为T，采样点数为N，则

采用离散傅里叶变换，其功率谱表达式为:

其中实部表达式为:

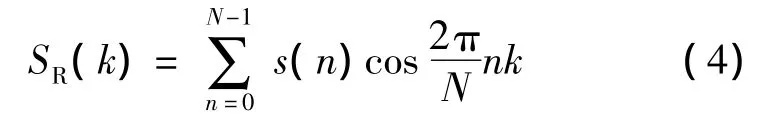
虚部表达式为:

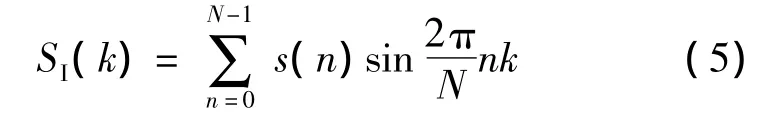
相应的幅值表达式为:

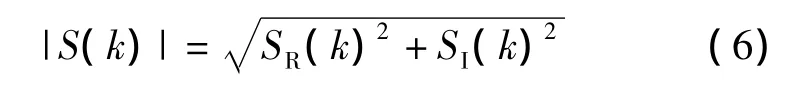
相位表达式为:

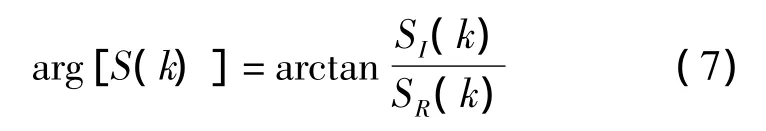
对采样数据进行处理后，进行快速傅里叶变换，找到其最大功率谱对应的k值，记为km，km对应的频率即为基波频率，从而得到相位差的表达式:

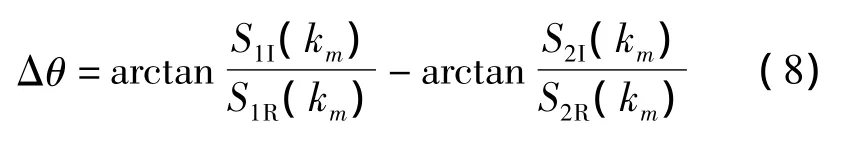
式中:S1I(km)、S1R(km)、S2I(km)、S2R(km)分别为传感器两路信号经FFT变换后其基波频率所对应的最大功率谱的虚部和实部[8]。

对于CMF输出的周期信号，要保证FFT计算基频和相位差的准确性，要求对信号进行整周期截取，并严格等时间间隔采样，否则在频域上将产生频谱泄漏误差[9]。这是由于FFT得到的频谱是离散谱线，是将信号频谱与矩形窗函数频谱作复卷积后，按归一化频率分辨率Δω=2π/N等间隔抽样的结果。如对周期信号进行整周期采样，即T0=mT。其中T0为窗函数长度，T为信号周期，m为整数。则可以得出

式(9)中f为信号频率，Δf为频率分辨率，对应于频谱图上两条谱线间的间隔。从式(9)可以看出被分析信号的频率恰好为Δf的整数倍，即正好正对某一谱线，这时计算得到的信号频率、幅值和相位将是准确的。如果进行非整周期截断，截断信号周期延拓后的新信号将不再等于原周期信号，造成信号波形的截断，这就导致信号真实频率和频率分辨率之间的比值m不再是一个整数，而是一个实数。实际上就是信号的频率将处在离散频谱的两条相邻谱线之间，而不再是正对某一谱线。这时因为频谱泄漏的影响，由谱线反映出的信号频率、幅值和相位就都存在一定的误差，不能满足测量精度要求。因此需要在软件上和硬件上进行额外的处理，使之尽量满足整周期采样的要求使频谱泄漏的影响降到最低的程度[10]。

硬件上，设计实时的频率跟踪电路，根据CMF输出信号的频率变化实时改变采样频率，保证采样频率为信号频率的整数倍，从而在最大程度上保证整周期采样的实现[11]。软件上，在进行FFT运算之前，对采样信号进行加窗函数处理。对两路信号分别加Blackman窗函数，进一步减少频率跟踪过程中的非整周期采样因素造成的频谱泄漏的影响[12]。

2 频率跟踪和闭环采样的实现

由于在CMF工作过程中由于流量的波动和外界的干扰工作频率会发生缓慢的波动，为实现整周期采样，必须进行实时的频率跟踪，准确获取信号的当前频率，并以此频率为依据控制AD采集，保证采样频率时刻为信号频率的整数倍。为此，设计如图2虚线框内所示的实现整周期采样的频率跟踪和闭环采样模块。

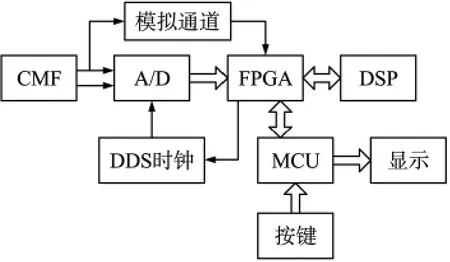
图2 系统组成

传感器输出的两路正弦信号经过模拟通道的预处理，在模拟通道内进行放大滤波和整形后，正弦信号被整形成同频率的方波信号，送入FPGA内。在FPGA内用高频脉冲对分频后的信号计数，根据计数值和计数频率就可以得到信号的当前频率。以此频率为依据，控制AD芯片以信号频率的若干整数倍的采样频率进行数字模拟量转换，保证完整信号周期内采样整数个点。利用这种方法实时地进行频率跟踪，当信号频率发生变化时，实时地改变采样频率，使得系统始终满足整周期采样的要求。

模拟数字转换电路采用音频编解码(CODEC)芯片TLV320AIC23B。该芯片能够实时同步地采集两路信号而不引入相位差，并且采样频率fs与芯片主时钟fm成比例关系，可以根据芯片主时钟灵活改变采样频率。本系统正是利用该芯片的这一特点，通过改变系统时钟频率的方式调整采样频率。其中采样频率被配置为芯片时钟频率的1/256，即fs=fm/256。系统采用DDS时钟产生电路产生AD所需的时钟信号，DDS芯片采用AD9850，其理论输出的频率分辨率为0．029 1 Hz，满足系统设计要求。由闭环控制单元FPGA控制，根据当前信号的频率产生倍频的时钟信号输出，经过比较器整形为方波时钟信号后直接驱动AD芯片进行AD采集。本系统中fclk=65 536·f0，则fs=256·f0，即控制AD芯片每周期采样256点，方便后续的FFT算法进行2N点的运算。

闭环控制由ALTERA公司的FPGA(Field Programmable Gate Array)芯片EP2C20Q240实现，内部程序由Verilog硬件描述语言编辑实现，是本系统的控制核心。一方面根据跟踪到的频率值进行计算，输出控制字驱动DDS产生相应频率的时钟输出，以实现采样频率的闭环控制;另一方面与AD采集芯片构成数据接口，将AD采集回的数据做串并转换并用乒乓操作的方式进行缓存，并与DSP进行数据通信，参与后续计算。

FPGA的硬件逻辑及外围电路实现的频率跟踪算法流程如图3所示:对传感器输出信号进行滤波后放大，运放工作于饱和状态将正弦信号整形成方波信号，送入到FPGA内部。系统时钟由75 MHz的晶振提供，在FPGA内经过PLL锁相倍频后利用150 MHz的高频时钟对分频后的方波信号进行高频脉冲计数，由计数值和计数时钟频率即可得到信号的周期值，进而可得到信号的频率。由于时钟频率较高，频率计算的分辨率较高。将当前频率锁存，待下个频率值到来时进行比较。如果频率变化范围超过设定阈值，则启动DDS输出控制模块，根据当前的频率值乘以65 536，以此为依据配置AD9850使之输出相应频率的AD时钟信号。由于采样频率为时钟频率的1/256，故采样频率即为信号频率的256倍，从而实现了整周期采样，即每周期采样256点，方便后续2N点的FFT计算，同时最大限度的减小频谱泄漏。适当设定频率控制的阈值，便可实现实时的检测信号频率的变化，依据信号频率实时改变采样频率实现采样率的闭环控制，保证了全过程整周期采样的实现。

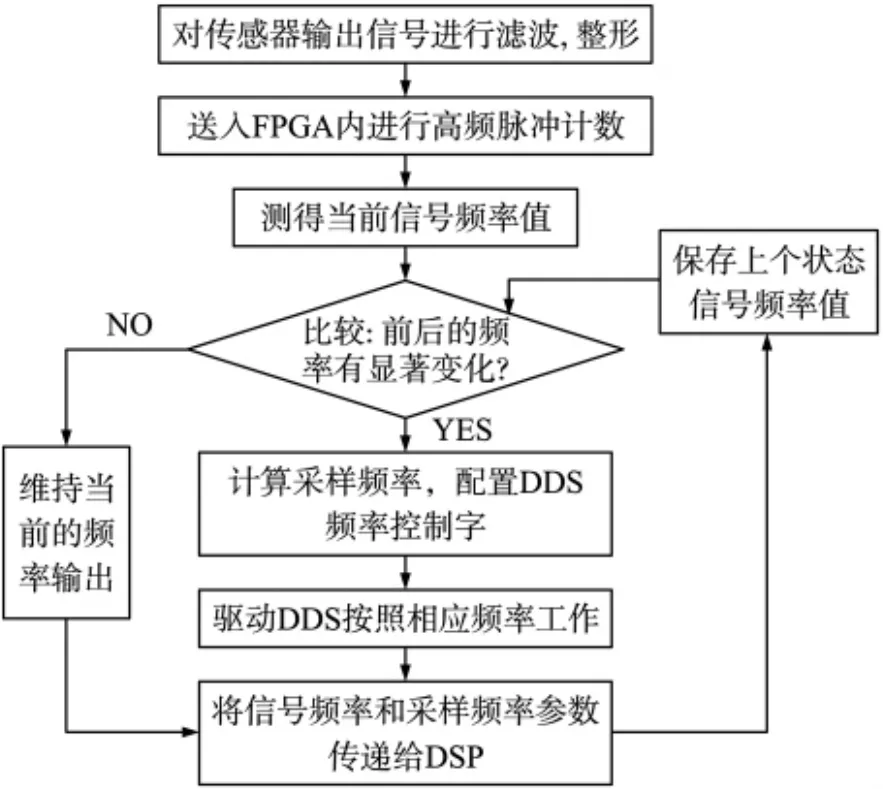
图3 频率跟踪算法流程图

3 系统实现

如图4所示，整个系统由模拟信号预处理电路，模数转换电路，频率跟踪电路，闭环控制单元及数字接口电路，数字信号处理电路，显示传输及外部接口电路等部分组成。其中频率跟踪和闭环时钟产生电路构成了闭环采样控制模块，是系统控制的核心，保证了系统整周期采样的实现，是系统算法准确实现的前提。整周期采样后的数据在FPGA内以双端口RAM(DPRAM)的形式与数字信号处理电路进行数据通信，将数据送至DSP内进行加窗函数运算和FFT运算，实时解算出CMF输出信号的相位差和时间差。数字信号处理电路采用TI的浮点型DSP芯片TMS320VC33，能够满足系统计算速度和精度的要求。解算结果经过液晶显示器显示，并能够查询累计流量等信息，提供良好的人机界面接口，系统带有10 kHz频率信号和4～20 mA电流环输出，满足工业现场的需求。显示与接口电路由单片机C8051F124控制液晶显示模块及外围接口电路实现。

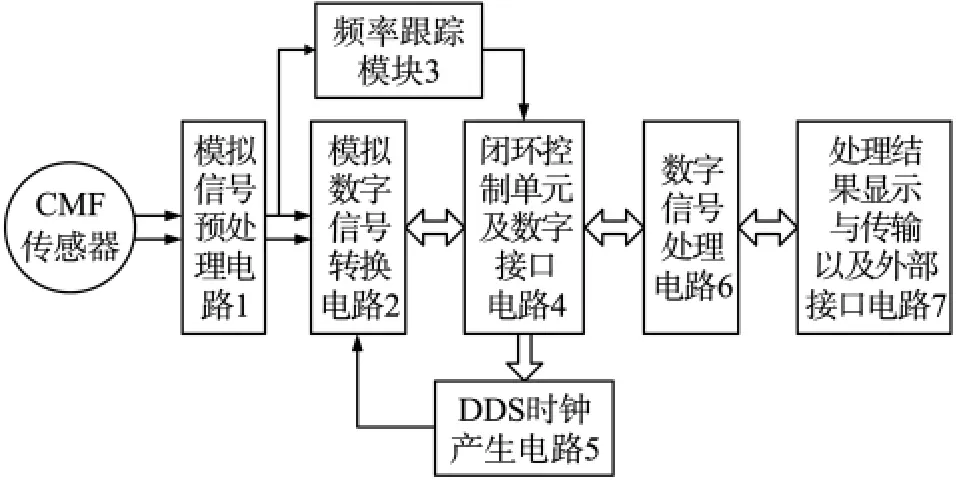
图4 系统功能模块

4 实验验证

对系统进行实验验证，利用双通道高精度信号发生器(WF1946B，相位输出精度为0．001°)产生同频正弦信号，模拟CMF传感器的输出。为准确模拟传感器的输出，加入了相对幅值为0．1的高斯白噪声。利用该系统对两路信号进行处理，解算出两路信号的相位差。由于CMF的流量与时间差成正比例关系，即Q=k*Δt，其中k为流量系数，可以通过标定得出。故直接解算出两路信号的时间差，如表1所示。考察系统解算的精度和线性度。分别选取信号频率为80～200 Hz，解算后的时间差单位为ns。

表1 时间差实验数据记录 单位:ns

分析以上数据，当设定相位差为零时，将系统解算结果作为初始相位差，并且在不同工作频率时初始相位差不相等，该初始相位差称为系统的零点误差，是由于解算系统硬件电路中的RC滤波网络引入的。由于CMF稳定工作于谐振频率下，满管和空管状态下谐振频率并没有显著差别，因此可以通过系统调零的方法减去系统零点误差，实现精确测量。对同频率的数据利用最小二乘法拟合直线，考察解算结果的线性度。在工作频率下将所有测量数据减去系统的零点误差，得到当前的绝对时间差，根据频率转换为相位差，考察解算结果的精度。结果如表2所示。

表2 计算误差及拟合偏差

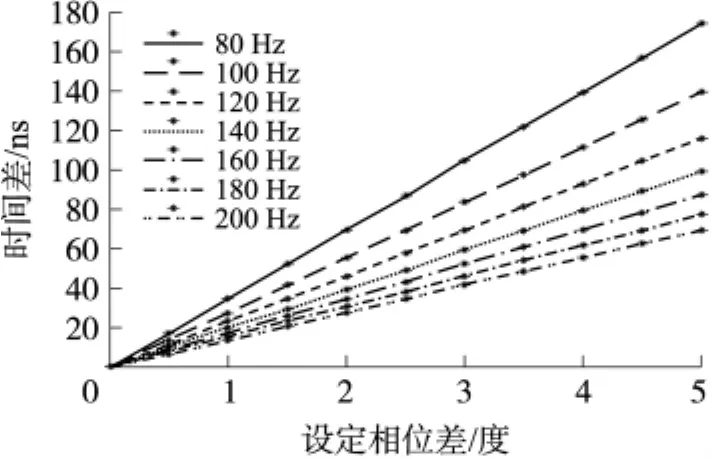
图5 实验数据拟合直线

5 结论

针对新型的直管型和类直管型CMF基频较高，满量程相位差微小的特点，在FFT算法的基础上，提出一种由硬件电路实现频率自动跟踪，实时调整AD采样率，实现采样率闭环控制的CMF信号处理系统，减小非整周期采样带来的频谱泄漏的影响，实现了实时准确的相位差解算。实验结果表明，该系统解算精度较高，测量误差小于0．1%，测量频率范围广，在新管型CMF的二次仪表中具有广阔的应用前景。

[1]Henry M P．Coriolis Meter Digital Transmitter Technology:Emerging Themes[J]．IEEE Seminar on Advanced Coriolis Mass Flow-Metering．Oxford University，2003．

[2]邢维巍，樊尚春，郑德智．科氏质量流量计数字闭环系统的设计与实现[J]．仪器仪表学报，2006，27(5):461 －465．

[3]郑德智，樊尚春，邢维巍．数字科氏质量流量计闭环系统及信号解算[J]．北京航空航天大学学报，2005．31(6):623 －626．

[4]Henry M P，Clarke D W，Vignos J H．Digital Flowmeter[P]．U．S Patent，2002．

[5]郑德智，樊尚春，邢维巍．科氏质量流量计相位差检测新方法[J]．仪器仪表学报，2005，26(5):441 －443．

[6]徐科军，于翠欣，苏建徽，等．基于DSP的科氏质量流量计信号处理系统[J]．仪器仪表学报，2002，23(2):170 －175．

[7]徐科军，姜汗科，苏建徽，等．科氏流量计信号处理中频率跟踪方法的研究[J]．计量学报，1999，20(4):304 －307．

[8]杨新华，陈玉松，金兴文．基于FFT谱分析算法的高精度相位差测量方法[J]．自动化与仪器仪表，2006年第6期．

[9]张海涛，任开春，涂亚庆．科氏质量流量计相位差的一种高精度估计方法[J]．传感器技术，2005，24(3):67 －70．

[10]杨俊，关可，梁佳．DFT变换法在科氏质量流量计相位差检测中的应用研究[J]．传感技术学报，2006，19(12):6．

[11]侯毅，施文康，迟颖．科里奥利质量流量计的原理及其误差分析[J]．自动化仪表，2001，22(9):18 －20．

[12]吴俊青．相位差的数字化测量研究[J]．应用基础与工程科学学报，2005，3:99 －104．