基于遗传EM 算法的航班延误状态空间模型

陈海燕1 王建东1 徐 涛2

(1.南京航空航天大学计算机科学与技术学院,南京,210016,中国;2.中国民航大学计算机科学与技术学院,天津,300300,中国)

INTRODUCTION

As a result of excessive demand for air transportation,the flight delay becomes an urgent problem that exacerbates national transportation bandwidth limitations.Over the past decade,researches were focused on analyzing flight delay factors,predicting delay and propagation,and mitigating delays and other issues[1-4].Deterministic models are commonly used in delay prediction.For example,one of the models is to estimate delays according to flight schedule.Models like this usually ignore random factors such as unexpected events and queuing.Prediction models based on random density functions of seasonal trends,daily propagation and daily delay[5-6],that to a certain extend reflect the overall patterns of flight delays,are insufficient in capturing variations in individual flight delay.

Real-time prediction of flight delay is essential in the state estimation process for a dynamic system.Flight operation process is monitored in order to collect data in real time,which provides an opportunity to apply dynamic data-driven application system(DDDAS)[7]that can dynamically employ prediction to control and guide the measurements,and in reverse,can dynamically steer the prediction based on the measurements.DDDAS promises more accurate analysis and prediction,more precise controls,and more reliable outcomes,which can improve advance prediction capabilities of prediction systems.The challenge in the problem remains in establishment of the delay state-space model,which is the foundation in applying the dynamic data-driven approach.P.Wang[8]presented a simple recursive model based on delay propagation. In the model,P.Wang demonstrated a linear relationship a-mong system states while ignored the effective pattern of uncertainties.In this paper,a recursive model is further improved with the use of an explicit expression to calculate flight delay caused by random factors.Delay information is feedback to the state-space model as the system input.In order to search for maximum likelihood estimates of parameters in the model,the genetic algorithm(GA)is combined with the traditional expectation-maximization(EM)algorithm to avoid the local maximum problem.Performance comparison between the model and the genetic EM algorithm is given as well.

1 STATE-SPACE MODEL OF FLIGHT DELAY

1.1 Delay propagation of flight

From departure at an airport to arrival at the destination, an aircraftaccomplishes a flight task.For efficiency and cost considerations,an aircraft should perform multiple tasks consecutively each day.Assume d denotes a departure event and a an arrival event.T hen the discrete event sequence of an aircraft performs in a day can be written as d1a1d2a2…dnan,where the state of the next event only depends on the state of the current event,and not on the state of the past event.T he discrete events sequence is a Markov chain.T herefore,the relationship among states can be represented in a state-space model.

1.2 State-space model of flight delay

The state-space model of flight delay based on the recursive model[8]can be expressed as

System model

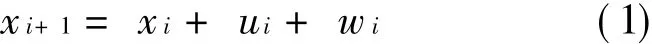
Measurement model

where xidenotes the state variable,uithe system input,yithe measurement,wiand videnote the process and measurement noise,respectively,and both are random white noises.T he system model(1)describes the evolution of the state variables over the sequence,whereas the measurement model(2)represents how measurements relate to the state variables.If an aircraft accomplish n flight tasks,then we have i=1,…,2n.When i is an odd number,xidenotes a departure delay state or an arrival delay state,vise versa.

Since the flight delay in this paper represents the difference between the actual flight time and the scheduled flight time.Random factors such as weather,baggage check-ins,and mechanical failures may result in a delayed flight.On the other hand,an early flight task completion is achievable through planning methods and strategies.Flight delays caused by these uncertainties can be added to the model as ui.Additionally,air turnaround time and ground turnaround time correspond to two uncorrelated processes.Values of uifor different models should be estimated in two delay states.However,the relationship between the uncertainties and the flight delays is not represented by any mathematical models,which leaves the calculation of uias a key problem in establishment of the state-space model.

1.3 Modeling of system input

In general,xiis the departure delay from an upstream airport,uiis represented as the delay in air.When ui＜0,it is actually denoted as flight time compensation.Earlier statistics show that the longer itinerary duration a flight is to take,the more compensation the flight can obtain.And the longer itinerary duration impacts on the final status of the arrival delay.As a result,a more effective way to represent uiis given as follows

where f sidenotes the scheduled flight time between airports,ri the delay of per scheduled flight time,or delay rate.Table 1 shows delay rates in percentage at different levels extracted from the historical flight data.

Nearly 85%of flights obtain compensation in some levels,while 15%of flights end in flight delays.T he delay rates vary significantly in distribution,decreasing sharply as a function of the distance from the center.T he statistic result suggests us to use a finite mixture model to describethe delay rate distribution.Finite mixture distribution model[9]is a mathematical method to model the generic random phenomena.Long-term empirical results show the high adaptability of this method.T he density distribution g of delay rate is modeled as a function with m mixed components.The mixture density of the ith point is written as

Table1 Percentages of delay rates at different levels

where Θ= (αi,…,αm,θ1,…,θm)denotes the parameter vector,mixing weightofthe j th component, and ψj(ri|θj)the density function of the jth component depending on parameter θj.In this paper,we assume that g is a normal mixture model.And θj is denoted as θj= (μj,∑j),where μdenotes the mean and∑the covariance matrix.

In the finite mixture model of data set r=(r1,r2,…,rn),riis assigned to the most possible component.Then,a label vector set of ri,z=(z1,z2,…,zn)is obtained.If ribelongs to the kth component,then zik=1 and the rest label variants are set to 0.Parameter vector Θ is estimated to obtain z.And the log-likelihood of Θ is given as follows

2 PARAMETER ESTIMATION BASED ON GENETIC EM ALGORITHM

The EM algorithm[10]is the most popular and effective method for parameter estimation.T he traditional EM algorithm is an iterative two-step procedure:E-step and M-step.T he E-step calculates the expectation of the log-likelihood on the observed data r and the current value of Θ.The M-step updates the corresponding estimate of Θ.After a certain number of iterations,the algorithm obtains the local optimal value of Θ.In order to avoid the local maximum problem associated with the traditional EM algorithm,calculation mechanism of GA can be applied to EM to find the global optimum.The combination of GA and EM is known as genetic EM algorithm[11].

In this paper,the fitness function used in the genetic EM algorithm is the log-likelihood function defined in Eq.(5)and calculation stops when improvement of the fitness function value decreases below a given threshold.The procedure of the genetic EM algorithm is shown as follows

3 CASESTUDYAND VALIDATION

T he flight operation data used in this case study is provided by a domestic airline.Information like arrival delay,upstream delay propagation and delay rate is extracted from the experimental data which is also divided into several groups categorized by operating date,testing set(only one set),and training set(excepting the testing set).Parameters are estimated using the genetic EM algorithm on the training set.The fitness of the model is validated on the testing set.

3.1 Density estimation of delay rate

Density estimation of delay rate is implemented in Matlab7.1.The density distribution of the original delay rate is shown in Fig.1,where the distribution represents a mixture of normal distributions rather than a single normal distribution.Assuming component number m=1,2,3,4,we obtain one single model and three mixture models after parameter estimation.As a result,Fig.2 shows a fitted distribution with two components.

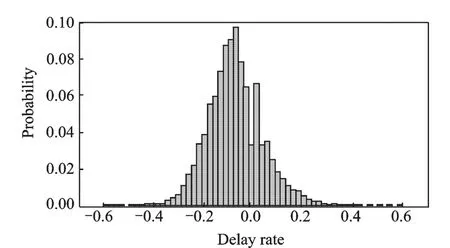
Fig.1 Density distribution of original delay rate

Fig.2 Fitted distribution with two components

3.2 Fitness test of model

Since the normal mixture models are mixtures of normal distributions,general test methods cannot be directly applied to fitness test for the model.T herefore,a hypothesis test based on Kolmogorov-Smirnov method is used in the test with steps shown as follows.

(1)Generate a number of random samples according to the density function of the mixture model,where the sample set is denoted as X1and the testing set is denoted as X2.

(2)Give a null hypothesis H0:in which X1and X2are drawn from the same continuous distribution.

(3)Run the Matlab function″(h,p)=ktest2(X1,X2)″to find whether the distributions are the same at the 5%significance level.If the significance level equals or exceeds the p-value then we have h=1,otherwise h=0.Reject H0if h=1 or accept the null hypothesis if h=0.

T he Results from all four tests on these models are listed in T able 2.The null hypothesis is accepted when m=2.Therefore,for the case study,the normal mixture model with two components has the best fitness.

Table2 Results of model tests

3.3 Performance validation of genetic EM algorithm

T he performance of model is validated in the calculation through the comparison between the genetic and the traditional EM algorithms.On the same stop criteria,the log-likelihood values produced in all iterations from the two EM algorithms with m=3 are collected and shown in Fig.3.In each step,the genetic EM algorithm achieves the better log-likelihood value,which represents the higher effectiveness.

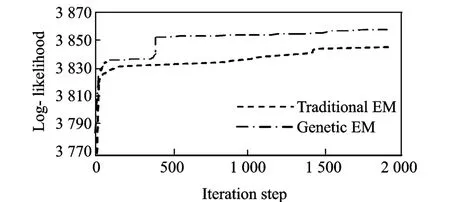
Fig.3 Log-likelihood values of genetic EM and traditional EM

Additionally,the total iteration numbers of the two EM algorithms,denoted as m,are compared in T able 3.Results show that the iteration number of traditional EM algorithm increases significantly with larger m.T he iteration number increases slightly in the genetic EM algorithm.When the algorithm preparation time is ignored,the genetic EM algorithm can achieve the faster convergence and maintain the higher accuracy than the traditional EM algorithm.

Table 3 Iteration Steps with increasing m

4 CONCLUSION

In this paper,a flight delay state-space model is proposed based on the delay propagation.In the model,delay from the upstream event is denoted as a current state,while the delay caused by other uncertainties is denoted as the system input.System inputs are produced using different models when two delay states are estimated.T he modeling process is demonstrated in detail.T he genetic EM algorithm is used to find the global optimal estimates of the parameters in the normal mixture model of random delay.Case study and model validation are carried out on real flight data.Results show that the model has an excellent fit to the real data in both the mixture density distribution calculation and the Kolmogorov-Smirnov test.In conclusion,the traditional EM algorithm can be optimized and become more efficient by using GA method in finding the global optimum.Most importantly,the flight delay state-space model proposed in this paper can make it possible to apply DDDAS to the air transportation industry in the near future.DDDAS architecture for flight delay prediction can be established based on this computational model,together with the advanced measurement infrastructure and information technology.

ACKNOWLEDGEMENT

Authors would highly appreciate the anonymous domestic airline,which provided historical flight information.

[1] Abdelghany K F,Shah S S,Raina S,et al.A model for projecting flight delays during irregular operation conditions[J].Journal of Air Transport Management,2004,10(6):385-394.

[2] Hsu C L,Hsu C C,Li H C.Flight delay propagation,allowing for behavioral response[J].International Journal of Critical Infrastructures,2007,3(3/4):301-326.

[3] Ding Jianli,Yu Yuecheng,Wang Jiandong.A model forpredicting flight delayand delaypropagation based on parallel cellular automata[C]//ISECS International Colloquium on Computing,Communication,Control and Management.Washington D C,USA:IEEE,2009:70-73.

[4] AhmadBeygi S,Cohn A,Lapp M.Decreasing airline delay propagation by re-allocating scheduled slack[J].IIE Transactions,2010,42(7):478-489.

[5] Tu Y F,Ball M,Jank W.Estimating flight departure delay distributions—A statisticalapproach with long-term trend and short-term pattern[J].Journal of the American Statistical Association,2008,103(481):112-125.

[6] Abdel-Aty M,Lee C,Bai Y Q,et al.Detecting periodic patterns of arrival delay[J].Journal of Air Transport Management,2007,13(6):355-361.

[7] Darema F.Introduction to the ICCS2007workshop on dynamic data driven applications systems[C]//International Conference on Computational Science.Berlin, Heidelberg:Springer-Verlag Press,2007:955-962.

[8] Wang P T R,Schaefer L A,Wojcik L A.Flight connections and theirimpacts on delay propagation[C]//Digital Avionics Systems Conference.Washington D C,USA:IEEE,2003,1(5.B.4):1-9.

[9] McLachlan G,Peel D.Finite mixture models[M].New York:John Wiley,2000.

[10]Dempster A,Laird N,Rubin D.Maximum likelihood from incomplete data via the EM algorithm[J].Journal of the RoyalStatisticalSociety:Series B(Methodological),1977,39(1):1-38.

[11]Pernkopf F,Bouchaffra D.Genetic-based EM algorithm for learning gaussian mixture models[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(8):1344-1348.