基于状态转移概率矩阵的轨道不平顺发展预测研究

高建敏

(西南交通大学 牵引动力国家重点实验室，成都 610031)

随着我国路网干线的全面提速和客运专线、重载运输的发展，铁路线路设备将承受更大的压力。在这种状况下，轨道状态恶化加剧，轨道不平顺发展亦加快加大。轨道不平顺的存在，一方面引起机车车辆振动和轮轨间动作用力增大，直接影响高(快)速行车的安全和平稳性;另一方面，由轨道几何不平顺状态变化引起的动荷载进一步加速轨道状态的恶化，从而限制行车速度的提高，增加线路养护维修工作量。因此，高(快)速铁路和重载铁路发展更应重视轨道的平顺性问题［1-2］。轨道不平顺是轨道实际状况的体现，研究轨道几何不平顺特征及其发展变化规律，对轨道养护维修管理具有重要意义。

然而，由于铁路线路几何状态受众多随机因素的影响而呈现出明显的随机性，决定了轨道不平顺是随里程变化的随机干扰函数［3］。因此，对轨道不平顺无法用确定性函数描述，而应当采用随机信号理论加以统计描述和分析。实际轨道运营过程中，轨检车对轨道进行定期的检查记录，形成大量的轨道不平顺检测数据。如何根据这些数据判定轨道的状态，以及跟踪轨道状态变化规律，以便合理安排养护维修工作，是轨道养护维修管理中一重要问题。日本较早认识到这一课题的重要性，开展了一系列有价值的研究［4-6］。我国开展这方面的研究较晚，开展的研究工作相对较少。何永春等［7］利用国外相关成果，对沪宁线的轨道高低不平顺进行了预测分析;许玉德等［8］利用线性预测模型，对铁路轨道质量指数(TQI)的发展进行了预测研究;陈宪麦等［9］提出了一种用于轨道不平顺发展预测的综合因子法，对轨道不平顺发展趋势进行了预测;高建敏等［10］则利用轨检车动态检测数据，分析讨论了基于不平顺分布函数的不平顺发展统计预测方法，比较了不同预测模型的预测效果和预测精度。本文在文献［10］研究基础上，引入市场活动规律分析研究中经常用到的一种预测方法——系统状态转移概率矩阵法，利用此方法，基于轨检车检测的轨道不平顺数据，建立轨道状态转移概率矩阵，预测轨道几何状态的发展变化。借此，更清晰地理解轨道几何状态的发展变化过程，使轨检车检测数据得到更充分、合理的利用，为铁路轨道几何状态管理提供参考。

1 系统状态转移概率矩阵模型

系统状态概率矩阵法是俄国学者马尔可夫创立的马尔可夫过程理论中的一个最基本的分析方法。所谓马尔可夫过程是指，如果已知系统的现在状态，则系统未来所处状态的概率性就已确定，而不管系统是如何到达现在的状态。换句话说，系统在已知现在所处状态的条件下，它将来所处的状态与过去所处的状态无关。也就是说，马尔可夫预测与决策理论是用近期资料进行预测与决策的，因而一般认为，对于某些问题，其得到的结果具有较高的可信度或准确度。

系统状态转移概率矩阵模型建立方法为，若已知系统可能存在或产生的状态数为n个，即系统状态为S1，S2，…，Sn。将系统在某个时刻 (k － 1)处于状态Sk－1，下一时刻 k转移到 Sk状态的条件概率记为 Pij，则系统状态转移情况可用矩阵表示为

转移概率矩阵用于轨道不平顺发展状态预测时，矩阵中各元素是轨道由初始分布区间转入其它分布区间或继续保留在原分布区间的概率。假定轨道状态发展恶化时，轨道不平顺元素只向着更大分布区间变化，不考虑由于其它外界因素而导致的个别元素分布区间降低的情况，则轨道不平顺状态转移概率矩阵为一下三角矩阵。矩阵对角线元素表示轨道不平顺分布区间不变，对角线以外的其它列元素表示不平顺分布向更大分布区间转移的概率。

2 轨道不平顺状态转移概率矩阵的建立

在列车动荷载反复作用下，有砟轨道不可避免地产生累积下沉，致使轨道平顺状态逐渐恶化。当道床处于稳定期时，可认为轨道累积下沉与通过总重或荷载重复作用次数间呈线性关系［11］。因此，可认为轨道不平顺随时间的变化也呈线性关系，如图1所示。当轨道不平顺状态恶化到一定程度，就必须安排养护维修，改善其大小，相应地整个轨道不平顺的分布状况也随之发生变化。故在养护维修周期内，轨道不平顺状态可看作根据当前轨道状态和轨道养护维修条件逐渐发展、恶化的过程，这同市场活动规律有某些相似之处［12］，可借鉴系统状态转移矩阵决策理论和方法，分析轨道状态的发展变化，预测未来变化趋势。

对于实测轨道不平顺数据，由于原始数据采样间隔小，数据量大，实际应用中将检测里程内数据划分为一定的单元区段，分析单元区段内轨道不平顺最大值或标准差等统计量的分布特征［6］。单元区段划分个数 N由下式确定［6］

图1 轨道不平顺状态变化

式中，L为检测线路长度;l为单元区段长度，一般根据统计要求和大型养路机械作业长度来确定。本文中采用25 m区间最大值分析轨道不平顺发展状况。

由概率论知识可知，当状态概率的理论分布未知时，若样本容量足够大，可以用样本分布近似地描述状态的理论分布。因此，对于未知分布的转移概率，可以用转移频率来近似地估计转移概率。这种情况下，系统变量由状态Sk－1转向Sk的转移概率估计值为

式中，aj为变化前处于状态Sk－1的总状态数，aij为由变化前状态 Sk－1转移到变化后状态 Sk的状态数，

将由转移频率近似估计产生转移概率形成的状态转移概率矩阵称为离散转移概率矩阵。这种由转移频率来近似估计转移概率的方法，只适合于数据量不太大和系统状态不太多的系统，如果分析系统的数据量较大，系统状态较多，则统计其转移频率就变得极为困难和复杂，这时，不便于采用这种方法来分析系统状态的变化。对于数据量较大和系统状态较多的系统，若掌握了系统状态转移概率的分布函数及其分布特征，就可以通过概率分布函数确定其转移概率，从而形成系统状态转移概率矩阵，将这种方法形成的转移概率矩阵称为连续状态转移概率矩阵。

为验证上述研究方法的可行性，以高低不平顺25 m区间最大值发展变化为例，建立了高低不平顺25 m区间最大值发展状态转移概率矩阵。原始数据为国内某干线铁路轨道不平顺动态检测数据，检测时间分别为2005年6月、7月和8月，数据采样间隔为每点0.25 m。

图2所示为选取一小段数据样本统计所得的高低不平顺25 m区间最大值离散转移概率矩阵。由图2可见，这种转移概率矩阵是极为离散的，状态转移频率或概率受原始数据影响大，转移概率矩阵不具有通用性。

轨道不平顺是随里程变化的随机函数，其分布状况及其分布变化规律是连续的，且其检测数据量是极其庞大的，不能以少量样本数据代表其总体发展变化趋势。大量研究资料表明，轨道不平顺发展近似于指数分布［4，10］，因此，类推到不平顺转移概率矩阵上，其转移概率近似具有指数分布规律。于是，可以假定转移概率Pij服从指数分布，根据指数分布规律推求轨道不平顺发展转移概率矩阵。此转移概率矩阵反映轨道不平顺总体分布趋势，不受个别异常数据影响。图3即为根据指数分布规律求出的高低不平顺25 m区间最大值发展转移概率矩阵。指数分布参数根据实际不平顺发展状况确定，本文中指数分布参数近似取值0.52。

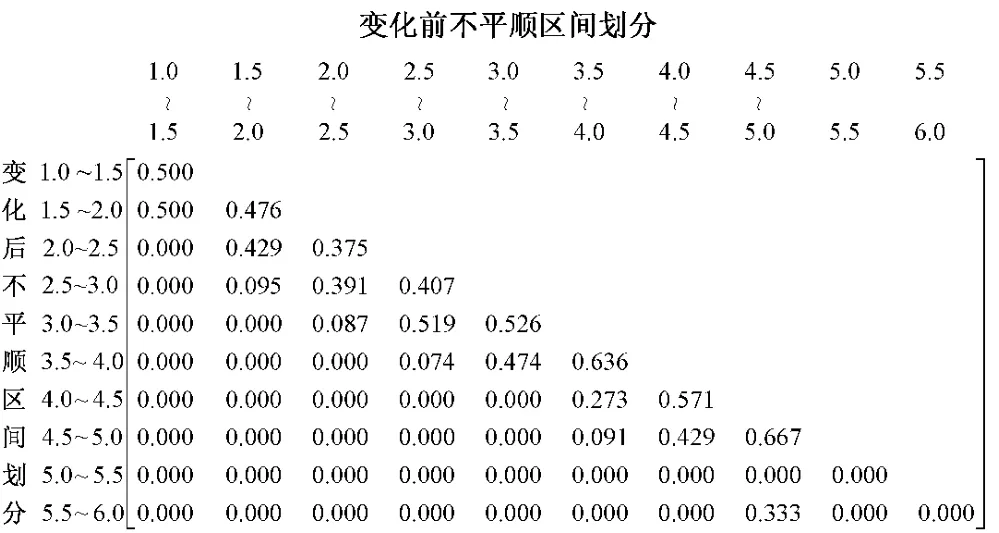
图2 轨道不平顺发展离散转移概率矩阵

图3 轨道不平顺发展连续转移概率矩阵

3 轨道不平顺状态发展预测

根据式(1)～式(5)和图2、图3所示状态转移概率矩阵，对轨道高低不平顺25 m区间最大值发展状况进行了预测。图4(a)、图4(b)分别为采用离散转移概率矩阵和连续状态转移概率矩阵，以2005年6月轨道高低不平顺25 m区间最大值分布为已知分布状态，计算所得的随后两个月不平顺区间最大值概率分布的变化情况。由图4(a)、图4(b)可以看出，无论是采用离散状态转移概率矩阵，还是采用连续状态转移概率矩阵，预测得出的高低不平顺区段最大值分布都是趋向更大的数据范围变化，说明轨道不平顺是逐渐发展和恶化的，符合轨道不平顺状态实际发展规律。由于离散状态转移概率矩阵基于小部分检测数据建立，未消除初始异常数据的影响，而连续状态转移概率矩阵基于大量轨道不平顺检测数据建立，代表更为一般的线路状况，消除了初始异常数据的影响。因此，采用连续状态转移概率矩阵预测得出的不平顺分布曲线较采用离散状态转移概率矩阵预测得出的不平顺分布曲线更光滑，分布曲线显示出的不平顺发展变化趋势更明了。

图4 轨道高低不平顺发展预测

图5、图6进一步给出了采用离散状态转移概率矩阵和连续状态转移概率矩阵预测得出的2005年7月份和2005年8月份高低不平顺区段最大值分布与根据实际检测值计算得出的分布图的对比。由图5和图6可见，无论是采用离散状态转移概率矩阵，还是采用连续状态转移概率矩阵，在短期内，轨道不平顺发展预测效果较好，但随着预测时间增长，预测效果降低。由此说明，状态转移概率矩阵法更适用于系统变化趋势的短期预测。对比图5和图6可进一步看出，由于离散状态转移概率矩阵基于小部分不平顺检测数据建立，仅对部分不平顺发展趋势进行预测，而连续状态转移概率矩阵基于大量数据样本建立，对更广泛的线路状态变化进行预测，因此，在短期内，采用离散状态转移概率矩阵的预测效果较采用连续状态转移概率矩阵的预测效果好。但是，采用连续状态转移概率矩阵预测轨道几何状态的变化，代表了更为一般的线路状况，如果能较准确地获得初期轨道不平顺分布特征及其分布参数，则采用连续状态转移概率矩阵获得的不平顺发展预测结果会更接近于实际状况。

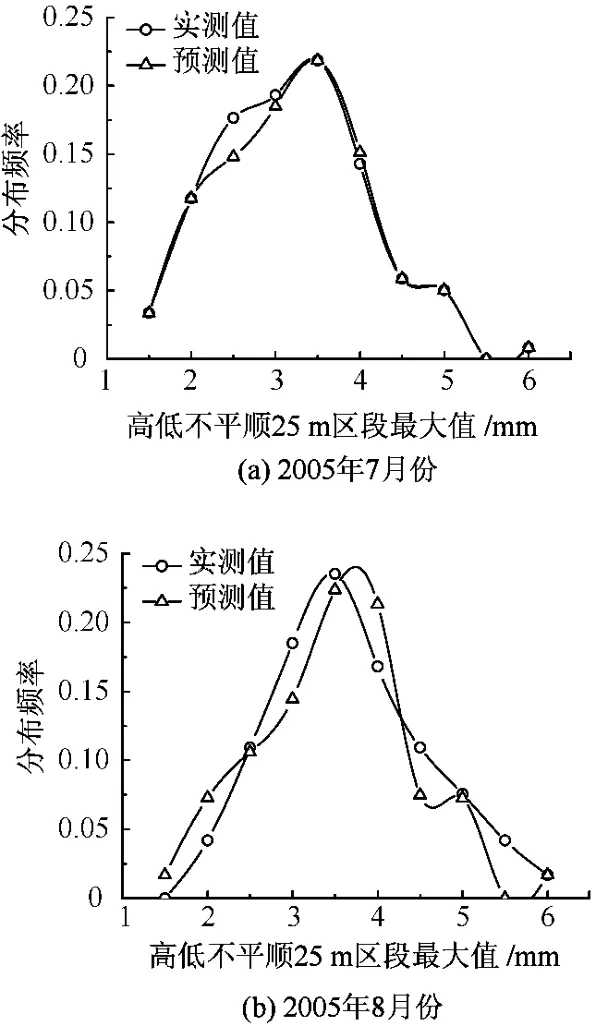
图5 高低不平顺发展实测值与预测值分布对比(离散状态转移概率矩阵)

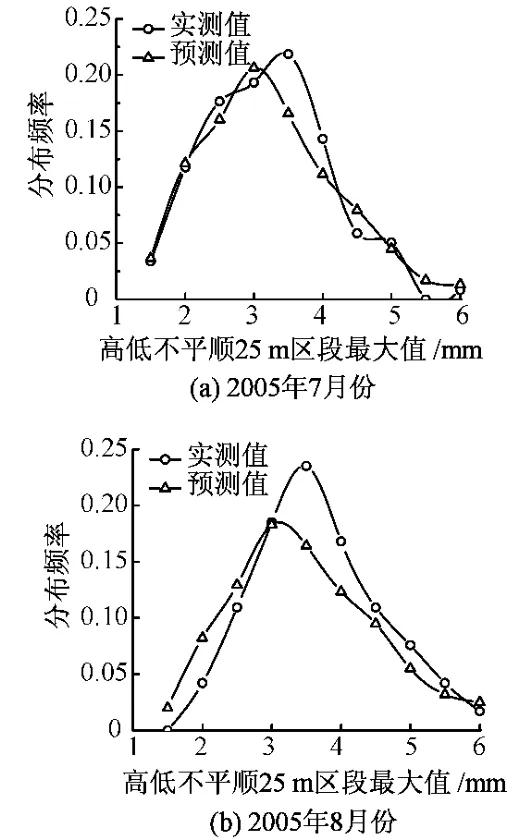
图6 高低不平顺发展实测值与预测值分布对比(连续状态转移概率矩阵)

离散状态转移概率矩阵适用于数据量小、变化状态少的系统的预测研究应用，对于像轨道不平顺检测数据这样大宗数据，直接通过频率统计手段推导离散转移概率矩阵，困难较大，不便采用。因此，需借助连续轨道状态转移概率矩阵分析不平顺分布变化趋势。上述采用连续状态转移概率矩阵预测不平顺发展的研究仅仅作为一个算例，其转移概率分布及其参数的确定仅考虑了整个轨道不平顺发展的大致情况。在实际轨道状态检测数据中，存在较多异常数据成分，这些异常数据成分在采用连续状态转移概率矩阵预测时，并不能完全再现。所以，实际应用中，应根据轨道状态实际检测情况，分析和剔除异常数据成分，较为准确地确定轨道状态发展分布特征及其主控参数。这样，才能对轨道状态变化进行更为准确、更接近实际的预测，为轨道实际状况的分析和定量把握提供一套有效的处理方法或手段。

4 结论

1)在养护维修周期内，轨道不平顺状态是一个随时间或运量逐渐发展变化的过程，轨道不平顺状态具有“重复性”或“记忆性”，新的轨道状态依赖于初始轨道平顺状态，这同市场活动规律有某些相似之处，因而，可借鉴市场活动规律分析中常用的一种工具——系统状态转移矩阵法来分析轨道几何状态变化，预测变化趋势。

2)基于轨道不平顺实测数据，以高低不平顺25 m区间最大值发展变化为例，建立了轨道几何状态发展预测的离散和连续转移概率矩阵，通过此矩阵分析了轨道几何状态的发展变化情况。结果发现，采用离散转移概率矩阵可以对轨道几何状态变化情况进行较好的预测，但是，这种转移概率矩阵只有当数据量较小、变化状态也较少时才方便建立，对于像轨道不平顺检测数据这样大宗数据，直接通过频率统计手段推导离散转移概率矩阵，困难较大，不便采用;采用连续轨道状态转移概率矩阵，可在一定程度上反映出轨道状态发展变化趋势，这种状态转移概率矩阵根据轨道不平顺发展分布特征及其分布参数确定，不受数据量限制，受异常数据影响小，方便建立，利于现场分析采用。因此，建议采用连续状态转移概率矩阵分析轨道不平顺状态的变化情况，掌握变化发展趋势，指导轨道管理工作。

3)本文只分析了轨道几何状态恶化情况，对于养护维修后，轨道状态的改善，同样可以建立轨道状态养护转移概率矩阵，分析养护维修后轨道状态的改善情况及其变化趋势。

［1］罗林.高速铁路轨道必须具有高平顺性［J］.中国铁路，2000(9):8-11.

［2］贾瑞珍，金宗斌.高速铁路线路轨道平顺问题的探讨［J］.华东交通大学学报，1997，14(3):45-48.

［3］罗林.轨道随机干扰函数［J］.中国铁道科学，1982，3(1):74-110.

［4］佐藤吉彦.新轨道力学［M］.北京:中国铁道出版社，2001:120-151.

［5］三和雅史，河西智司.数理計画モデルによる軌道狂い最適保守計画の作成［J］.鉄道総研報告，2003，17(2):35-40.

［6］许玉德.轨道不平顺预测理论及智能化决策系统的研究［D］.北京:北方交通大学，2003:60-62.

［7］何永春，王午生.铁路轨道高低不平顺的预测及其应用［J］.上海铁道大学学报，1999，2(2):64-70.

［8］许玉德，吴纪才.利用线性预测模型分析轨道不平顺发展［J］.石家庄铁道学院学报，2005，18(1):6-9.

［9］陈宪麦，王澜，杨凤春，等.用于铁路轨道不平顺预测的综合因子法［J］.中国铁道科学，2006，27(6):27-31.

［10］高建敏，翟婉明，徐涌，等.基于概率分布的轨道不平顺发展统计预测［J］.铁道科学与工程学报，2006，3(6):55-60.

［11］曾树谷.铁路散粒体道床［M］.北京:中国铁道出版社，1997:245-307.

［12］李振烈，季令.系统状态概率矩阵法在货运市场中的应用［J］.同济大学学报，2002，30(8):955-958.