大跨度上翻式拱形钢闸门振动特性及抗振优化

刘 鹏,高振海,严根华,吕飞鸣

(1.广州市水务规划勘测设计研究院,广东 广州 510640;2.南京水利科学研究院,江苏 南京 210029;3.中国水电顾问集团华东勘测设计研究院,浙江 杭州 310014)

本文以广州市荔湾区花地河南北水闸(北闸)工程[1]大跨度上翻式拱形钢闸门为研究对象。花地河南北水闸工程的功能为景观蓄水、引清调水、挡潮调蓄、补水、通航及保证泄洪安全。北闸工程采用单跨宽度达40m的液压启闭上翻式拱形钢闸门,需要适应感潮河段复杂水流条件,具有双向挡水功能,并满足局部开启防洪排涝和引水要求。闸门运行过程中存在的诸多特殊水力学和振动问题是影响工程可行性和合理性的关键技术难点。该水闸采用单孔开敞式泄水孔,净宽40m,闸室长32m。水闸总长122m,闸孔尺寸为40m×5.19 m(宽×高),底槛高程为-3m,边墩厚4 m,泄水闸宽度较大,不设检修门。水闸门叶结构见图1。

根据闸门的运行工况及水力结构特征,综合考虑闸室布置特殊、闸门孔口尺寸大、水流条件复杂等因素,需关注以下问题[2]:①局部开启排涝泄洪和引水工况下,闸门小开度时由于出闸水流的不稳定性以及水流对下游底缘的动力作用,闸门结构会出现共振现象,这对闸门结构的安全产生严重威胁;②由于水闸需要双向挡水和泄流,闸门底缘需要同时满足双向运行要求,没有现成的设计和运行经验,处理不当会造成闸门的强烈振动;③本工程采用液压启闭系统进行闸门运行操作,有别于已有类似工程的卷扬机启闭,闸门启闭杆与水平面成较小夹角,控振能力弱,此外闸门本身的振动对油缸结构的振动传递和影响也是重要研究内容。

1 闸门结构水动力荷载特性

图1 北闸泄水闸门叶结构(单位:mm)

上翻式拱形钢闸门作为重要控流结构对确保水闸的正常运行乃至整个花地河水系的安全运行具有极为重要的作用。闸门水力学试验的目标在于全面掌握闸门运行过程中的各种水力参数,论证闸门体型设计的合理性,对存在问题提出相应改善措施,以确保闸门结构的安全运行[3-5]。

1.1 上翻式拱形钢闸门水流流动特性

上翻式拱形钢闸门具有与普通闸门不同的开启方式和水流特性,开启过程闸门绕转铰转动,闸孔呈弧状,中间大、两侧小。

排水运行时,水流从闸门底缘通过,受拱形门弧线出流前沿影响,闸下两侧水流往中部汇聚,当下游水位较低时,该聚中现象尤为明显。水流聚中使闸后中部区域单宽流量加大,流速增高,如果发生水跃,则跃首下移,同时闸室两侧出现回流,该回流范围可上逆至闸门孔口处。在回流挤压下,中部主流更呈集中状,以上情况亦使孔口下游两侧水流紊动程度加重,是引发闸门小开度时强烈流激振动的振源之一。

引水运行时,拱门由正向出流变成反向出流,反拱孔口出流是发散的,当孔口边部水流撞击左右侧墙后,沿边墙水面壅高,从而形成了水面横比降,水流以略偏中的方向折向下游,该股水流加大了横向分速,对中部水流起干扰、阻挡作用,若回溯至闸门也会引起闸门振动。

闸门局部开启时,随着下游水位的上升,闸下出现自由出流、临界出流和淹没出流3种基本方式,与此相应的闸下水流衔接形式分别为自由水跃、临界水跃、临界水跃和淹没水跃。从上述流动形态观察判断,闸门下游底缘的不稳定紊乱水流将会导致闸门结构的振动,若激发闸门共振,破坏力极大,应采取措施予以解决。

1.2 工作门水流脉动压力分布特性

闸门启闭过程中受到动水作用,时均动水压力反映了水流对闸门的平均压力,而水流脉动压力则表征叠加于时均动水压力之上随时间上下波动的随机作用力。该随机作用力是诱发闸门振动的主要振源之一,也是判断闸门结构体型优劣的重要依据[5-6]。该闸门门型新颖,结构跨度大,门下出流流态复杂,水跃、波浪对门体冲击引起的压力脉动是诱发闸门强烈振动的基本振源。此外下泄水流对底缘的不稳定作用亦是导致闸门强烈振动的振源之一。

鉴于闸孔为圆弧形孔口出流,闸中部和闸边部差异较大,试验共选取闸门中心线断面、闸门边断面和闸门1/4断面进行脉动压力测量。测试结果表明:作用于门体上的脉动压力具有随开度、泄量的增大而增大的变化规律。底缘部位脉动压力最大,正常情况下最大脉动压力均方根值为1.287 kPa,这种压力大脉动现象系门后水流旋滚所导致。排水工况正常运行时典型测点脉动压力时域过程见图2。水流脉动压力自底缘由下而上呈下降趋势。作用于门体的脉动压力的主能量集中在f=0～10Hz范围,其中优势频率集中在5Hz以内。当闸门发生强烈振动时作用于门体的脉动压力出现谐波现象(图3),共振水流脉动频率约为2.9Hz。

图2 排水工况正常运行时典型测点P13脉动压力时域过程

2 闸门结构流固耦合动力特性

2.1 流固耦合基本理论

当闸门处于水中时,闸门的振动必然引起水体压力的波动,水体压力波动又会影响闸门的振动,这是一个典型的液体和弹性体的耦合振动问题[7]。流固耦合振动自振特性方程[3]可表示为

图3 排水工况发生共振时典型测点P13脉动压力时域过程

式中物理量符号含义见文献[3]。式(1)比单个固体振动方程多了一个动水压力向量P。P采用无黏性不可压缩的微幅流体运动方程确定。扰动压强p满足拉普拉斯方程:

引入 Φ(x,y,z,t)为水流扰动速度势,由流体的连续性方程知,Φ亦满足拉普拉斯方程:

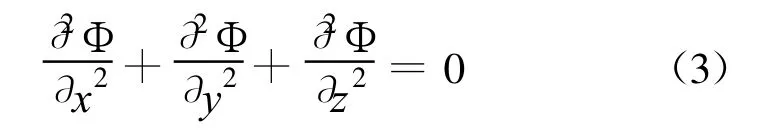
而p及Φ之间的关系为

考虑流体作用面与水接触面等边界条件,如

式中:n表示法向坐标;﹒δn为法向速度。

此外,远处水流的扰动速度和扰动压强均应趋近于零。流体作用面表面法向速度与水质点的法向速度应相等,即

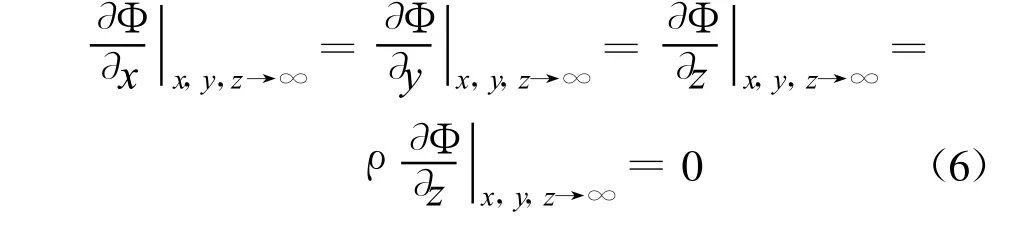
式(2)～(4)为扰动水压力控制方程组,流体作用面与水接触节点上的动水压力向量 P f可表示为其表面节点加速度 ¨δf的线性组合,即

式中:D为系数矩阵。

P与Pf具有不同数量的项次,为此引入转换矩阵S:

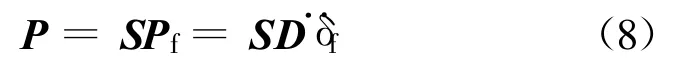
再引入 δ与δf之间的转换阵 T,则

式中:Mp就是通常所称的附加质量阵。

式(11)为在水介质下的结构自由振动的耦合控制方程,可转化为如下形式的特征值问题:

此处Mp是非对称矩阵,因此不能将其转化为标准特征值问题。用于求解非对称特征值问题的方法是Lanczos法。

2.2 有限元模型分析

闸门结构的动力特性主要包含结构固有频率、振型等参数,考虑到工程实际运行时闸门受到动水作用而振动,流场对结构固有特性将起到显著影响,因此动力分析时必须考虑水介质对结构动力特性的影响[7]。

上翻式拱形钢闸门工作状态下孔口宽度为40.0m,门高为 5.19 m。采用 shell63壳单元和beam88梁单元对结构联合建模。分析软件为ANSYS,有限元模型共包括3432个面,35839个节点,37477个shell板壳单元,532个beam4梁单元,共有215034个自由度。考虑启闭机油缸后,总质量为167.29 t。在位于启闭油缸固定端、油缸和吊耳梁连接部位以及支铰部位均释放其绕 x轴转动自由度。门前流场长度取10倍门高,以保证流固耦合计算精度。在流固耦合条件下,闸门前3阶固有频率分别为2.11Hz,2.75Hz和3.97Hz,分别反映闸门面板中上部径向弯曲变形振动模态、闸门两侧面板上下部径向弯曲变形振动模态(图4)。总体上说,闸门振动频率较低,这是由大跨度、低刚度闸门的结构特性所决定的。

3 闸门结构流激振动特性

水工闸门是水利枢纽的控制结构,其使用过程中的振动是影响结构稳定性及其强度的主要因素,由于流固耦合的复杂性,很难通过理论计算获得振动精确解[8]。

3.1 水弹性模型的设计

图4 闸门流固耦合典型振型

上翻式拱形钢的基本物理力学指标为:密度7.85×103kg/m3、弹性模量 2.10×105MPa、泊松比0.3,选定的水弹性模型几何比尺Lr=20。水弹性模型材料按水弹性相似原理设计,其基本物理力学指标为:密度 7.85×103kg/m3、弹性模量 1.05×104MPa、泊松比0.3。目前市场上没有同时满足上述参数的型材,因此试验采用的材料为特别研制的特种水弹性材料。该材料使用重金属粉、高分子材料等进行多组分特种材料研制,并运用专用模具特制适合本工程使用的型材。测试结果表明:选用的水弹性材料基本达到模型密度ρm=ρp(ρp为原型密度)、结构弹性模量 Er=Lr的要求。

3.2 原方案闸门振动特征

闸门振动加速度测量数据的处理采用随机振动理论及其谱分析方法进行,分别获得闸门振动过程的谱特征和数字特征,揭示闸门振动的频域能量分布及振动量级。

试验在闸门开度为0～2.6m(拱形闸门中点开度)时分排水及引水2种工况进行。结果表明,在内涌水位0.80m、外江水位-0.50m的排水工况下,闸门开度在1.0m以上时闸门结构运行相对平稳,振动量级不大(图5);但闸门开度在0.1～1.0m的较大区间内,由于下泄水流漩滚区间位于闸门底缘附近,或虽形成淹没出流但水流脉动能量较大,易激发共振,一旦激发共振振动量级成数十甚至更高的幅度迅速递增,从而导致闸门结构破坏。闸门3个方向的振动加速度存在如下关系:az＞ay＞ax。各运行工况下闸门结构振动加速度最大均方根值分别为:顺水流方向(x方向)为0.359 m/s2、垂直水流方向(y方向)为 0.602m/s2、铅直方向(z方向)为1.361 m/s2。从频谱分析(图6)可以看出闸门共振激发区的共振频率为2.9Hz,与共振状态水流脉动压力主频一致。闸门结构最大振动应力均方根值分别为:外面板10.731MPa、内面板24.11 MPa、横梁翼缘板50.72MPa、纵梁翼缘板为33.36MPa、横梁腹板为7.78MPa、纵梁腹板为10.05mPa、吊耳外翼板为14.07MPa、吊耳内翼板为5.25MPa。

图5 排水工况正常运行时典型测点振动加速度及功率谱密度

图6 排水工况发生共振时典型测点振动加速度时域过程及功率谱密度

引水工况时闸门结构振动量级随开度的增大逐渐增加,但总体振动量级不大。试验测得不同工况下闸门结构最大振动加速度均方根值分别为:顺水流方向为0.044 m/s2、垂直水流方向为0.048 m/s2、铅直方向为0.047m/s2。结构最大振动应力均方根值为3.043MPa。

4 闸门结构抗振优化设计

鉴于上翻式拱形钢闸门原设计方案在排水工况下容易产生强烈共振,为确保工程安全,需对闸门结构进行抗振优化设计。

4.1 闸门优化布置方案

根据水动力试验结果,针对诱发闸门结构产生强烈振动的原因,拟定5个修改方案进行可行性比较研究。优化方案重点针对闸门底缘结构进行修改调整,以改善水流流态,抑制共振的发生。

诸修改方案特点如下:①方案Ⅰ在保持闸门结构原设计形式不变的基础上,在下节浮箱内侧按间隔1500mm开直径为300mm的圆孔,旨在消除下节浮箱效应,从而减小运行过程中的闸门浮力,减小闸门振动量级。②方案Ⅱ在方案Ⅰ的基础上,将闸门结构下节浮箱封板改成宽为500mm的翼缘板,并将闸门结构底部横梁及上节浮箱内腹板各开1个直径为300mm的圆孔,旨在减小闸门底缘水流的顶托力,消除闸门浮箱影响,从而减小运行过程中的闸门浮力,减小闸门振动量级。③方案Ⅲ将闸门止水移至闸门底缘中部,减小闸门下游倾斜面水平面投影面积,从而降低闸门底缘的顶托力,以减小闸门振动量级。④方案Ⅳ在方案Ⅲ的基础上,移动底缘位置,并将闸门止水底部小横梁尺寸缩小,并在内侧底封板、底横梁、上节浮箱内封板开孔(直径为300mm),以消除闸门浮箱影响,减小闸门浮力,从而减小闸门振动量级。⑤方案Ⅴ闸门形式基本同方案Ⅲ,将闸门止水移至闸门底缘中部,并进一步向外江侧偏移,竖板中心距外弧板661mm,距内弧板339mm,闸门底部小横梁长度改为40mm。为减小引、排水工况时的底缘顶托压力脉动荷载,将外江侧底缘改为梁格结构,同时在上节浮箱外江侧开直径为500mm的进人孔,上下横梁分别开直径为200mm和100mm的透水孔,从而减小闸门振动量级。典型闸门底缘体型修改方案见图7。

4.2 闸门优化布置试验结果

方案Ⅰ、方案Ⅱ在保持闸门结构原设计形式不变的基础上,通过在下节浮箱内侧及横梁开孔,消除下节浮箱密封性,从而减小运行过程中的闸门浮力,改善压力分布,削减闸门底缘顶托力,以达到减小闸门振动量级的作用。试验结果表明闸门优化方向是正确的,大范围减小了闸门共振区间及共振量,但排水工况下仍有部分区间会发生一定量级的闸门共振。

方案Ⅲ、方案Ⅳ将闸门止水移至闸门底缘中部,通过减小闸门下游倾斜面水平面投影面积及浮箱空间等措施来降低闸门底缘的顶托力,减小闸门浮力,从而减小闸门振动量级。试验结果表明闸门优化方向是正确的,避免了排水工况的闸门共振现象,减小了闸门振动量级,但在引水工况下发生了低频微弱谐振现象,且内涌水位越低,谐振量级越大。

方案Ⅴ在方案Ⅲ的基础上,通过调整闸门底缘的倾斜度和倾斜面所占比例,缩减闸门底部小横梁尺寸,在闸门浮箱位置开设进人孔、透水孔以减小谐振量级,试验表明该项措施较好地起到了减小闸门振动量级、抑制结构谐振的效果,且可通过水闸运行操作管理彻底避免谐振产生,能确保闸门结构的安全运行。

图7 典型闸门底缘体型修改方案(单位:mm)

综合考虑多种优化方案的试验成果,依照设计运行工况范围,拟推荐方案Ⅴ供设计部门选用。不同测点推荐方案排水工况闸门结构振动加速度随开度的变化关系见图8。

图8 不同测点推荐方案排水工况闸门结构振动加速度随开度的变化关系

5 结 论

a.上翻式拱形钢闸门属大跨度低刚度结构,系统固有频率低,若体型布置不当,在水动力荷载作用下容易诱发共振,其振型以垂向和径向为主。一旦发生共振,振幅很大,闸门容易遭受损坏,因此闸门的抗振体型研究显得极为重要。

b.闸门结构的流固耦合动力分析取得了闸门的固有频率和振型等模态参数,前3阶固有频率在2.11～3.97Hz范围变化,为结构共振分析提供了依据。

c.闸门水动力荷载测试数据显示,闸门结构一旦发生强烈共振现象,作用于闸门的水流脉动压力出现谐波现象,其脉动频率与结构共振频率一致,约为2.9Hz,该水流脉动频率落入结构前3阶固有频率区,构成闸门共振的基本条件。

d.通过水弹性振动模型的研制和开发,系统试验研究了闸门在排水和引水2种工况下的动力响应特征,正确反演了流激振动响应特征和闸门共振现象,为结构的抗振优化修改奠定了基础。

e.闸门结构的抗振优化重点针对底缘体型修改进行,推荐方案消除了闸门强烈振动的现象,闸门运行平稳,无共振现象,取得了显著的抗振效果。

[1]广州市水利水电勘测设计研究院.广州市荔湾区花地河南北水闸(北闸)工程初步设计报告[R].广州:广州市水利水电勘测设计研究院,2009.

[2]南京水利科学研究院.广州市荔湾区花地河北闸闸门水弹性振动试验研究[R].南京:南京水利科学研究院,2010.

[3]严根华.我国大跨度闸门应用趋势与抗振对策[J].水利水运工程学报,2009(4):134-142.

[4]严根华.水动力荷载与闸门振动[J].水利水运工程学报,2001(2):10-15.

[5]YAN Gen-hua.Experiments and researches on flow-induced vibration of large radialworking gate in sand sluicing chamber[C]//Proceedings of 16th IAHR-APD Congress and 3rd Symposium of IAHR-I SHS Advance in Water Resources and Hydraulic Engineering.Nanjing:IAHR,2008.

[6]DL/T 5039—1995 水利水电工程钢闸门设计规范[S].

[7]古华,严根华.水工闸门流固耦合自振特性数值分析研究[J].振动测试与诊断,2008(3):242-246.

[8]严根华.水工闸门流激振动研究进展[J].水利水运工程学报,2006(1):66-73.

[9]罗银森,刘佑清,吕飞鸣.苏州河河口水闸流体激振模型试验[J].水利水电科技进展,2007,27(S1):101-104.

[10]潘锦江.闸门振动问题探讨[J].水利水电科技进展,2001,21(6):36-39.